Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Уравнения Максвелла
Содержание
- 1. Уравнения Максвелла
- 2. Общая физика. «Электромагнитная индукция»ЯВЛЕНИЕ САМОИНДУКЦИИ. ИНДУКТИВНОСТЬ
- 3. Общая физика. «Уравнения Максвелла»ЭНЕРГИЯ МАГНИТНОГО ПОЛЯЭнергия
- 4. Общая физика. «Уравнения Максвелла»Изменяющееся во времени
- 5. Общая физика. «Уравнения Максвелла»Итог:
- 6. Общая физика. «Уравнения Максвелла»(поменяли местами операции дифференцирования и интегрирования).Сведения из теории электростатического поля.
- 7. Общая физика. «Уравнения Максвелла»
- 8. Общая физика. «Уравнения Максвелла»Общий вывод:
- 9. Общая физика. «Уравнения Максвелла»Единая теория электрических
- 10. Общая физика. «Уравнения Максвелла»Рассмотрим цепь переменного
- 11. Общая физика. «Уравнения Максвелла»ГВыберем контур Г, охватывающий подводящий провод, зададим направление обхода контура.
- 12. Общая физика. «Уравнения Максвелла»Поверхность S1 пересекает
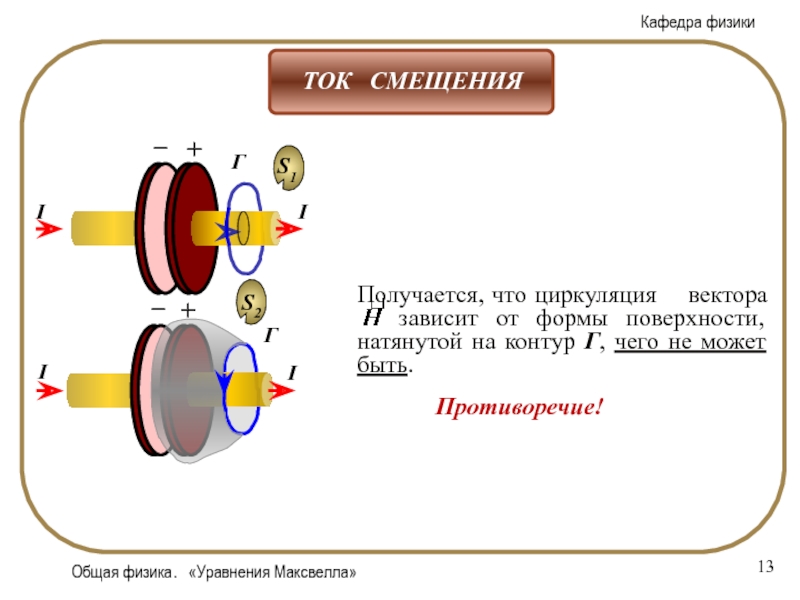
- 13. Общая физика. «Уравнения Максвелла»Противоречие!
- 14. Общая физика. «Уравнения Максвелла»Сумма токов проводимости
- 15. Общая физика. «Уравнения Максвелла»В основе теории
- 16. Общая физика. «Уравнения Максвелла»Уравнения Максвелла.1.Уравнение показывает,
- 17. Общая физика. «Уравнения Максвелла»2.Поток вектора индукции
- 18. Общая физика. «Уравнения Максвелла»3.Под полным током
- 19. Общая физика. «Уравнения Максвелла»4.Поток вектора электрического
- 20. Общая физика. «Уравнения Максвелла»Из уравнений Максвелла
- 21. Скачать презентанцию
Общая физика. «Электромагнитная индукция»ЯВЛЕНИЕ САМОИНДУКЦИИ. ИНДУКТИВНОСТЬ Электромагнитная индукция возникает при изменении магнитного потока через контур. Если в контуре течет изменяющийся во времени ток, то магнитное поле этого тока также будет
Слайды и текст этой презентации
Слайд 1Общая физика. «Электромагнитная индукция»
9 апреля 2013г.
ЛЕКЦИЯ 9.
ПЛАН ЛЕКЦИИ
Явление самоиндукции.
Индуктивность.
Максвелла.
Слайд 2Общая физика. «Электромагнитная индукция»
ЯВЛЕНИЕ САМОИНДУКЦИИ. ИНДУКТИВНОСТЬ
Электромагнитная индукция возникает
при изменении магнитного потока через контур. Если в контуре течет
изменяющийся во времени ток, то магнитное поле этого тока также будет изменяться. Следовательно, появится ЭДС индукции в этом же контуре. Это самоиндукция.Далее - самостоятельно!
Слайд 3Общая физика. «Уравнения Максвелла»
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Энергия локализована в возбуждаемом
током магнитном поле. Это магнитная энергия тока или собственная энергия
тока.Далее - самостоятельно!
Слайд 4Общая физика. «Уравнения Максвелла»
Изменяющееся во времени магнитное поле вызывает
появление в контуре сторонних сил, действующих на носители тока. Максвелл:
переменное магнитное поле порождает электрическое поле. В итоге в неподвижном контуре возникает индукционный ток. Это вихревое поле.Свойства вихревого электрического поля.
Воспользуемся определением ЭДС. Для электростатического поля ЭДС это циркуляция вектора напряженности поля по замкнутому контуру:
Слайд 6Общая физика. «Уравнения Максвелла»
(поменяли местами операции дифференцирования и интегрирования).
Сведения
из теории электростатического поля.
Слайд 9Общая физика. «Уравнения Максвелла»
Единая теория электрических и магнитных явлений
создана Максвеллом. Основа теории - идея Максвелла о симметрии во
взаимозависимости электрического и магнитного полей.Для создания теории Максвелл ввел в рассмотрение ток смещения.
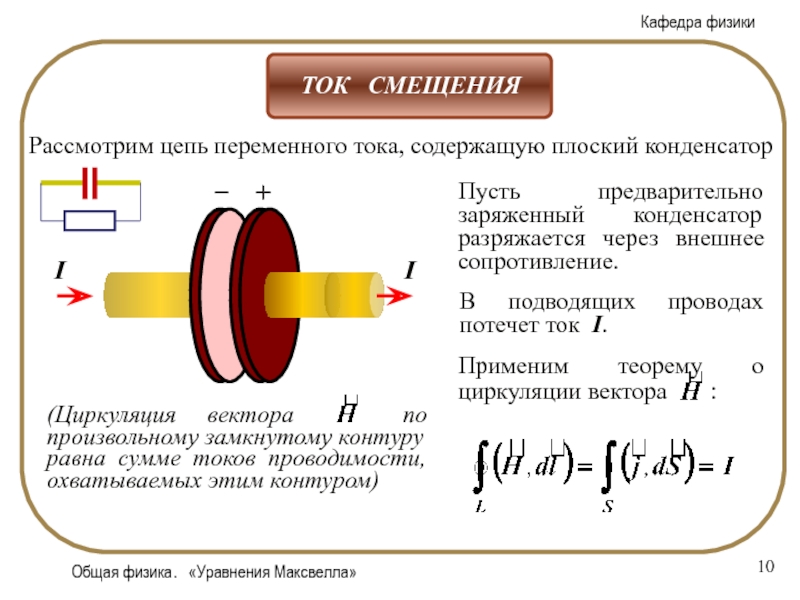
Слайд 10Общая физика. «Уравнения Максвелла»
Рассмотрим цепь переменного тока, содержащую плоский
конденсатор
+
–
I
I
Пусть предварительно заряженный конденсатор разряжается через внешнее сопротивление.
В
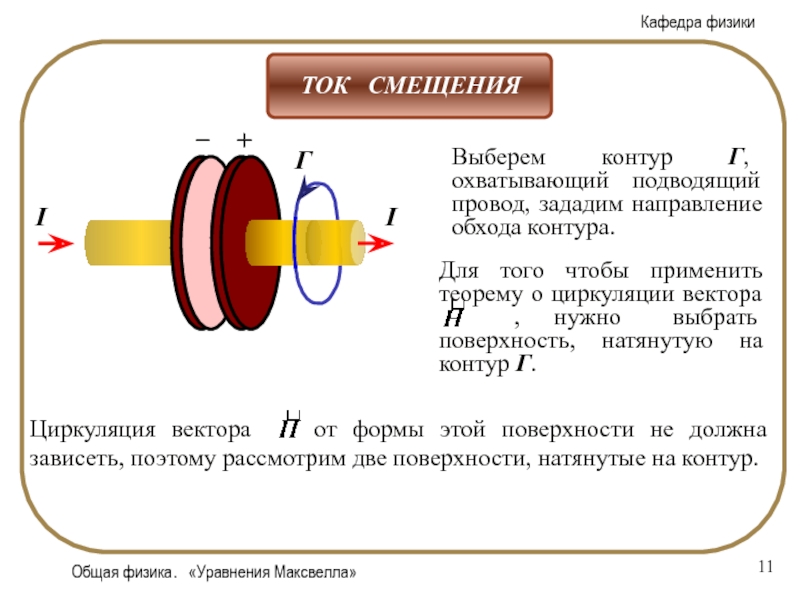
подводящих проводах потечет ток I. 
Слайд 11Общая физика. «Уравнения Максвелла»
Г
Выберем контур Г, охватывающий подводящий провод,
зададим направление обхода контура.
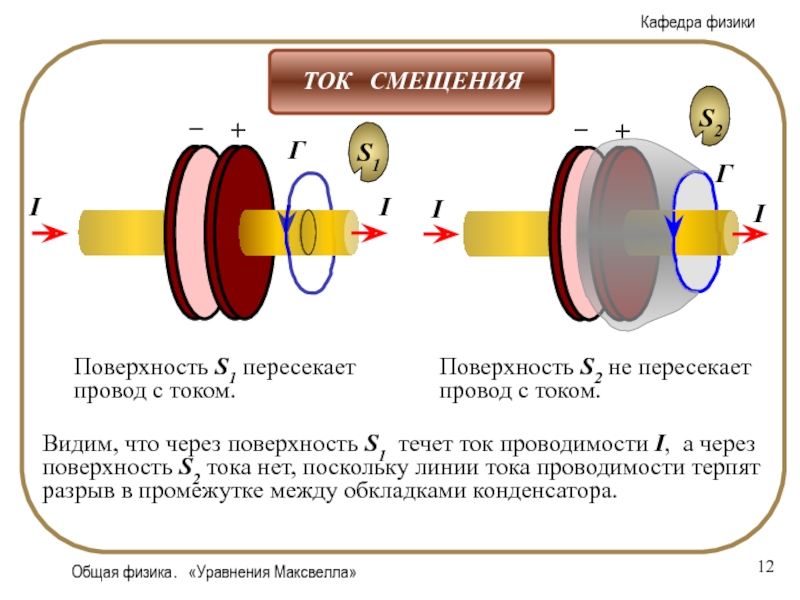
Слайд 12Общая физика. «Уравнения Максвелла»
Поверхность S1 пересекает провод с током.
Поверхность S2 не пересекает провод с током.
Видим, что через
поверхность S1 течет ток проводимости I, а через поверхность S2 тока нет, поскольку линии тока проводимости терпят разрыв в промежутке между обкладками конденсатора. 
Слайд 14Общая физика. «Уравнения Максвелла»
Сумма токов проводимости и смещения -
полный ток:
Плотность полного тока:
Для разрешения противоречия Максвелл ввел понятие о
плотности тока смещения. Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости в конденсаторе замыкаются токами смещения.
Слайд 15Общая физика. «Уравнения Максвелла»
В основе теории - четыре уравнения.
В учении об электромагнетизме эти уравнения играют такую же роль,
как законы Ньютона в механике.Открытие тока смещения позволило Максвеллу создать единую теорию электрических и магнитных явлений – макроскопическую теорию электромагнитного поля.
Термин «ток смещения» - условный. По существу, это изменяющееся со временем электрическое поле.
Общий вид теоремы:
Слайд 16Общая физика. «Уравнения Максвелла»
Уравнения Максвелла.
1.
Уравнение показывает, что источником электрического
поля могут быть не только электрические заряды, но и изменяющиеся
во времени магнитные поля.
Слайд 17Общая физика. «Уравнения Максвелла»
2.
Поток вектора индукции магнитного поля через
произвольную замкнутую поверхность равен нулю.
Магнитное поле не имеет стоков и
истоков, линии поля не имеют ни начала ни конца. Магнитное поле называют соленоидальным или вихревым.Это теорема Гаусса для магнитного поля.
Уравнения Максвелла.
Слайд 18Общая физика. «Уравнения Максвелла»
3.
Под полным током понимается сумма токов
проводимости и смещения. Уравнение показывает, что магнитные поля могут возбуждаться
либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.Уравнения Максвелла.
Слайд 19Общая физика. «Уравнения Максвелла»
4.
Поток вектора электрического смещения через произвольную
замкнутую поверхность в произвольной среде равен стороннему заряду, заключенному внутри
поверхности.Уравнения Максвелла.
Слайд 20Общая физика. «Уравнения Максвелла»
Из уравнений Максвелла следует:
- источниками электрического поля являются электрические заряды, либо изменяющиеся во
времени магнитные поля.- источниками магнитного поля являются движущиеся заряды (электрические токи), либо переменные электрические токи.
Уравнения Максвелла не симметричны относительно магнитных и электрических полей. Причина: в природе существуют электрические заряды, но не обнаружены заряды магнитные.
