Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Содержание
- 1. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
- 2. Математическая статистика - это раздел
- 3. Вариационные ряды и их характеристики
- 4. Пусть требуется изучить некоторую совокупность объектов относительно
- 5.
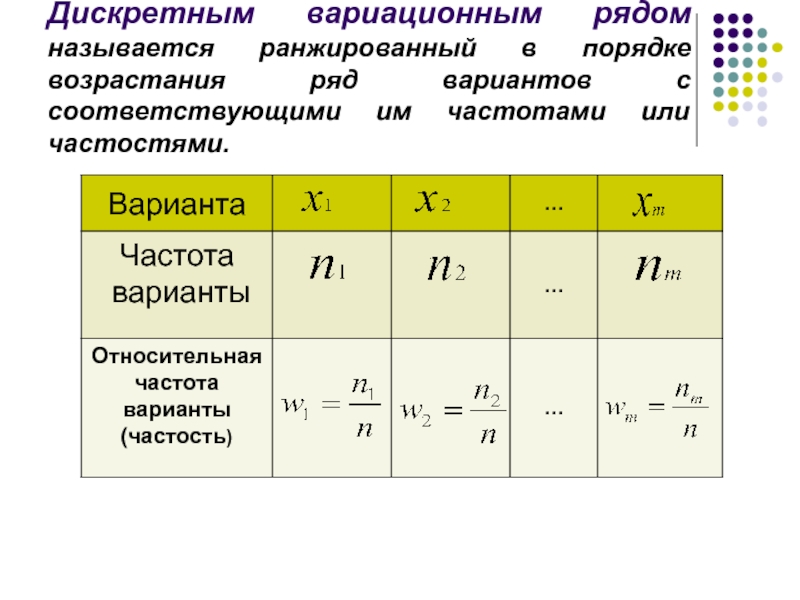
- 6. Дискретным вариационным рядом называется ранжированный в порядке возрастания ряд вариантов с соответствующими им частотами или частостями.
- 7. Пример. 20 студентов на экзамене по психологии
- 8. Дискретный вариационный ряд:
- 9. Пример. Имеются данные о заработной плате сотрудников
- 10. Если число различных значений признака в выборке
- 11. Интервальный вариационный ряд
- 12. Слайд 12
- 13. Графическое изображение вариационных рядов
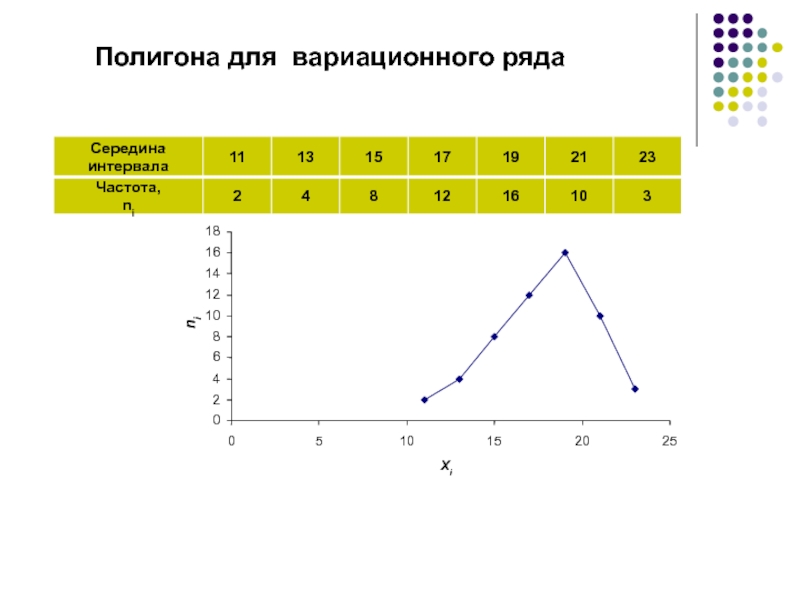
- 14. Полигоном частот (относительных частот) интервального ряда называется
- 15. Полигона для вариационного ряда
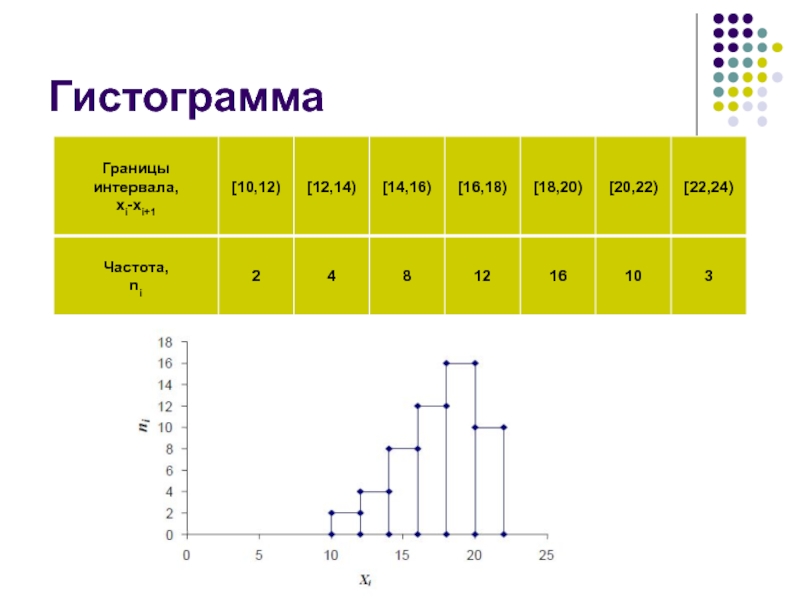
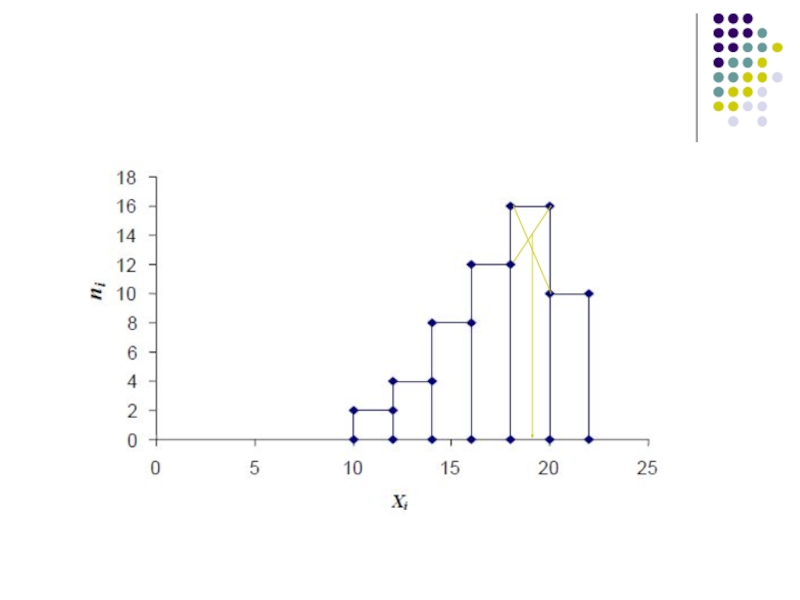
- 16. Гистограмма Применяется
- 17. Гистограмма
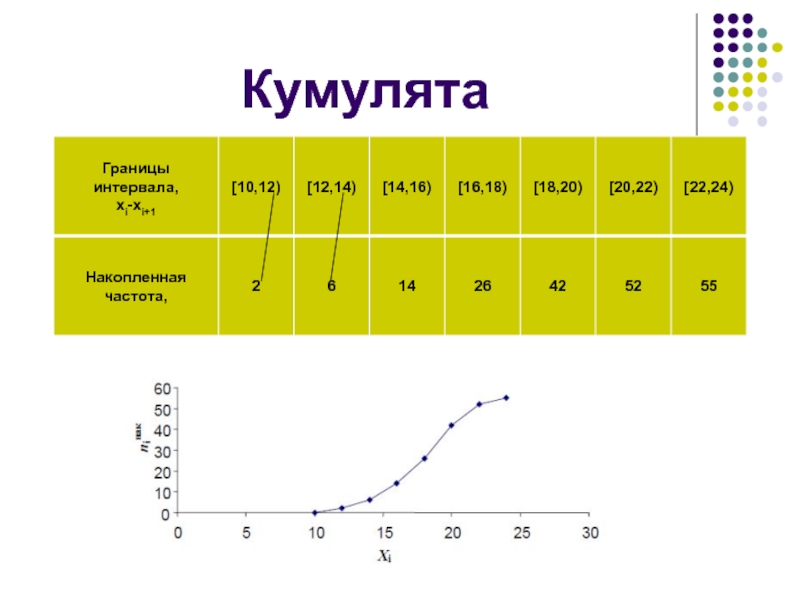
- 18. КумулятаКумулятивная кривая (кумулята) – кривая накопленных частот.
- 19. Кумулята
- 20. Числовые характеристики вариационного ряда: Средние величины Показатели вариации
- 21. Средние величиныСредние величины характеризуют значение признака, вокруг
- 22. Средней арифметической вариационного ряда называется сумма произведений
- 23. Мода (Mo) - это значение, которое
- 24. Слайд 24
- 25. Моду можно найти по формуле
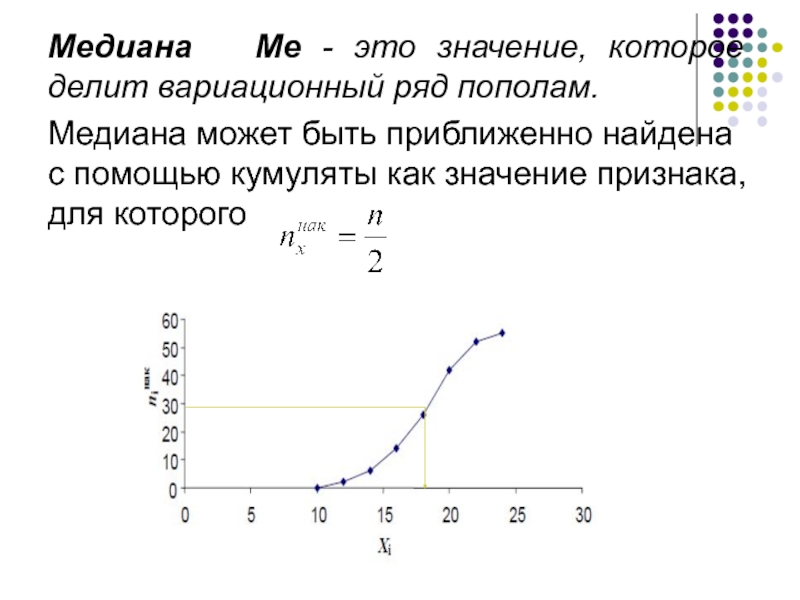
- 26. Медиана Me - это значение, которое
- 27. Медиану можно найти по формуле
- 28. Показатели вариацииДисперсией вариационного ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:Среднее квадратическое отклонение
- 29. Показатели вариации
- 30. Показатели вариации
- 31. Показатели вариации
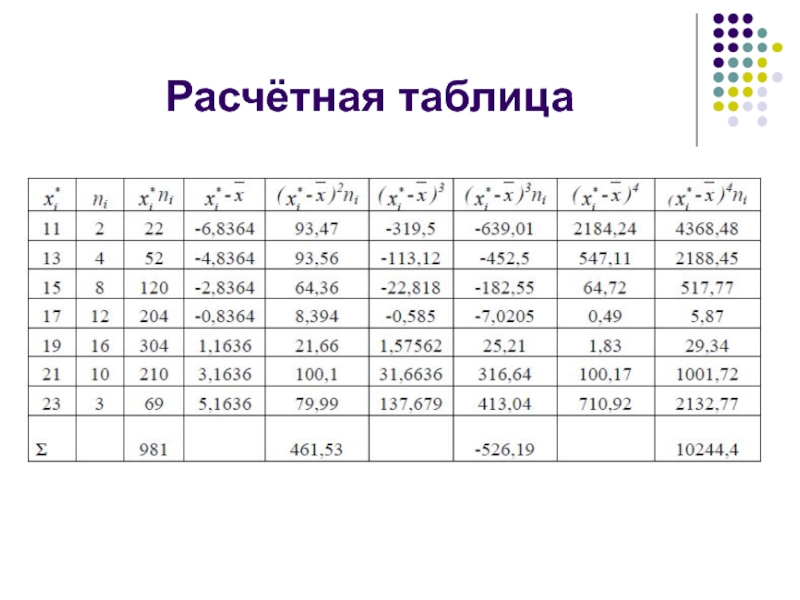
- 32. Расчётная таблица
- 33. Слайд 33
- 34. Слайд 34
- 35. Скачать презентанцию
Математическая статистика - это раздел математики, посвящённый математическим методам сбора, систематизации, обработки, анализа и использования экспериментальных данных.
Слайды и текст этой презентации
Слайд 2Математическая статистика -
это раздел математики, посвящённый математическим
методам сбора, систематизации, обработки, анализа и использования экспериментальных данных.
Слайд 4Пусть требуется изучить некоторую совокупность объектов относительно некоторого количественного или
качественного признака.
Иногда проводят сплошное обследование.
На практике чаще всего делают выборку,
т.е. отбирают часть объектов совокупности.
Слайд 6Дискретным вариационным рядом называется ранжированный в порядке возрастания ряд вариантов
с соответствующими им частотами или частостями.
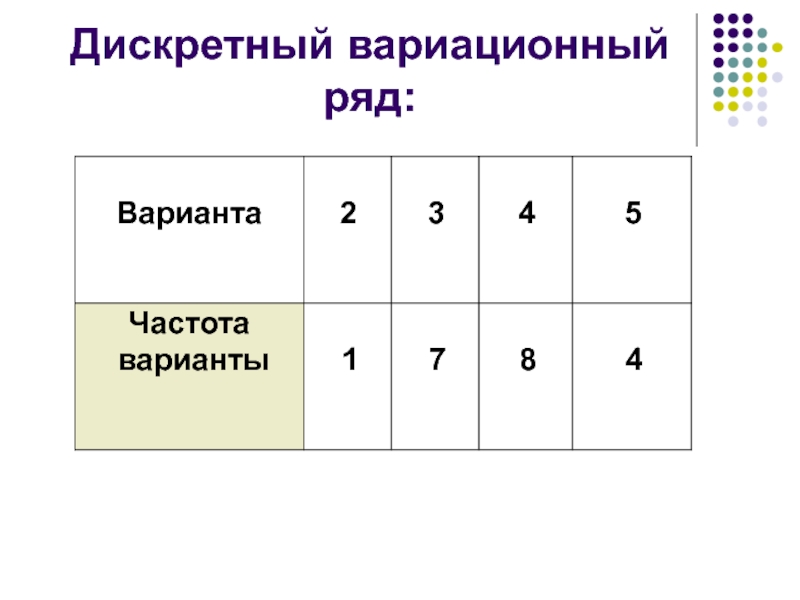
Слайд 7Пример. 20 студентов на экзамене по психологии получили такие оценки
(по пятибалльной системе): 5, 4, 4, 3, 3, 5, 2,
3, 4, 3, 3, 4, 4, 4, 3, 5, 4, 4, 3 ,5. Составить дискретный вариационный ряд.
Слайд 9Пример. Имеются данные о заработной плате сотрудников предприятия за сентябрь
2012 г., тыс. руб.:
10,11, 21,13,14,15,14,15,15,19,15,15,16,16,
16,19,16,16,19,19,19,16,19,17,17,17,18,18,18,18,18,18,18,18,19,15,19,20,21,20,21,21,20,12,23,23, 12,22, 12,21,21,21, 17,17,17
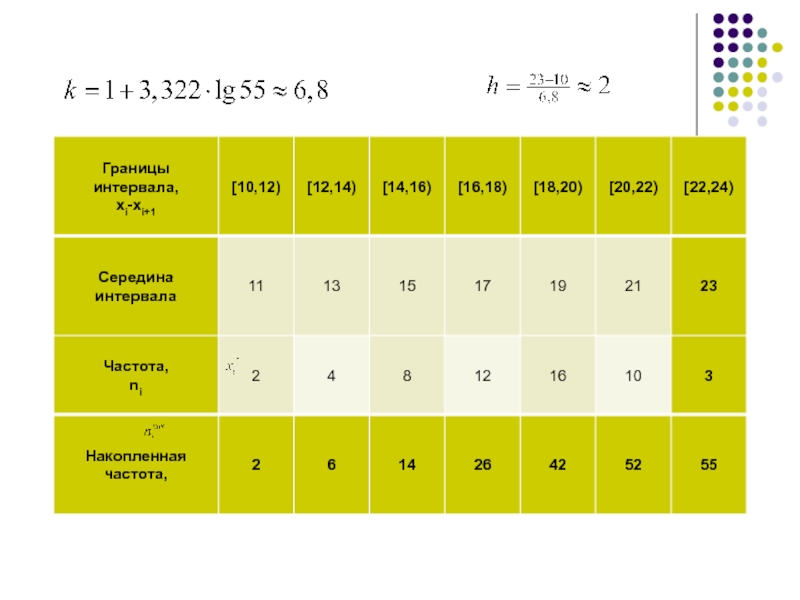
Слайд 10Если число различных значений признака в выборке велико, или признак
является непрерывным (т.е. может принять любое значение в некотором интервале),
то составляют интервальный вариационный ряд: нужно весь промежуток изменения значений выборки (от минимального до максимального) разбить на интервалы, а затем подсчитать число значений из выборки, попадающих в каждый интервал (частоты).При этом оптимальное количество интервалов определяется по формуле
а длина интервала
Слайд 14Полигоном частот (относительных частот) интервального ряда называется ломаная с вершинами
в точках (в
точках ) ( - середины интервалов).
Слайд 16 Гистограмма
Применяется для изображения только
интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников
с основаниями, равными интервалам значений признака и высотами, равными частотам (частостям) интервалов.При этом по оси абсцисс откладываются интервалы, а по оси ординат – частоты (или частости) в случае равенства интервалов, или плотности распределения частот (или частостей) в случае неравенства интервалов.
Слайд 18Кумулята
Кумулятивная кривая (кумулята) – кривая накопленных частот.
Представляет ломаную, соединяющую
точки
Для интервального вариационного ряда ломаная начинается с точки .
Слайд 21Средние величины
Средние величины характеризуют значение признака, вокруг которого концентрируются наблюдения
или, как говорят, центральную тенденцию распределения.
К ним относят:
среднюю арифметическую,
Моду,
медиану.
Слайд 22Средней арифметической вариационного ряда называется сумма произведений всех вариантов на
соответствующие частоты, деленная на сумму частот:
,
где xi - варианты дискретного ряда или середины интервалов интервального вариационного ряда;
ni - соответствующие им частоты.
Слайд 23Мода (Mo) - это значение, которое встречается в выборке
наиболее часто.
Мода может быть приближённа найдена по гистограмме: выбираем самую
высокую ступеньку, её вершины крест-накрест соединяем с вершинами предшествующей и следующей за ней степеньками, из точки пересечения опускаем перпендикуляд на ось ОХ, это и есть мода.
Слайд 26Медиана Me - это значение, которое делит вариационный ряд
пополам.
Медиана может быть приближенно найдена с помощью кумуляты как значение
признака, для которого 
Слайд 28Показатели вариации
Дисперсией вариационного ряда называется средняя арифметическая квадратов отклонений вариантов
от их средней арифметической:
Среднее квадратическое отклонение
