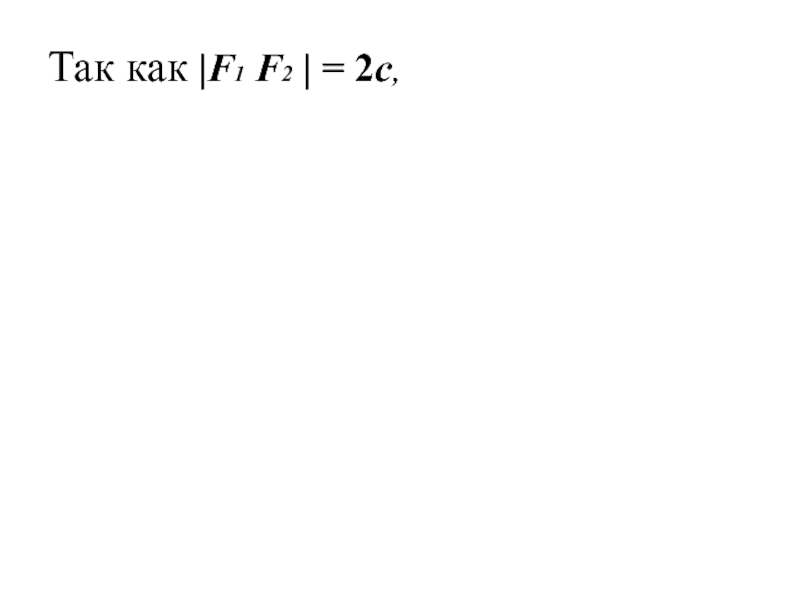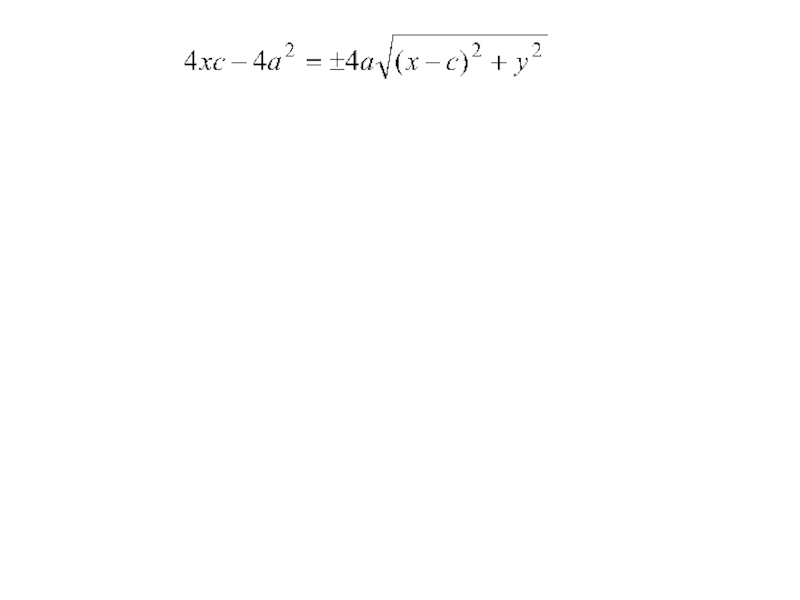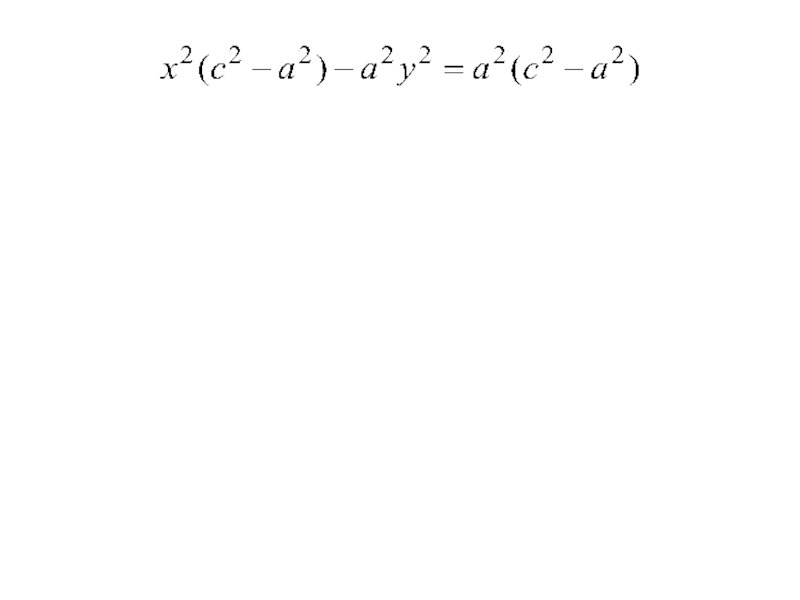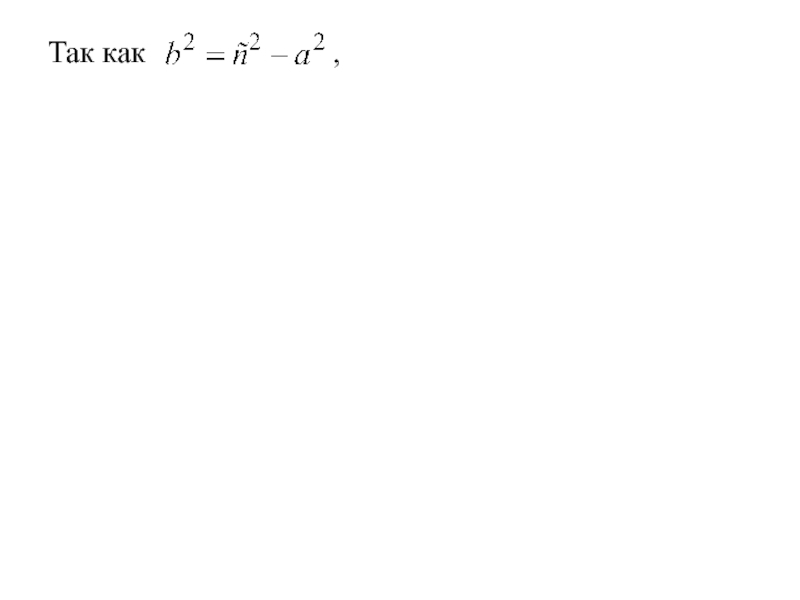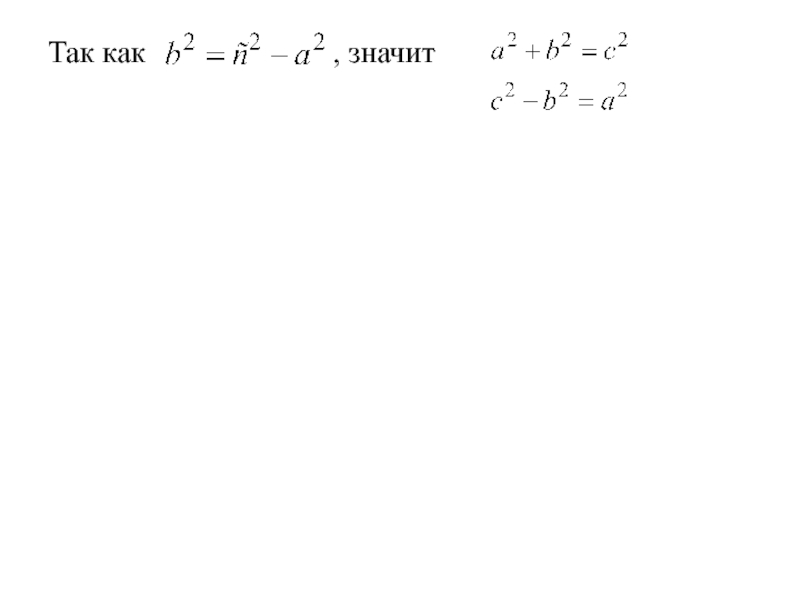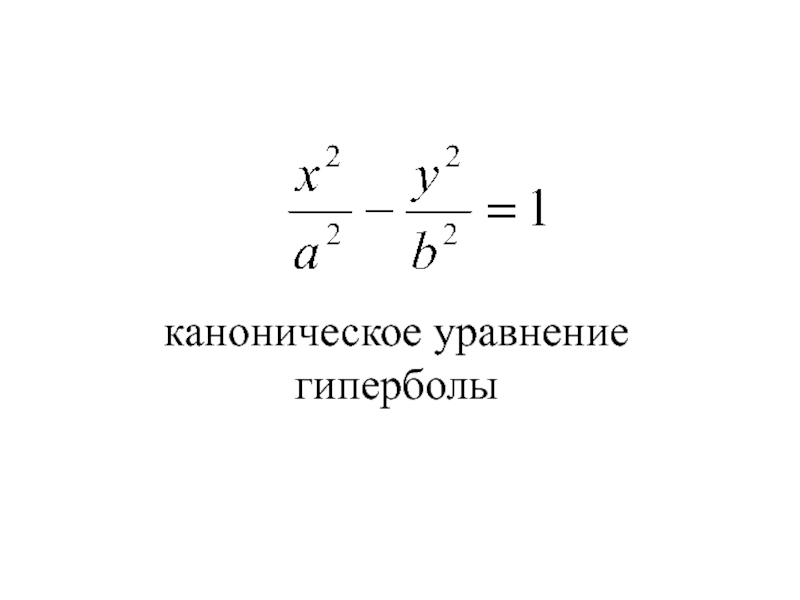Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Гипербола и её каноническое уравнение
Содержание
- 1. Гипербола и её каноническое уравнение
- 2. 4. Гипербола и её каноническое уравнение
- 3. 4. Гипербола и её каноническое уравнениеГиперболой называется
- 4. M
- 5. F1 M
- 6. F1 F2 M
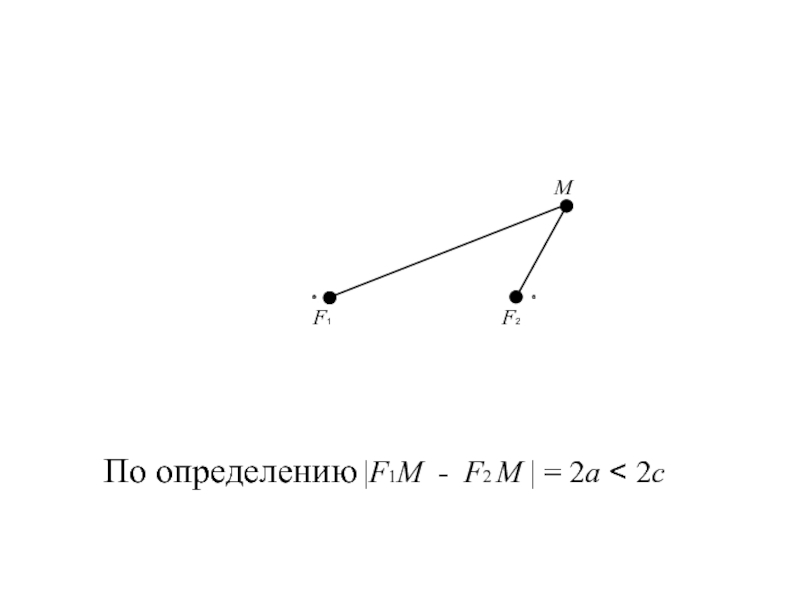
- 7. По определению |F1М - F2 М | = 2a < 2c
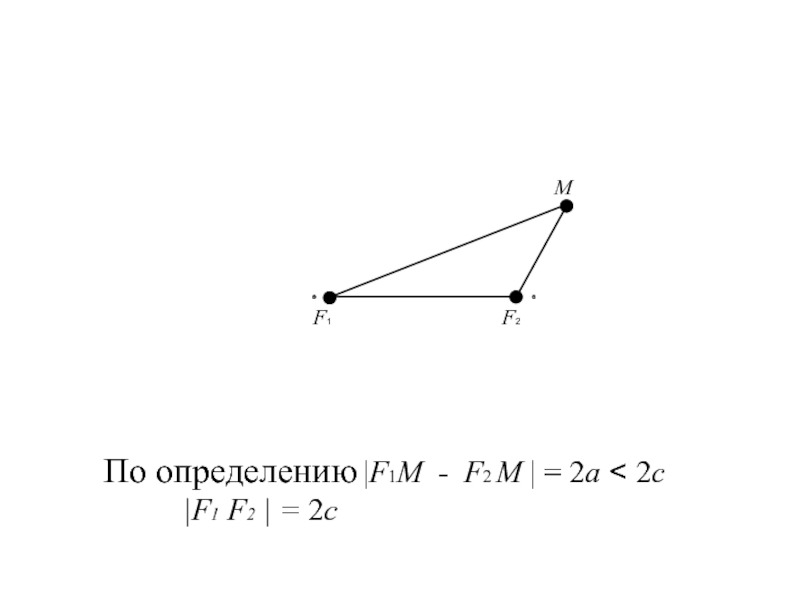
- 8. По определению |F1М - F2 М | = 2a < 2c |F1 F2 | = 2c
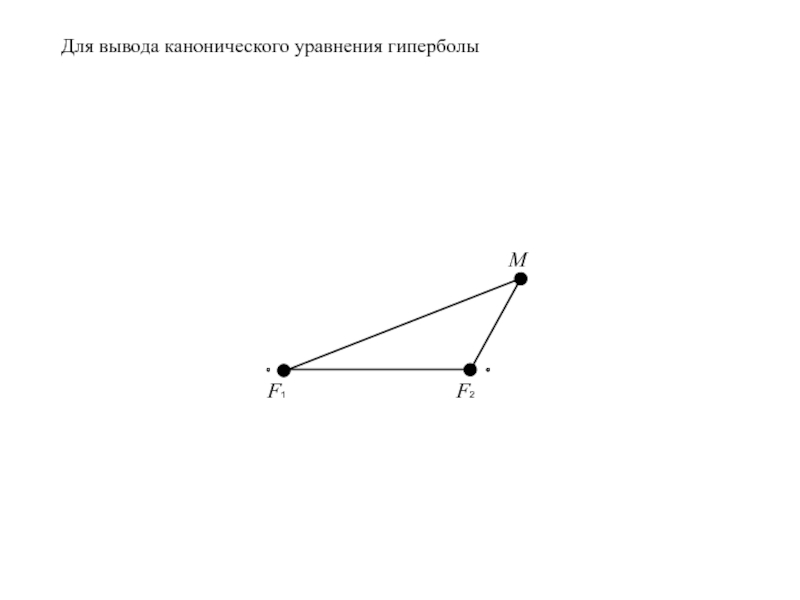
- 9. Для вывода канонического уравнения гиперболы
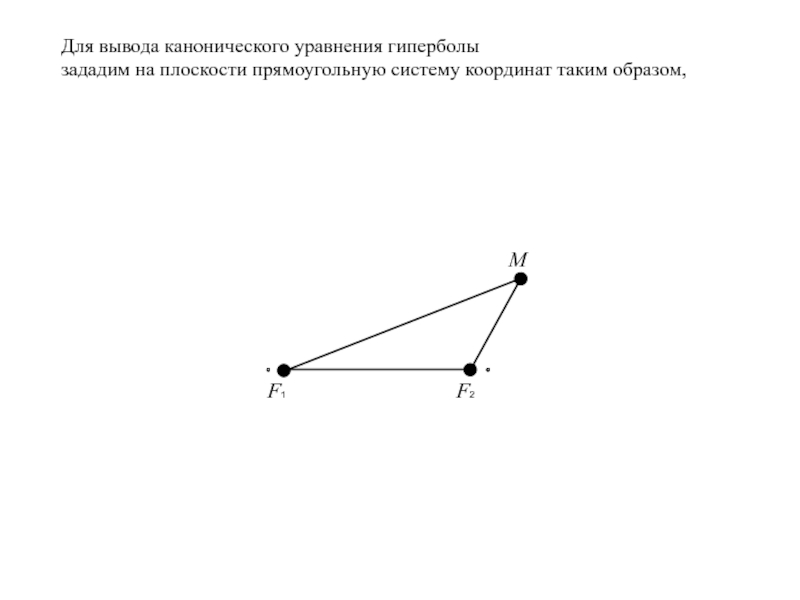
- 10. Для вывода канонического уравнения гиперболы зададим на плоскости прямоугольную систему координат таким образом,
- 11. Для вывода канонического уравнения гиперболы зададим на
- 12. Для вывода канонического уравнения гиперболызададим на плоскости
- 13. Для вывода канонического уравнения эллипса зададим на
- 14. Для вывода канонического уравнения эллипса зададим на
- 15. Для вывода канонического уравнения эллипса зададим на
- 16. Так как |F1 F2 | = 2c,
- 17. Так как |F1 F2 | = 2c,
- 18. Так как |F1 F2 | = 2c,
- 19. Так как |F1 F2 | = 2c,
- 20. Так как |F1 F2 | = 2c,
- 21. По определению |F1М - F2 М | = 2a (1)Получим
- 22. По определению |F1М - F2М | = 2a (1) Получим
- 23. По определению |F1М - F2М | =
- 24. По определению |F1М - F2М | =
- 25. По определению |F1М - F2М | =
- 26. По определению |F1М - F2М | =
- 27. По определению |F1М - F2М | =
- 28. Слайд 28
- 29. Разделим на 4 и возведём обе части в квадрат
- 30. Разделим на 4 и возведём обе части в квадрат
- 31. Разделим на 4 и возведём обе части в квадрат
- 32. Разделим на 4 и возведём обе части в квадрат
- 33. Слайд 33
- 34. Так как по определению a < c, обозначим
- 35. Так как по определению a < c, обозначим
- 36. Так как по определению a < c, обозначимполучим выражение
- 37. Так как по определению a < c,
- 38. Так как по определению a < c,
- 39. Мы доказали, что координаты любой точки гиперболы удовлетворяют уравнению (2)
- 40. Докажем обратное: если координаты некоторой точки М(x,y)
- 41. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 42. Пусть точка M (x; y) удовлетворяет уравнению (2), тогда выразим :подставим
- 43. Так как ,
- 44. Так как , значит
- 45. Так как
- 46. Так как
- 47. Так как
- 48. Так как
- 49. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 50. Отрезки F1M и F2M назовем фокальными радиусами гиперболы
- 51. Отрезки F1M и F2M назовем фокальными радиусами
- 52. Отрезки F1M и F2M назовем фокальными радиусами
- 53. Отрезки F1M и F2M назовем фокальными радиусами
- 54. Отрезки F1M и F2M назовем фокальными радиусами
- 55. Отрезки F1M и F2M назовем фокальными радиусами
- 56. Отрезки F1M и F2M назовем фокальными радиусами
- 57. Отрезки F1M и F2M назовем фокальными радиусами
- 58. Таким образом, получаем если
- 59. Таким образом, получаем если
- 60. Таким образом, получаем если
- 61. Таким образом, получаем если
- 62. Таким образом, получаем если
- 63. Таким образом, получаем если
- 64. Таким образом, получаем если
- 65. Таким образом, получаем если
- 66. Таким образом, уравнение (2) есть уравнение гиперболы,
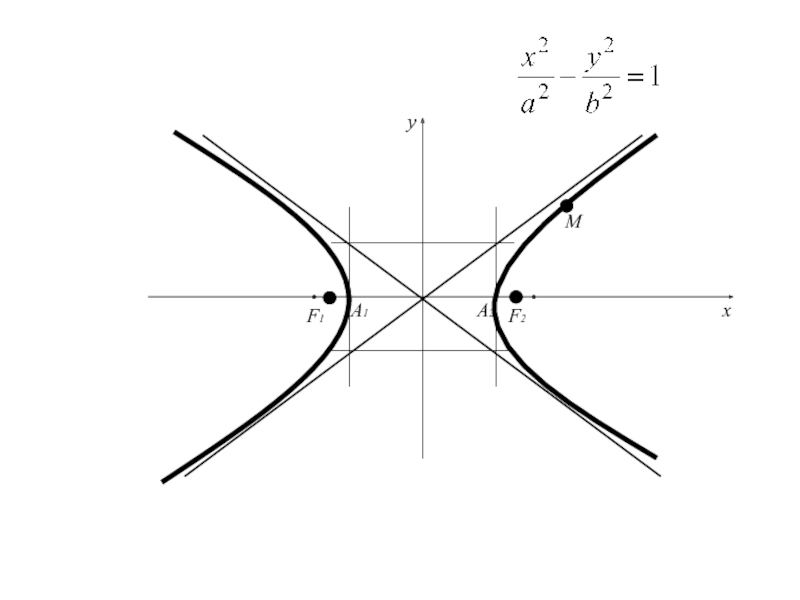
- 67. каноническое уравнение гиперболы
- 68. 5. Исследование формы гиперболы
- 69. 5. Исследование формы гиперболыТ.к. в каноническое уравнение гиперболы координаты x и y входят во второй степени
- 70. 5. Исследование формы гиперболыТ.к. в каноническое уравнение
- 71. 5. Исследование формы гиперболы
- 72. 5. Исследование формы гиперболы
- 73. 5. Исследование формы гиперболы
- 74. 5. Исследование формы гиперболы
- 75. 5. Исследование формы гиперболы
- 76. 5. Исследование формы гиперболы
- 77. 5. Исследование формы гиперболы
- 78. 5. Исследование формы гиперболы
- 79. 5. Исследование формы гиперболы
- 80. 5. Исследование формы гиперболы
- 81. 5. Исследование формы гиперболы
- 82. 5. Исследование формы гиперболы
- 83. 5. Исследование формы гиперболы
- 84. 5. Исследование формы гиперболы
- 85. xy
- 86. xy
- 87. xyM
- 88. xyMd
- 89. xyMd
- 90. В силу того, что гипербола, заданная каноническим
- 91. Так как гипербола, заданная каноническим уравнением, симметрична
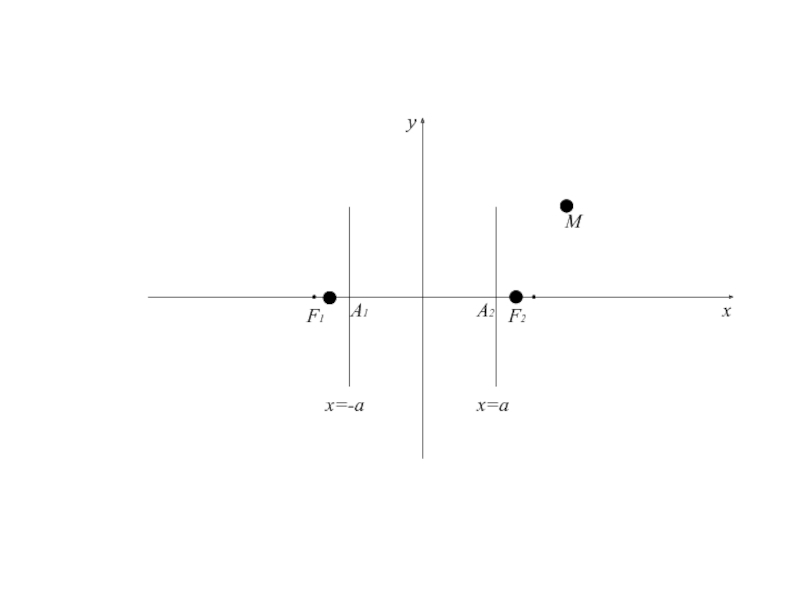
- 92. x=-aA1A2F1F2Mxyx=a
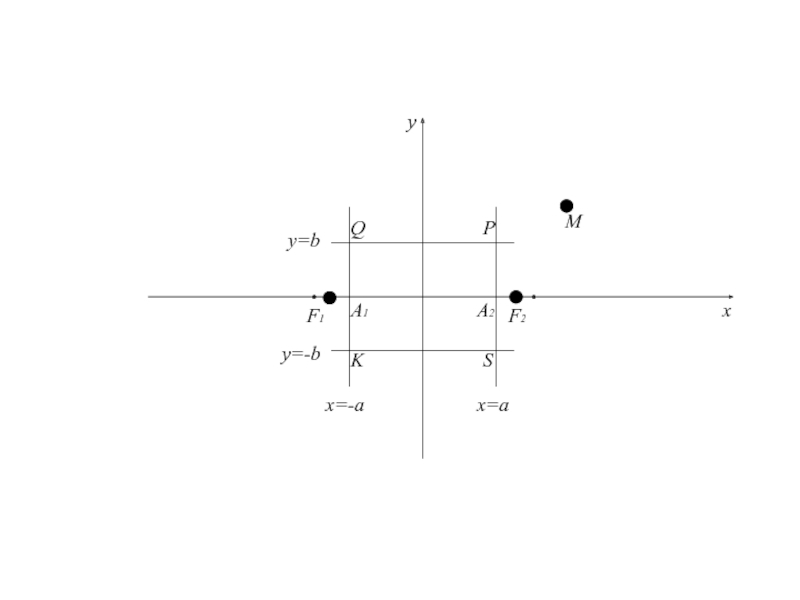
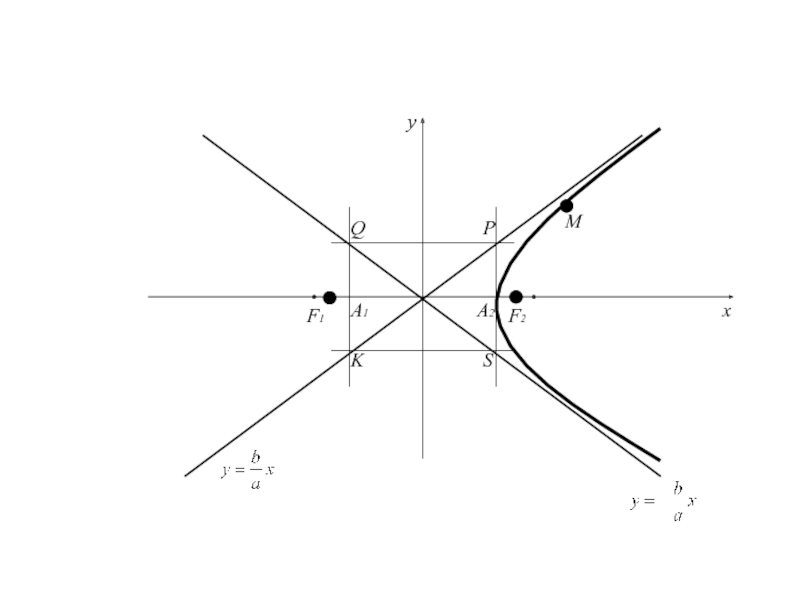
- 93. PQSKA1A2F1F2Mxyx=-ax=ay=-by=b
- 94. PQSKA1A2F1F2Mxy
- 95. PQSKA1A2F1F2Mxy
- 96. PQSKA1A2F1F2Mxy
- 97. PQSKA1A2F1F2Mxy
- 98. A1A2F1F2Mxy
- 99. Гипербола, у которой полуоси равны, называется равностороннейУравнения её асимптот
- 100. 6. Эксцентриситет и директрисы гиперболы
- 101. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 102. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 103. 6. Эксцентриситет и директрисы гиперболы Отношение расстояния
- 104. Перепишем формулы для фокальных радиусов если
- 105. Перепишем формулы для фокальных радиусов если
- 106. Две прямые, перпендикулярные действительной оси гиперболы и
- 107. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют вид
- 108. Для гиперболы, заданной каноническим уравнениемуравнения директрис имеют
- 109. A1A2F1F2Mxy
- 110. A1A2F1F2Mxy
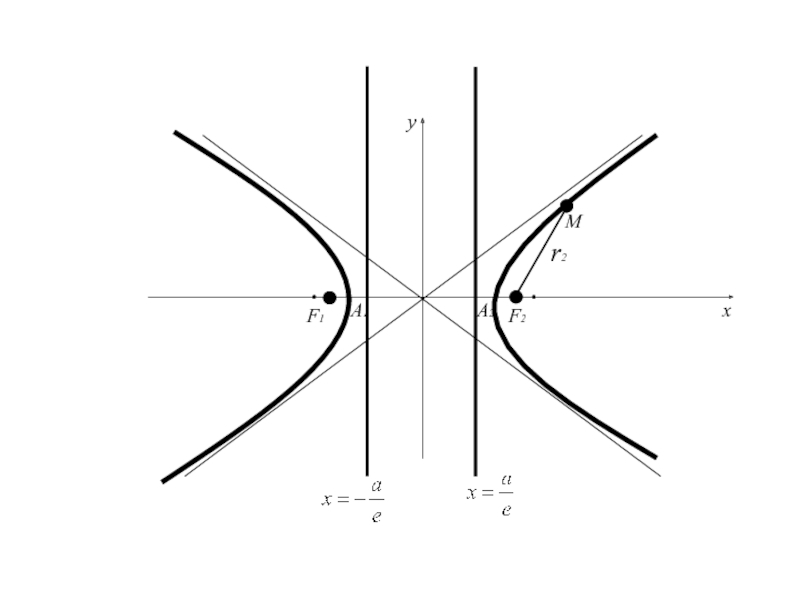
- 111. Теорема: Для того чтобы точка лежала на
- 112. A1A2F1F2Mxyr2
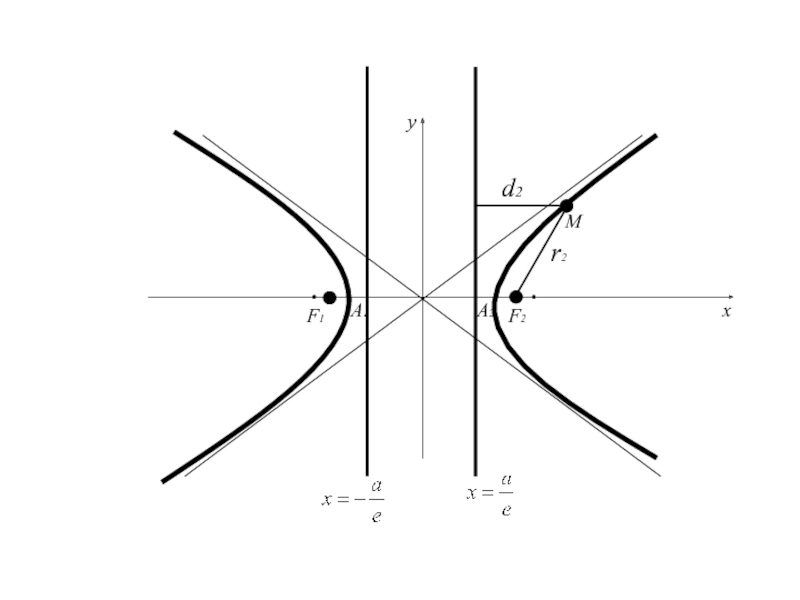
- 113. A1A2F1F2Mxyr2d2
- 114. A1A2F1F2Mxyr2d2
- 115. Самостоятельно изучить вопросы по данной теме:Понятие сопряженной гиперболыУравнение касательной к гиперболеОптическое свойство гиперболы
- 116. Скачать презентанцию
Слайды и текст этой презентации
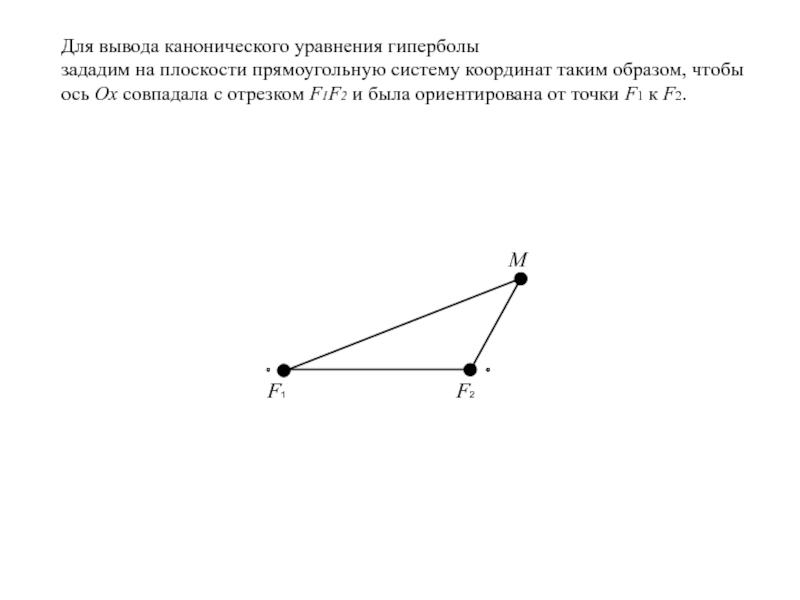
Слайд 10Для вывода канонического уравнения гиперболы
зададим на плоскости прямоугольную систему
координат таким образом,
Слайд 11Для вывода канонического уравнения гиперболы
зададим на плоскости прямоугольную систему
координат таким образом, чтобы ось Ox совпадала с отрезком F1F2
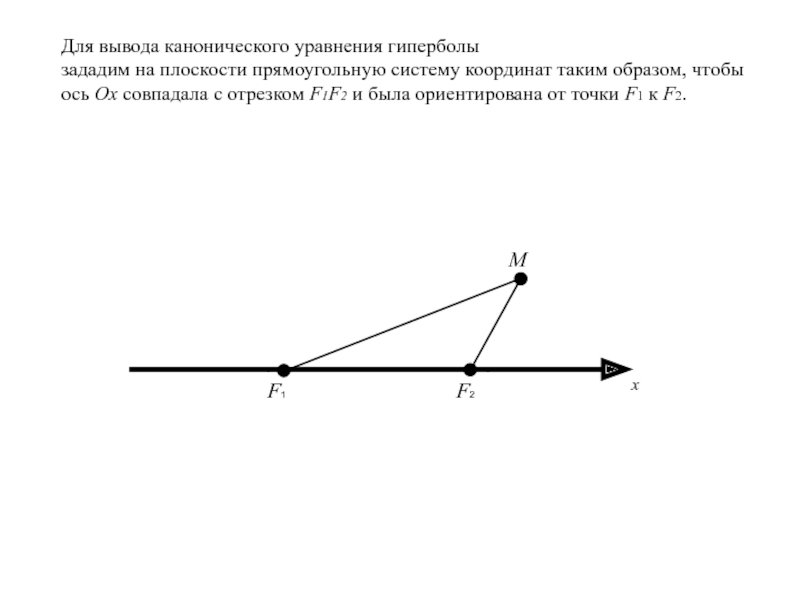
и была ориентирована от точки F1 к F2.Слайд 12Для вывода канонического уравнения гиперболы
зададим на плоскости прямоугольную систему координат
таким образом, чтобы ось Ox совпадала с отрезком F1F2 и
была ориентирована от точки F1 к F2.x
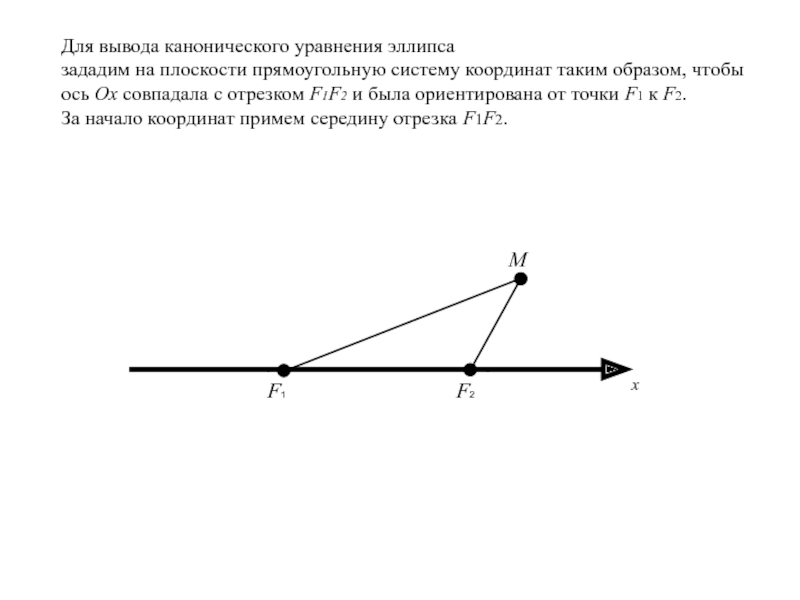
Слайд 13Для вывода канонического уравнения эллипса
зададим на плоскости прямоугольную систему
координат таким образом, чтобы ось Ox совпадала с отрезком F1F2
и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
x
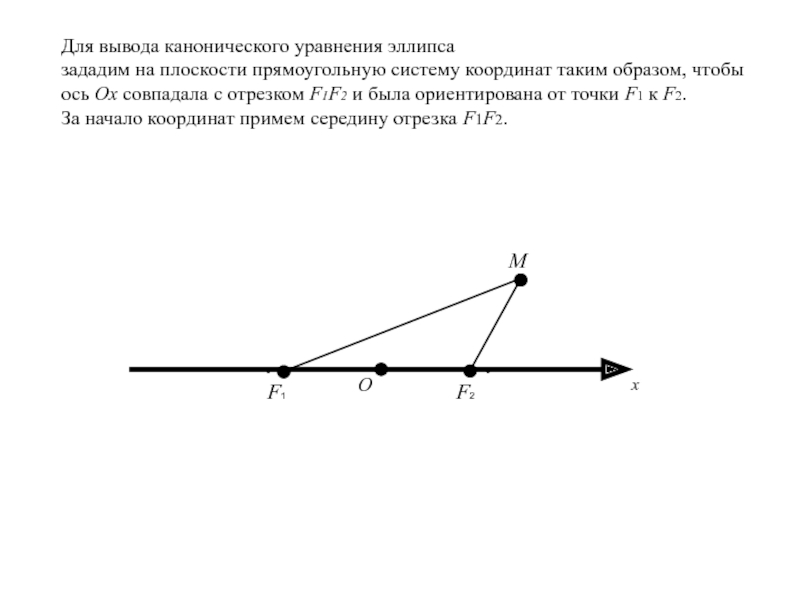
Слайд 14Для вывода канонического уравнения эллипса
зададим на плоскости прямоугольную систему
координат таким образом, чтобы ось Ox совпадала с отрезком F1F2
и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
x
F1
F2
M
О
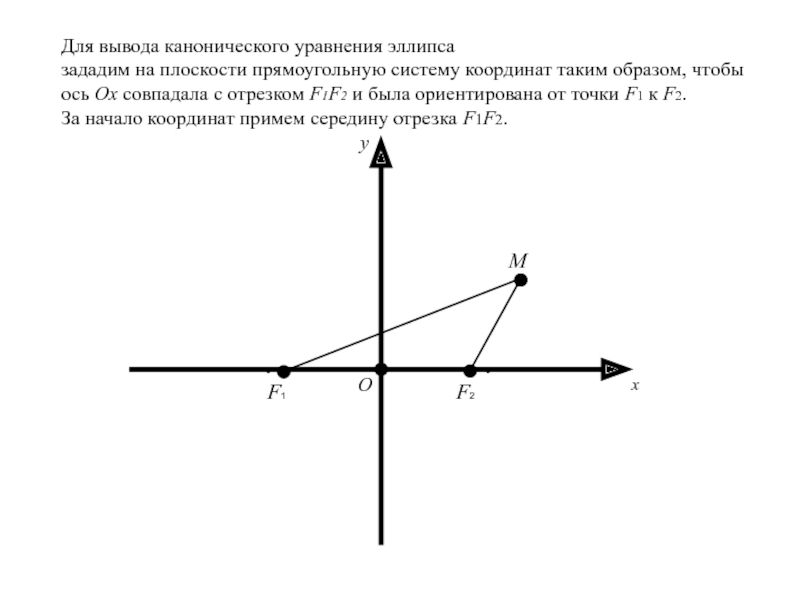
Слайд 15Для вывода канонического уравнения эллипса
зададим на плоскости прямоугольную систему
координат таким образом, чтобы ось Ox совпадала с отрезком F1F2
и была ориентирована от точки F1 к F2.За начало координат примем середину отрезка F1F2.
x
F1
F2
M
О
y
Слайд 18Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
Слайд 19Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогдаСлайд 20Так как |F1 F2 | = 2c,
значит в выбранной
системе координат фокусы имеют координаты
F1 (-c; 0), F2
(с; 0)
произвольная точка M(x,y),
тогда
Слайд 25По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 26По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 27По определению |F1М - F2М | = 2a (1)
Получим
избавимся
от модуля и преобразуем
возведём обе части в квадрат
Слайд 40
Докажем обратное: если координаты некоторой точки М(x,y) удовлетворяют уравнению (2),
то для этой точки выполнятся равенство |F1М - F2 М
| = 2a (1)
Слайд 53Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 54Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Слайд 55Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если
Слайд 56Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или
Слайд 57Отрезки F1M и F2M назовем фокальными радиусами гиперболы
Из уравнения
следует, что
Если , то в силу соотношения
будем иметь
Если или , то
Слайд 64Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 65Таким образом, получаем
если
если
Подставим в равенство
(|F1М - F2 М | = 2a)
если выполняется
если , то
Слайд 66Таким образом, уравнение (2) есть уравнение гиперболы, т.к. доказано, что
координаты любой точки M (x; y) гиперболы, т.е. любой точки,
для которой выполняется выражение (1) удовлетворяет уравнению (2) и обратно, если два числа x и y удовлетворяет уравнению (2), то точка M (x; y) удовлетворяет соотношению (1), т.е. лежит на гиперболе.Слайд 69 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени
Слайд 70 5. Исследование формы гиперболы
Т.к. в каноническое уравнение гиперболы координаты x
и y входят во второй степени => оси Ox и
Oy являются осями симметрии гиперболы, а начало координат центром симметрии.Слайд 71 5. Исследование формы гиперболы
Из уравнения => что
,т.е. и Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Слайд 72 5. Исследование формы гиперболы
Из уравнения => что
,т.е. и Геометрически это означает, что между прямыми x=a и x=-a нет точек гиперболы.
Ось симметрии Oy не пересекает гиперболу и называется мнимой осью.
Слайд 73 5. Исследование формы гиперболы
Ось симметрии Ox пересекает гиперболу
в двух точках A1(-a;0) A2(a;0) – вершины гиперболы и называется действительной осью.Слайд 74 5. Исследование формы гиперболы
Ось симметрии Ox пересекает гиперболу
в двух точках A1(-a;0) A2(a;0) – вершины гиперболы и называется действительной осью.a и b в уравнении гиперболы называются соответственно действительной и мнимой полуосями гиперболы.
Слайд 75 5. Исследование формы гиперболы
Выразим y из уравнения гиперболы
и возьмем положительное значение
Слайд 76 5. Исследование формы гиперболы
Выразим y из уравнения гиперболы
и возьмем положительное значение считая, что получим точки гиперболы, лежащие в I четверти.
Слайд 77 5. Исследование формы гиперболы
Выразим y из уравнения гиперболы
и возьмем положительное значение считая, что получим точки гиперболы, лежащие в I четверти.
Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 78 5. Исследование формы гиперболы
Выразим y из уравнения гиперболы
и возьмем положительное значение считая, что получим точки гиперболы, лежащие в I четверти.
Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 79 5. Исследование формы гиперболы
Выразим y из уравнения гиперболы
и возьмем положительное значение считая, что получим точки гиперболы, лежащие в I четверти.
Из уравнения (3) => что y в полуинтервале есть возрастающая функция при этом предел
Слайд 80 5. Исследование формы гиперболы
Всякая прямая пересекает гиперболу не
более чем в двух точках, так как прямая определяется уравнением I степени, а гипербола - II
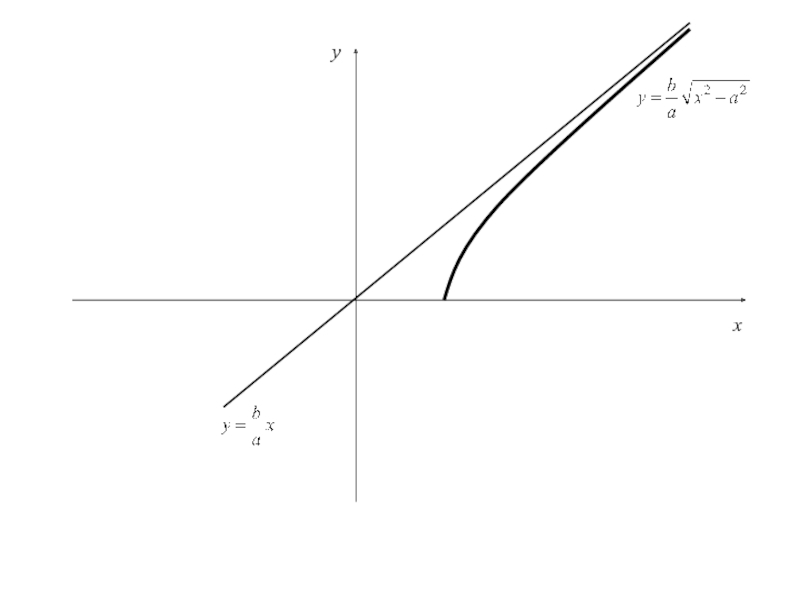
Слайд 81 5. Исследование формы гиперболы
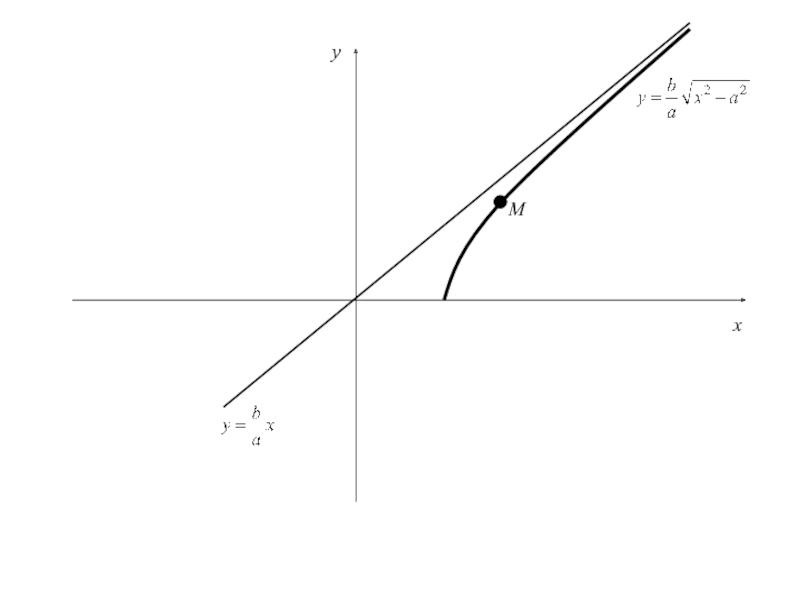
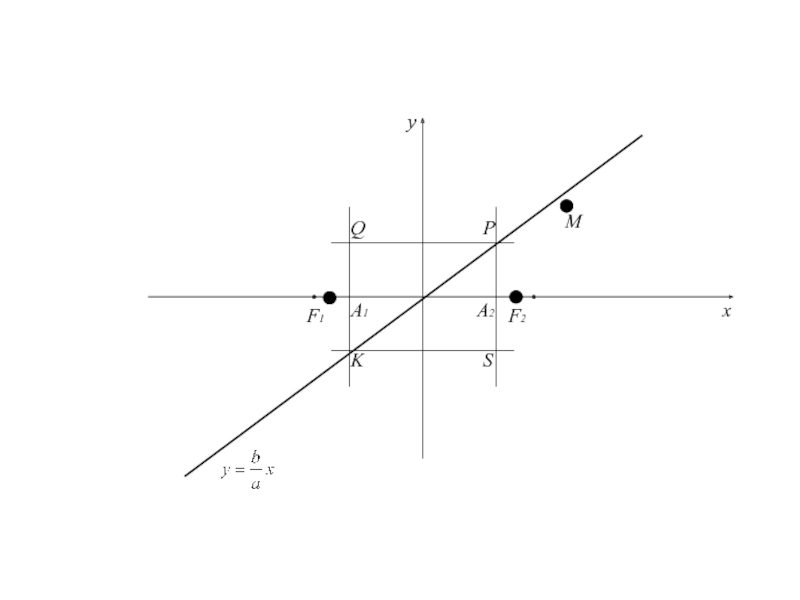
Рассмотрим уравнение прямой
или Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):
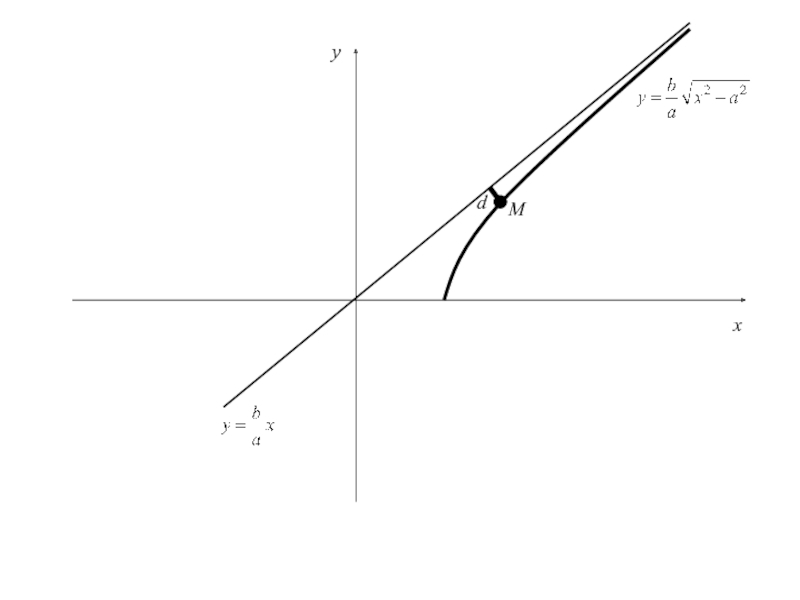
Слайд 82 5. Исследование формы гиперболы
Рассмотрим уравнение прямой
или Найдем расстояние d от точки M(x,y), лежащей на дуге гиперболы, определенной уравнением (3), до прямой (4):
Слайд 83 5. Исследование формы гиперболы
Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
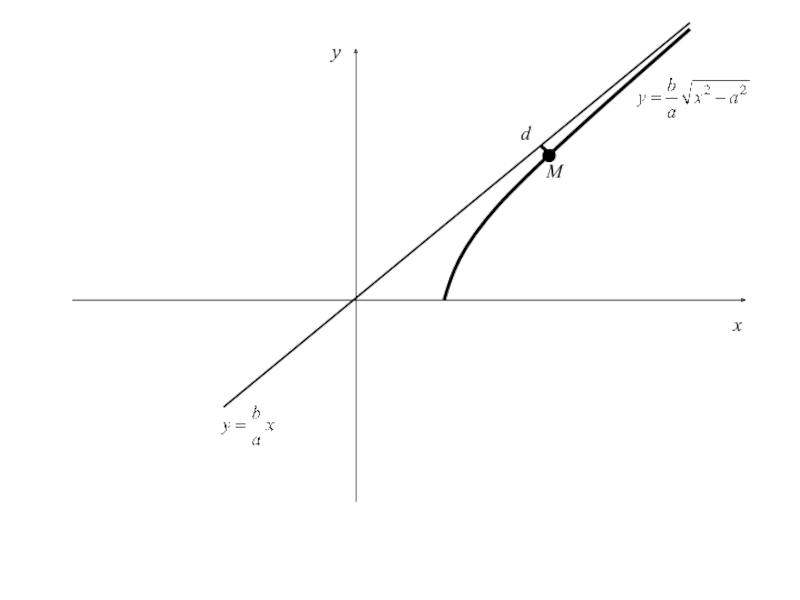
Слайд 84 5. Исследование формы гиперболы
Получили, что на полуинтервале
расстояние d от точки M(x,y) рассматриваемой части гиперболы до прямой (4) есть убывающая функция и(т.е. расстояние стремиться к 0)
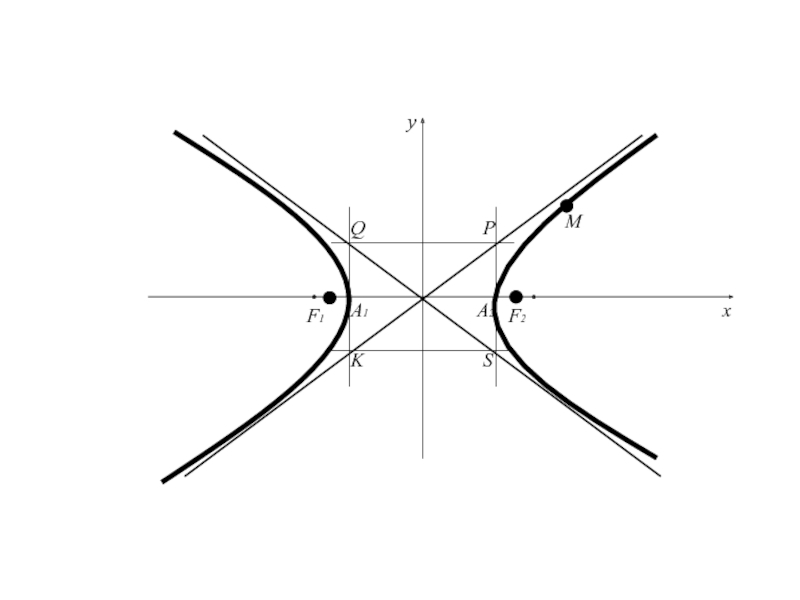
Прямая, определяемая уравнением называется асимптотой гиперболы.
Слайд 90В силу того, что гипербола, заданная каноническим уравнением, симметрична относительно
начала координат, расстояние от точки М(x;y), лежащей на дуге гиперболы,
заданой
уравнением до прямой
стремится к нулю при
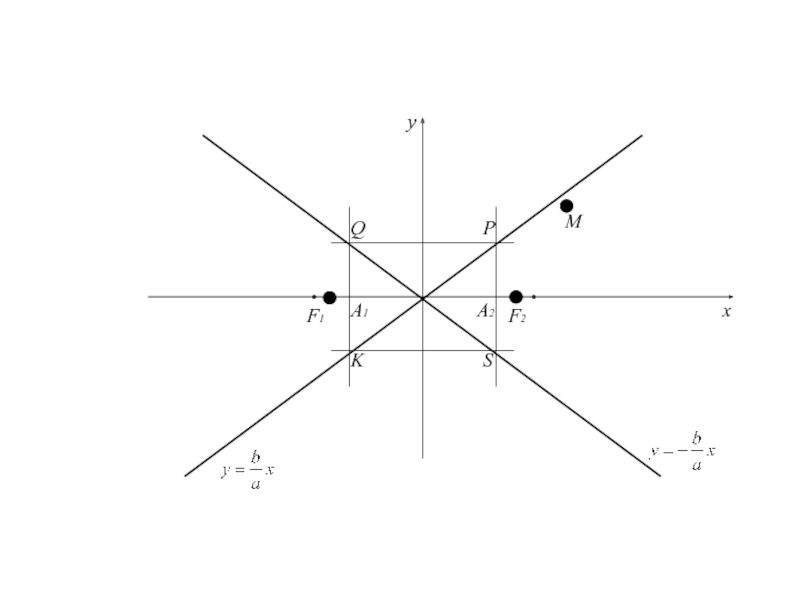
Слайд 91Так как гипербола, заданная каноническим уравнением, симметрична относительно оси Оy,
то она имеет вторую асимптоту
которая обладает свойством аналогичным свойству первой
асимптоты по отношению к дугам гиперболы, расположенной в II и IV четвертях .Асимптоты являются диагоналями прямоугольника с вершинами Р(а;b), Q(-a;b), S(a;-b), K(-a;-b).
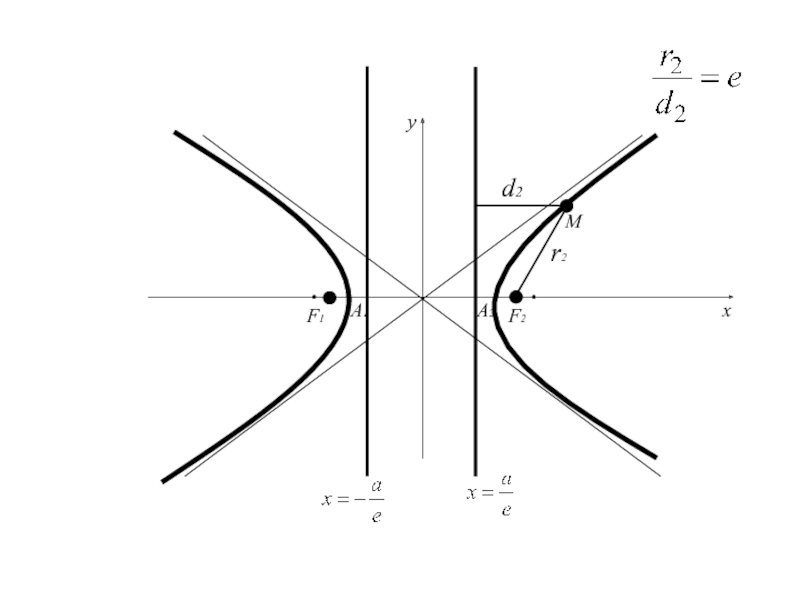
Слайд 1016. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еСлайд 1026. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой е
Слайд 1036. Эксцентриситет и директрисы гиперболы
Отношение расстояния от центра гиперболы
до фокуса к действительной полуоси гиперболы называется эксцентриситетом гиперболы и
обозначается буквой еТак как для гиперболы 0 < а < с, то е >1
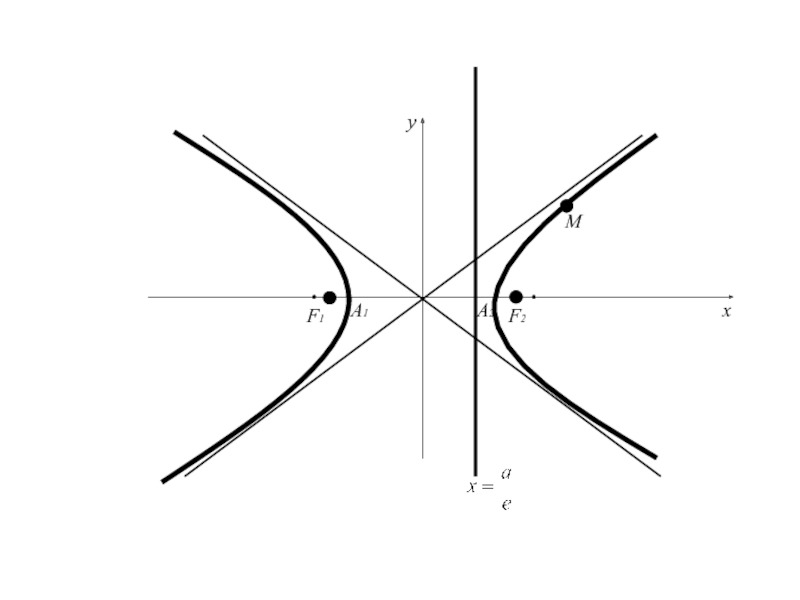
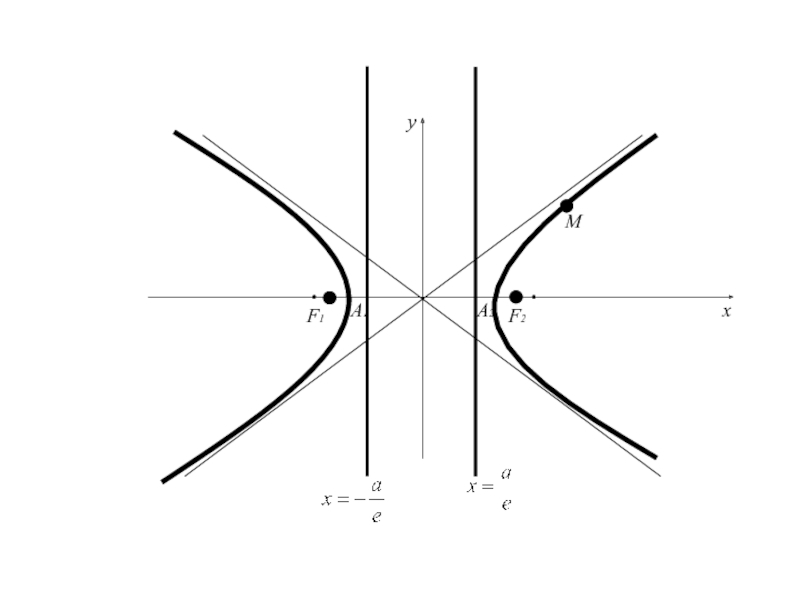
Слайд 106Две прямые, перпендикулярные действительной оси гиперболы и отстоящие от центра
гиперболы на расстояние а/е (где a – действительная полуось, е
– эксцентриситет гиперболы), называются директрисами гиперболыСлайд 108Для гиперболы, заданной каноническим уравнением
уравнения директрис имеют вид
Т.к. e
>1, то директрисы отстоят от центра на расстоянии меньшем действительной
полуоси.