Преобразования на плоскости

векторы.

2. Уравнения прямой и плоскости.

3. Аналитическое представление кривых и

поверхностей.

4. Пересечение луча с плоскостью и сферой.

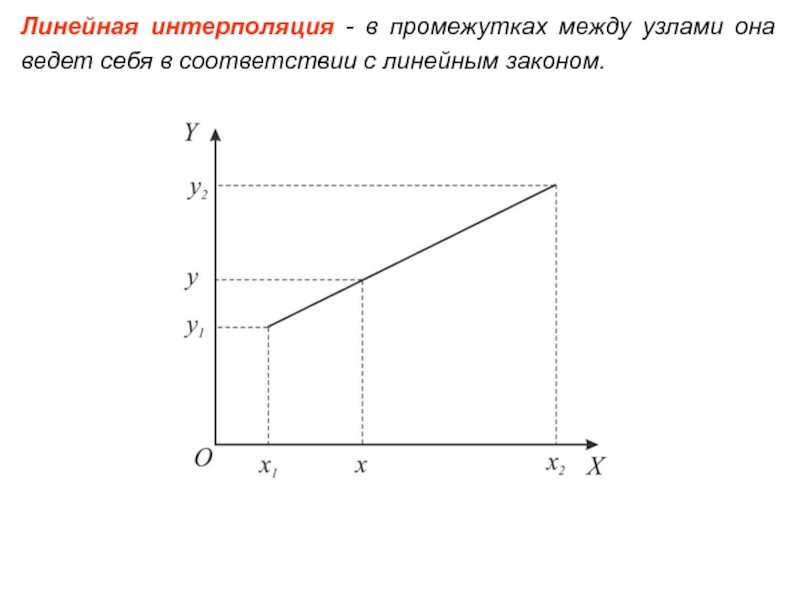
. 5. Интерполяция функций одной и двух переменных.

точками?
и
Что такое вектор?
Какие вектора называются коллиниарными?
-

Что является суммой двух векторов?

- Что является линейной комбинацией векторов?

- Какие вектора называются компланарными?

зависимыми?
- Что является скалярным произведением двух векторов?
- Что является векторным

произведением двух векторов?

системе координат можно задать уравнением вида

для
случая, когда прямая не параллельна оси OY, и уравнением
для вертикальной прямой.

Задать прямую можно с использованием вектора направления этой прямой и точки, лежащей на этой прямой

Параметрическое уравнение прямой:

в котором параметр t пробегает все значения числовой прямой.

в пространстве задается аналогично:
Через каждую точку плоскости можно провести единственную

прямую, перпендикулярную данной плоскости. Все эти прямые будут параллельны друг другу, значит, они имеют общий вектор направления. Этот вектор - нормаль к плоскости. Если длина вектора равна единице, это единичная нормаль.

и какую-либо точку, принадлежащую данной плоскости.
- вектор единичной

нормали,
- некоторая точка на плоскости.

Тогда для любой точки лежащей на плоскости, вектор будет ортогонален вектору нормали, а следовательно, выполняется равенство

Каноническое уравнение плоскости:

множитель, то оно будет описывать ту же самую плоскость, но

если вектор имеет единичную длину, то задает расстояние от начала координат до данной плоскости.

Пусть три точки , не лежащие на одной прямой, имеют координаты:

Для получения канонического уравнения необходимо построить нормаль к плоскости, используем для этого операцию векторного произведения.

вид:
Определим значение . Так как точка

принадлежит этой плоскости, то ее координаты должны удовлетворять полученному уравнению. Подставим их в уравнение и получим:

это геометрическое место точек удовлетворяющих уравнению

где - функция двух переменных.

Задают ли следующие уравнения линии?

значениями на некотором дискретном множестве точек (узлов) из области определения

и необходимо получить значение функции в какой-либо точке, не совпадающей с узлом, используют различные методы приближенного вычисления, которые основываются на некоторых априорных предположениях относительно этой функции.

Интерполяция – точка, в которой ищется значение функции, принадлежит заданной области.

Экстраполяция – точка лежит вне области.

в соответствии с линейным законом.

с помощью кусочно-линейной функции).

этой системы уравнений:

интерполяции кривых и поверхностей используются сплайн-функции, которые гладко "склеиваются" из

полиномов. Среди них следует выделить кубические сплайны, которые строятся из полиномов третьей степени. Они широко используются в инженерной геометрии благодаря простоте их вычисления и другим полезным свойствам.