Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы оптимизации
Содержание
- 1. Численные методы оптимизации
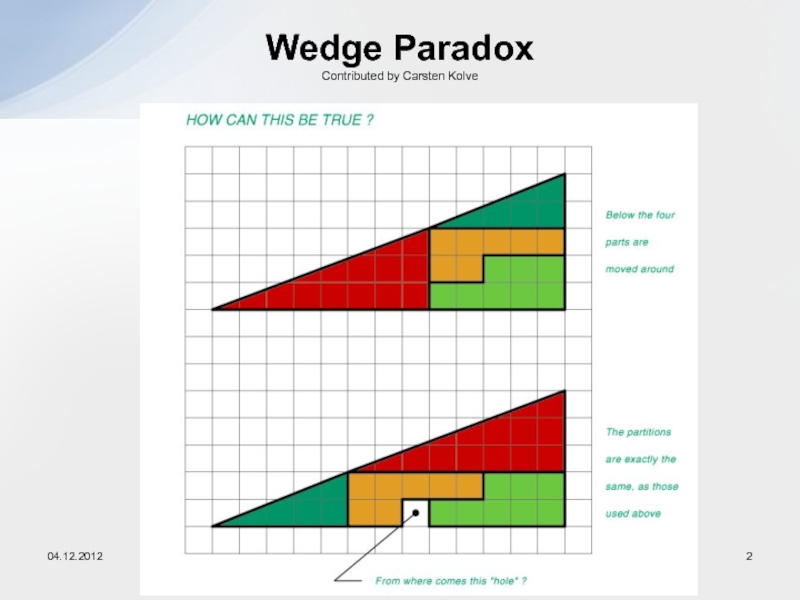
- 2. Wedge Paradox Contributed by Carsten Kolve04.12.2012
- 3. 04.12.2012Нанооптика Проектирование тонкопленочных структур используется в
- 4. 04.12.2012Проектирование оптических покрытий состоит из следующих этапов
- 5. 04.12.2012Методы оптимизацииМетоды условной оптимизацииМетоды безусловной оптимизации
- 6. Что такое оптимизация?Задача оптимизации: Максимизация или минимизация
- 7. Что такое оптимизация?Цель изучения: Усвоение практических и
- 8. Свойства оптимизации как математической дисциплиныОписательная – предписывающая
- 9. Свойства оптимизации как математической дисциплиныЛинейные/нелинейные – выпуклые/невыпуклые:
- 10. Свойства оптимизации как математической дисциплиныКонечномерная оптимизация: Случай,
- 11. Конечномерная оптимизацияОграничения типа равенств и неравенств: Это
- 12. Конечномерная оптимизацияЛинейные ограничения : Это условия вида
- 13. Конечномерная оптимизацияПараметры (данные) : Следует различать искомые
- 14. Математическое программированиеМатематическое программирование – синоним конечномерной минимизации.
- 15. - площадь поверхности коробки с банками.Пример №1.
- 16. Пример №1. Дизайн коробки.Общее ограничение. Сторона ящика
- 17. Пример №1. Дизайн коробки.Резюме. Искомыми переменными являются
- 18. Пример №1. Дизайн коробки.Напомним, требуется определить радиус
- 19. Пример №1. Подробное рассмотрениеИзбыточные ограничения. Очевидно, что
- 20. Пример №1. Подробное рассмотрениеИзбыточные переменные. Конечно же,
- 21. Пример №1. Подробное рассмотрениеВыпуклость. Даже с учетом
- 22. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
Константин Ловецкий
Декабрь 2012
Кафедра систем телекоммуникаций
Применение методов оптимизации
04.12.2012
Слайд 304.12.2012
Нанооптика
Проектирование тонкопленочных структур используется в производстве:
жидкокристаллических дисплеев
солнечных батарей на основе
диэлектриков
Слайд 404.12.2012
Проектирование оптических покрытий состоит из следующих этапов
Физическая модель
Математическая модель
Целевая функция – мера качества модели
Решение оптимизационной
задачиСлайд 6Что такое оптимизация?
Задача оптимизации: Максимизация или минимизация
некоторой функции на
некотором множестве, часто представляющем собой множество выборов в определенной ситуации.
Функционально существует возможность сравнения различных выборов для определения «наилучшего».Области применения: Минимальная стоимость, максимальный доход, оптимальное управление, вариационное исчисление, создание новых конструкций и приборов.
04.12.2012
Слайд 7Что такое оптимизация?
Цель изучения: Усвоение практических и теоретических аспектов:
Результат моделирования:
На какой результат надеяться при постановке оптимизационной задачи? Какие свойства
благоприятны, а какие нет? Что может способствовать правильной постановке задачи? К какому классу лучше отнести конкретную задачу?Анализ решения: Что подразумевается под «решением»?
Условия существования и единственности решения. Каким образом распознать и охарактеризовать решение? Что произойдет при возмущении исходной задачи?
Численные методы: Итеративные схемы решения. Существуют ли способы (локального) упрощения проблемы? Сравнение различных способов оптимизации.
04.12.2012
Слайд 8Свойства оптимизации как математической дисциплины
Описательная – предписывающая (конструктивная) математика: Большая
часть математических задач описывала ранее поведение различных (физических) систем. Появление
компьютеров позволяет использовать математику для проектирования систем с предсказуемым поведением, что обеспечивается оптимизацией.Равенства - неравенства: Оптимизация обычно имеет дело с переменными, которые лежат в определенном диапазоне, диктуемом ограничениями на допустимый результат. Это приводит к тому, что ограничения-неравенства используются гораздо чаще, чем равенства.
04.12.2012
Слайд 9Свойства оптимизации как математической дисциплины
Линейные/нелинейные – выпуклые/невыпуклые: Подразделение между линейностью
и нелинейностью задач гораздо менее важно при оптимизации, чем различие
между выпуклостью и не выпуклостью целевых функций и ограничений. Этот факт требует от математической постановки задачи совершенно новых подходов.Дифференцируемость - не дифференцируемость : Преобладание неравенств вместе с такими специальными функциями как «max» и «min» приводит к тому, что методология классической математики с опорой на гладкость поверхностей и дифференцируемость функций не является преобладающей.
04.12.2012
Слайд 10Свойства оптимизации как математической дисциплины
Конечномерная оптимизация: Случай, когда результат расчета
целевой функции соответствует выбору конечного числа действительных переменных, называемых искомыми
переменными. Обычно их обозначают черези возможный набор переменных соответствует точке
которая называется допустимой точкой.
Ограничения: Условия, налагаемые на искомые переменные, определяют множество допустимых точек в пространстве переменных задачи.
04.12.2012
Слайд 11Конечномерная оптимизация
Ограничения типа равенств и неравенств: Это условия вида (строгих
неравенств стараются избегать)
Интервальные ограничения: Условия, налагаемые на некоторые искомые переменные,
ограничивающие их изменения рамками заданных интервалов. Весьма важны в приложениях. Например, требование положительности некоторых переменных, или их ограниченность максимальными значениями.для функций
и констант
04.12.2012
Слайд 12Конечномерная оптимизация
Линейные ограничения : Это условия вида (строгих неравенств стараются
избегать)
Параметры (данные) : Задача обычно включает не только искомые переменные,
но и коэффициенты целевой функции задачи и константы ограничений. Условия, налагаемые на эти параметры , такие как их положительность, не сказываются на формулировке исходной задачи, однако они могут серьезно влиять на алгоритмы и методы решения. Именно поэтому на эти условия необходимо обращать пристальное внимание.для линейных функций
и констант
04.12.2012
Слайд 13Конечномерная оптимизация
Параметры (данные) :
Следует различать искомые переменные и коэффициенты
целевой функции задачи и константы ограничений поскольку это позволяет не
путать их при обращении к подпрограммам минимизации.Обычно все переменные и константы передаются в стандартные подпрограммы минимизации единым массивом – вектором X.
Поэтому желательно учитывать такую возможность при программировании.
04.12.2012
Слайд 14Математическое программирование
Математическое программирование – синоним конечномерной минимизации. Этот термин предшествовал
термину «компьютерное программирование», который возник на ранних стадиях развития компьютеров
при решении оптимизационных задач.Термин «программирование» в смысле «оптимизация» до сих пор присутствует в классификации задач:
линейное программирование;
квадратичное программирование;
выпуклое программирование;
целочисленное программирование;
и т.д.
04.12.2012
Слайд 15- площадь поверхности коробки с банками.
Пример №1. Дизайн коробки.
Общее описание.
При конструировании некоторых объектов, систем либо структур, их параметры должны
удовлетворять определенным условиям и ограничениям, налагаемыми свойствами конструкции. Необходим выбор независимых переменных, от которых зависит конечный продукт, таких как себестоимость, вес и т.д.Искусственный пример.
Надо рассчитать параметры консервной банки заданного объема так, чтобы минимизировать общую стоимость коробки с 12-ю банками, уложенными по формуле 3x4.
Цена рассчитывается как сумма:
, где
- площадь поверхности 12-ти банок, а
04.12.2012
Слайд 16Пример №1. Дизайн коробки.
Общее ограничение. Сторона ящика не может превышать
заданной величины
Параметры конструкции:
- радиус,
- высота банки;
Ограничение на объем:
Боковая поверхность:
Размеры коробки:
Боковая
поверхность коробки:Ограничение размеров:
Положительность ограничений:
04.12.2012
Слайд 17Пример №1. Дизайн коробки.
Резюме. Искомыми переменными являются радиус и высота
банки. Их множество допустимых значений описывается ограничениями:
где
и, следовательно,
исходные данные (константы).
Хотя неравенства
Первые пять условий – ограничения-неравенства, шестое – ограничение-равенство. На множестве допустимых значений надо минимизировать функцию:
Величины
не являются «ограничениями» задачи.
04.12.2012
Слайд 18Пример №1. Дизайн коробки.
Напомним, требуется определить радиус основания и высоту
консервной банки заданного объема так, чтобы минимизировать общую стоимость коробки
с 12-ю банками, уложенными в 4 ряда по три коробки в каждом ряду.на множестве допустимых значений переменных, заданном ограничениями:
Математическая формулировка. Минимизировать функцию:
где
04.12.2012
Слайд 19Пример №1. Подробное рассмотрение
Избыточные ограничения. Очевидно, что ограничение
слабее уже имеющихся.
Оно
может быть без ущерба опущено. Однако в реальных задачах распознавание
избыточных ограничений может оказаться не менее сложной проблемой, чем решение исходной задачи оптимизации.Неактивные ограничения. Оптимальное решение
(единственное?) может удовлетворять одному или всем условиям-неравенствам как строгим неравенствам.
Это неактивные ограничения. Они могут быть без ущерба опущены. Иногда может помочь предварительный отбор неактивных ограничений. И во многих численных приложениях это основная и очень сложная проблема.
04.12.2012
Слайд 20Пример №1. Подробное рассмотрение
Избыточные переменные. Конечно же, возможно
разрешить уравнение
и «упростить»
задачу – оставить лишь одно неизвестное. Но, кроме того, что
такой прием может быть полезен в данном конкретном случае, переход к меньшему числу переменных может ухудшить остальные ограничения.Неравенства или равенства? Ограничение
может быть записано в виде
Задача такова, что оптимум все равно достигается при условии равенства. А неравенство определяет выпуклое множество допустимых значений, в то время как равенство – нет.
относительно
, не влияя ни на
что, кроме решения.
04.12.2012
Слайд 21Пример №1. Подробное рассмотрение
Выпуклость. Даже с учетом последних формулировок задача
не становится «выпуклой», поскольку сама целевая функция не выпукла.
Урок
заключается в том, что формулировка задачи требует творческого подхода и опыта при учете важных свойств, необходимых для аккуратного решения проблемы оптимизации. 04.12.2012