Автоматическая поддержка целостности по ссылкам

подчиненные записи либо соответствующим образом изменить значения FK для этих

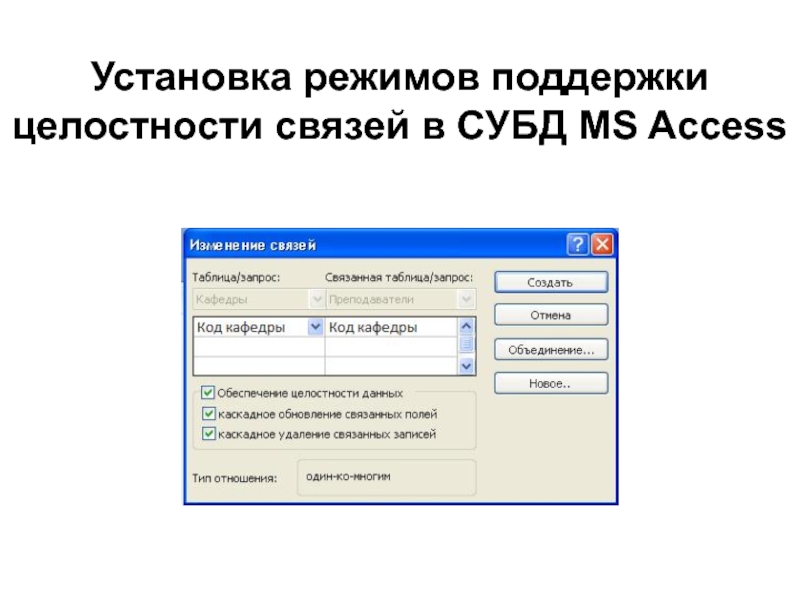
записей

б) во всех подчиненных записях, которые ссылаются на удаляемую запись, присвоить неопределенное значение внешнему ключу (FK)

в) одновременно с удалением записи из главной таблицы удалить все подчиненные записи, которые ссылаются на удаляемую запись (каскадное удаление)

(РИ) – это инструменты для манипулирования табличными данными в реляционных

БД.
В частности, любой запрос к БД можно записать в виде некоторой формулы РА или некоторого выражения (предиката) РИ.
Средства РА и РИ эквивалентны между собой, однако отличаются уровнем (степенью) процедурности.

всегда является таблица (свойство замкнутости на таблицы).
Формулы РА, состоящие из

отдельных операндов и операций, имеют четко выраженную процедурность, т.к. результат запроса, который записан в виде формулы РА, вычисляется при поочередном выполнении элементарных операций.

РА – это теоретический язык операций, которые позволяют получить на основе одной или нескольких таблиц другую таблицу.

должен удовлетворять результат запроса.
Поэтому средства РИ являются непроцедурными или декларативными

(описательными), т.к. они всего лишь описывают свойства желаемого результата.

DML (Data Manipulation Language) для существующих СУБД.
К примеру, язык SQL

с точки зрения пользователя является непроцедурным языком, т.к. при записи запроса на этом языке в первую очередь указываются источники данных и условия, которым должен удовлетворять требуемый результат.
С другой стороны, при выполнении запроса на уровне СУБД реализуется некоторая процедура с использованием операций РА.

отдельная запись – это множество значений атрибутов.
Следовательно, традиционные операции, которые

применяются в теории множеств, пригодны для манипулирования табличными данными в реляционных БД.
Дополнением к этому являются специальные операции, которые нужны для работы с базами данных.

1972 г.

произведение (Cartesian product);
объединение таблиц (union);
разность таблиц (difference).
Остальные операции – дополнительные:
соединение

(join);
пересечение (intersection);
деление (division).
Каждую из дополнительных операций можно выразить в терминах пяти основных.

которой каждая запись принадлежит либо таблице Х, либо таблице Y.
Таблицы

Х и Y должны быть совместимыми:
одинаковое число атрибутов;
соответствующие атрибуты имеют одинаковый домен.

которой каждая запись принадлежит таблице Х, но не принадлежит таблице

Y.
Таблицы Х и Y должны быть совместимыми.

R, в которой каждая запись принадлежит как таблице Х, так

и таблице Y.

Выражение (X–Y) дает записи из Х, которых нет в Y. Тогда из тождества X∩Y=X–(X–Y) вытекает, что операция пересечения является производной от операции разности.

которой все записи получены как неповторяющиеся сцепления одной записи из

таблицы Х и одной записи из таблицы Y.
Ограничений на структуру таблиц Х и Y нет.

удаления из таблицы Х всех атрибутов, которые не входят в

заданный список.
Повторяющиеся записи исключаются.

R только те записи из таблицы Х, которые удовлетворяют заданному

условию.

разных таблицах и характеризуются определенными логическими связями.
Операция соединения имеет несколько

разновидностей.

1. Естественное соединение: R=X▷◁Y

Из таблиц Х и Y связываются записи, которые имеют равные значения в общих (одноименных) столбцах.
В таблице R каждый из общих столбцов остается в единственном экземпляре.

записи, в которых значения для определенных столбцов удовлетворяют заданному условию

Θ.
Условие Θ записывается в виде логического выражения, в котором могут присутствовать следующие операторы сравнения: =, <>, <, >, <=, >=.

X ▷◁Θ Y = σΘ(X × Y)

Если в выражении Θ используется только условие равенства (=), то Θ-соединение называют эквисоединением.

естественное соединение, но в таблицу R попадают даже те записи

из таблицы Х, для которых не подходит ни одна из записей в таблице Y.
Следовательно, в таблицу R включаются абсолютно все данные из таблицы Х.

Для этой операции существует несколько разновидностей.

таблицу R попадают даже те записи из таблицы Y, для

которых не подходит ни одна из записей в таблице Х.
Следовательно, в таблицу R включаются абсолютно все данные из таблицы Y.
Полное внешнее соединение: R=X ⊃⊂ Y
Формируется как объединение результатов левого и правого внешних соединений для таблиц Х и Y:
X ⊃⊂ Y = (X ⊃◁Y) ∪ (X▷⊂ Y)

2518
Вариант 2
A := σPROD_ID=2518(SALES)
R := ΠCUST_NAME(CUSTOMERS▷◁ A)
Для варианта 2 кардинальность

таблицы А значительно меньше, чем у таблицы SALES.
Следовательно, в этом случае операция соединения выполняется существенно быстрее.

Вариант 1
A := CUSTOMERS▷◁ SALES
R := ΠCUST_NAME( σPROD_ID=2518(A) )

σPROD_NAME=“XXXXX”(PRODUCTS)
B := SALES ▷◁ A
R := ΠCUST_NAME(CUSTOMERS▷◁ B )