Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
16.12.2019 1 Теория вероятностей и математическая статистика Лекции 1 курс
Содержание
- 1. 16.12.2019 1 Теория вероятностей и математическая статистика Лекции 1 курс
- 2. Теория вероятностей Тема 2. Случайные величины.
- 3. Случайные величиныСлучайной величиной Х в данном опыте
- 4. Например,a) Х - оценка на экзаменеСовокупность значений
- 5. Функция распределения случайной величиныФункцией распределения F(x) случайной
- 6. Вероятность попадания случайной величины в промежуток и в точку Основное свойство функции распределения Р(X
- 7. Действительно:
- 8. Дискретная случайная величинаСлучайная величина Х называется дискретной,
- 9. Законом распределения дискретной случайной величины Х является
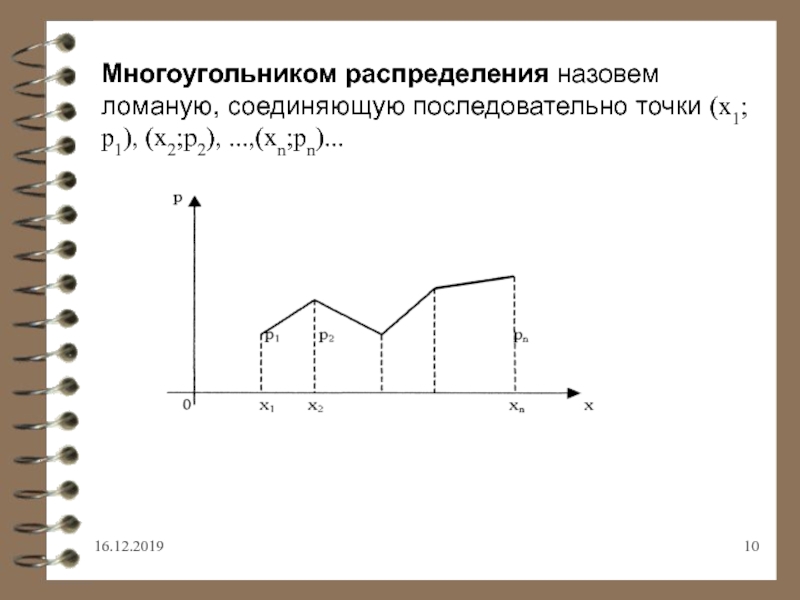
- 10. Многоугольником распределения назовем ломаную, соединяющую последовательно точки (х1;р1), (х2;р2), ...,(хn;рn)...
- 11. Пример 15:Среди шести микроскопов два изношенных. Составить
- 12. Случайная величина Х может принимать значения:
- 13. Если x (-;0], то F(x)=P(X
- 14. Итак,
- 15. Основные числовые характеристики случайной величины
- 16. Простейшие свойства математического ожидания.Свойство 1. Математическое ожидание
- 17. Слайд 17
- 18. Слайд 18
- 19. Простейшие свойства дисперсииСвойство 1. Дисперсия постоянной величины
- 20. Пример . Найти дисперсию случайной величины Х, имеющей следующий закон распределения
- 21. Пример . Найти дисперсию случайной величины Х, имеющей следующий закон распределения
- 22. Скачать презентанцию
Теория вероятностей Тема 2. Случайные величины. Функция распределения и ее свойства. Дискретная случайная величина. Ряд распределения. Числовые характеристики.
Слайды и текст этой презентации
Слайд 2Теория вероятностей
Тема 2.
Случайные величины.
Функция распределения
и ее свойства. Дискретная случайная величина.
Слайд 3Случайные величины
Случайной величиной Х в данном опыте называется переменная величина,
которая в результате испытания примет одно из своих возможных значений,
но какое именно до проведения опыта неизвестно. Совокупность всех возможных значений случайной величины может бытьДискретной - все возможные значения случайной величины образуют конечную или бесконечную последовательность (отдельные точечные значения).
Непрерывной - все значения случайной величины заполняют сплошь некоторый промежуток.
Слайд 4Например,
a) Х - оценка на экзамене
Совокупность значений дискретная -{2,3,4,5}
б) Х
- время безотказной работы двигателя (ресурс)
Совокупность значений непрерывная, любое значение
из промежутка [0,t] (t - момент отказа двигателя).
Слайд 5Функция распределения случайной величины
Функцией распределения F(x) случайной величины Х называется
вероятность того, что случайная величина Х в результате испытания примет
значение, меньшее х, т.е.F(x)=P(X
1) область определения F(x) - интервал (-
2) 0 < F(x) 1,
3) F(-)=0, т.к. P(X<- )=P()=0,
4) F(+)=1, т.к. P(X<+ )=P()=1,
5) F(x)- неубывающая функция.
Будем считать, что F(x) непрерывна слева
Слайд 6Вероятность попадания случайной величины в промежуток и в точку
Основное
свойство функции распределения
Р(X
равна разности значений функции распределения в концах интервалаСледствие:
Р(Х=) =
Слайд 8Дискретная случайная величина
Случайная величина Х называется дискретной, если ее совокупность
ее значений дискретна.
Законом (рядом) распределения случайной величины Х называется
любая ее вероятностная характеристика, из которой можно получить функцию распределения F(x).
Слайд 9Законом распределения дискретной случайной величины Х является ряд распределения, т.е.
перечисление всех возможных значений Х и их соответствующих вероятностей:
рi=P(X=xi), где
i=1;2;...;n;...Т.к. события (X=x1), (X=x2),...,(X=xn),... образуют полную группу событий и несовместны, то:
Слайд 10Многоугольником распределения назовем ломаную, соединяющую последовательно точки (х1;р1), (х2;р2), ...,(хn;рn)...
Слайд 11Пример 15:
Среди шести микроскопов два изношенных.
Составить ряд распределения случайной
величины Х- числа изношенных микроскопов среди трех наудачу отобранных.
Найти
функцию распределения F(x) и построить ее график. 
Слайд 12 Случайная величина Х может принимать значения: 0;1;2.
Р(Х=0)=
Р(Х=1)=
Р(Х=2)=
Условие нормировки: 0,2+0,6+0,2=1.
![Если x (-;0], то F(x)=P(X](/img/thumbs/9090b4c305d29e9f152cd3a15c862437-800x.jpg "16.12.2019
1
Теория вероятностей и математическая статистика
Лекции 1 курс Если x (-;0], то F(x)=P(X")
Слайд 14Итак,
Зная F(x), можно, например, найти Р(Х=3)=0,
т.к. х=3- точка непрерывности
F(x); или найти Р(Х=1)=0,8-0,2=0,6, т.к. х=1- точка разрыва F(x); или P(-1
Слайд 16Простейшие свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной величины равно
самой постоянной, т.е.
М(C)=С.
Свойство 2. Постоянный множитель можно выносить за знак
математического ожидания, т.е. М(СX)=С(MX).
Пример . Дано:
X -3 -1 2
P 0,2 0,5 0,3
Найти М[5X].
Решение.
М[5X]=5M[X], т.к. M[X]=(-3)0,2+(-1)0,5+20,3=-0,5, то М[5X]=5(-0,5)= -2,5.
Слайд 19Простейшие свойства дисперсии
Свойство 1. Дисперсия постоянной величины равна нулю.
D(C)=0
Свойство 2.
Постоянный множитель можно выносить за знак дисперсии, возводя его при
этом в квадрат, т.е.D(СX)=С2(DX).
