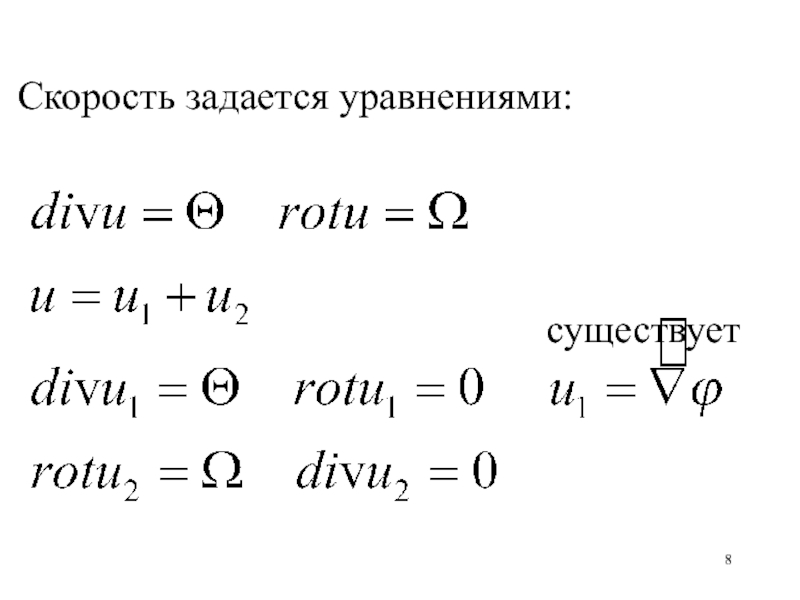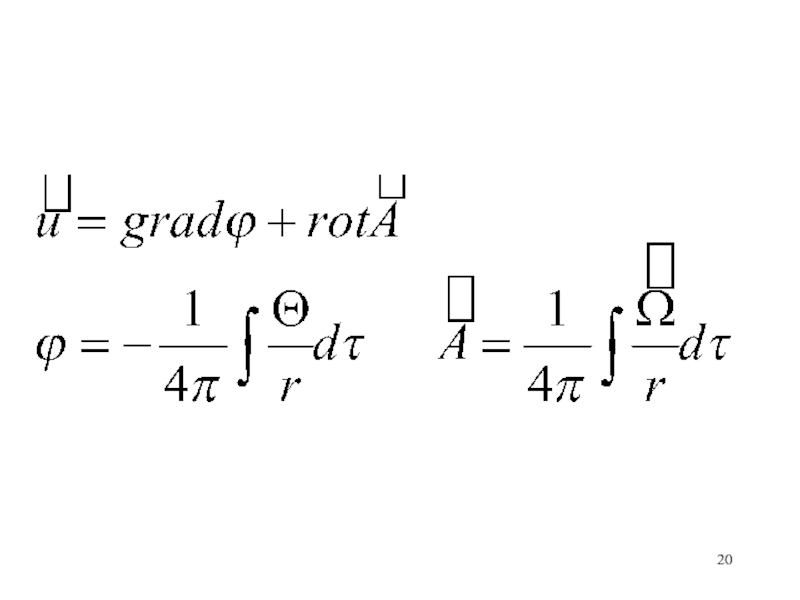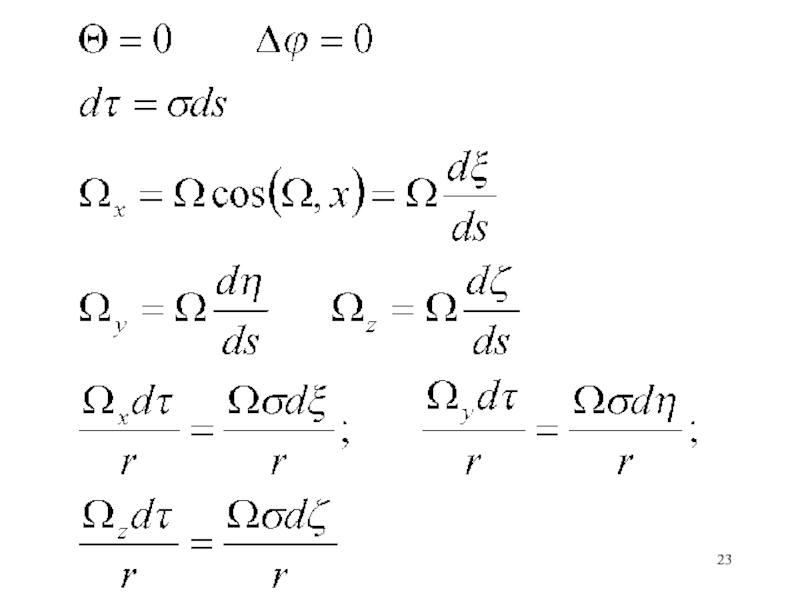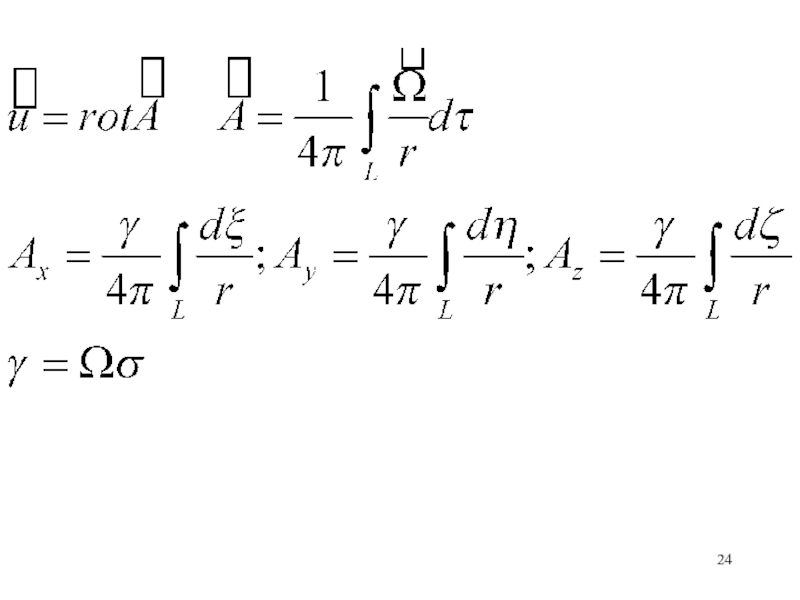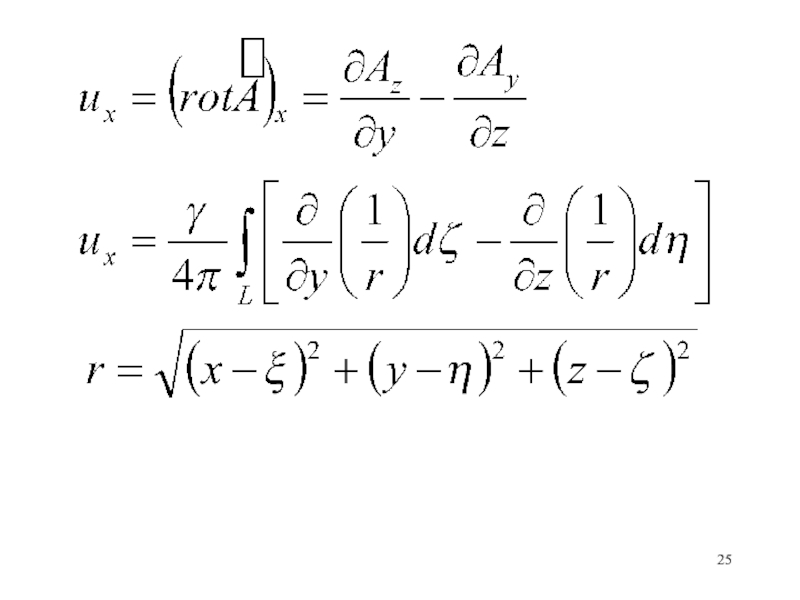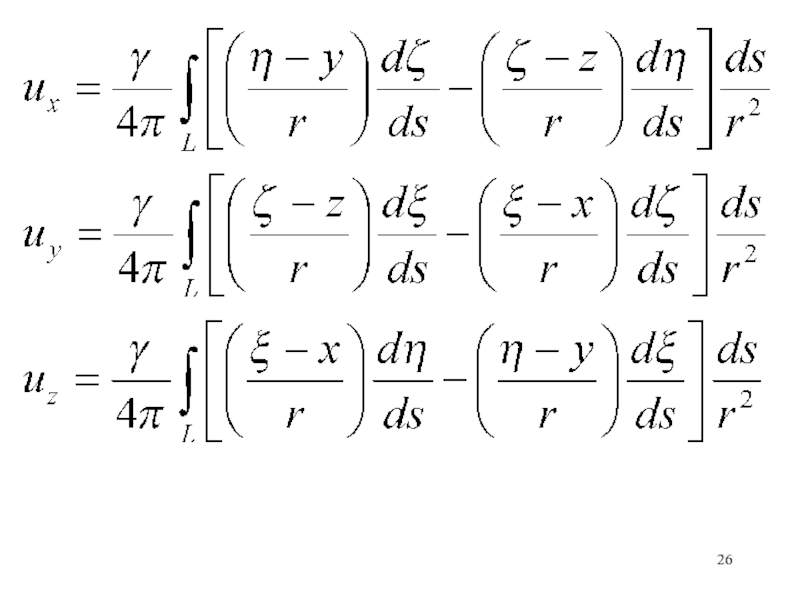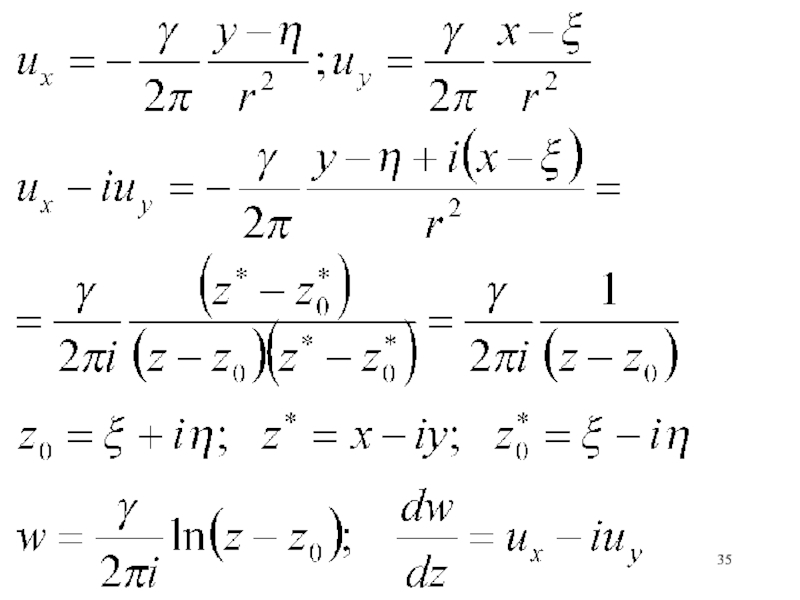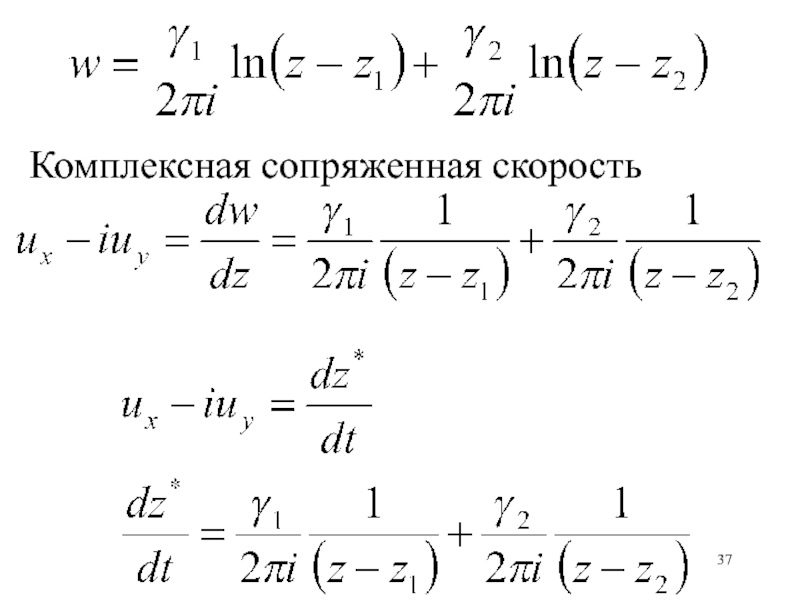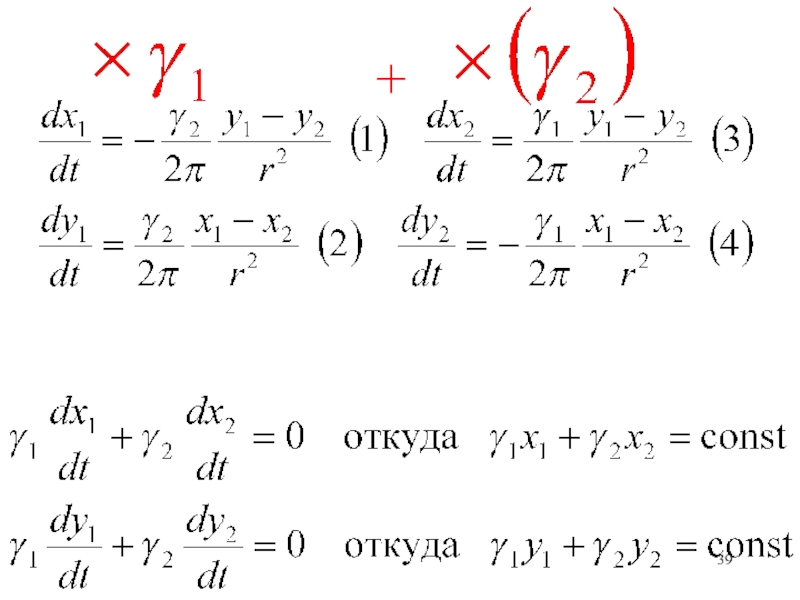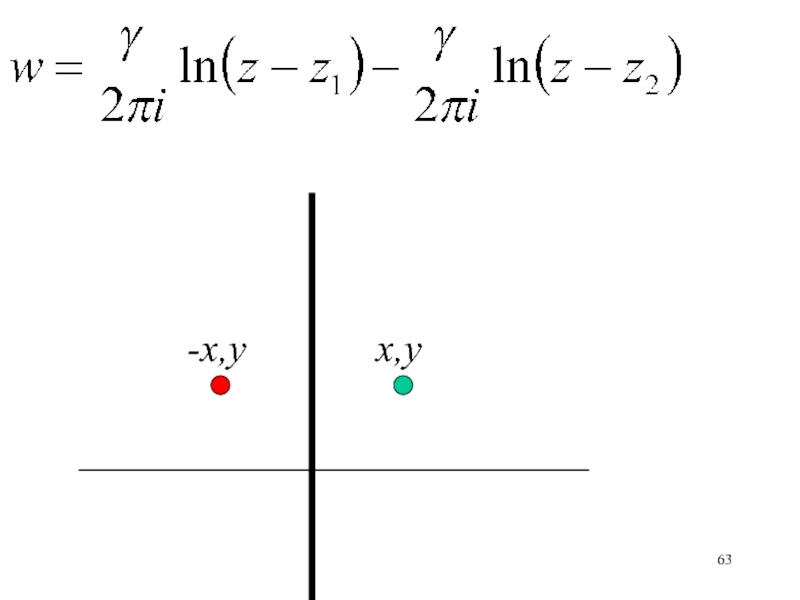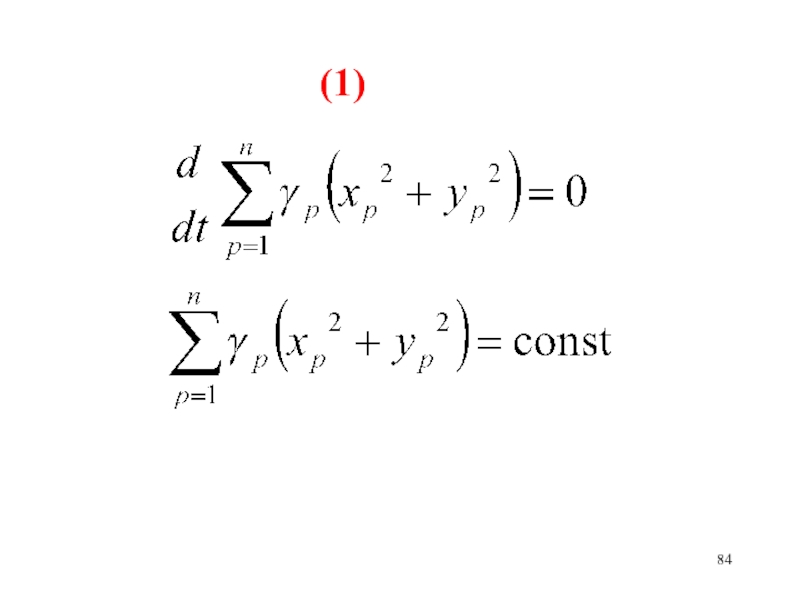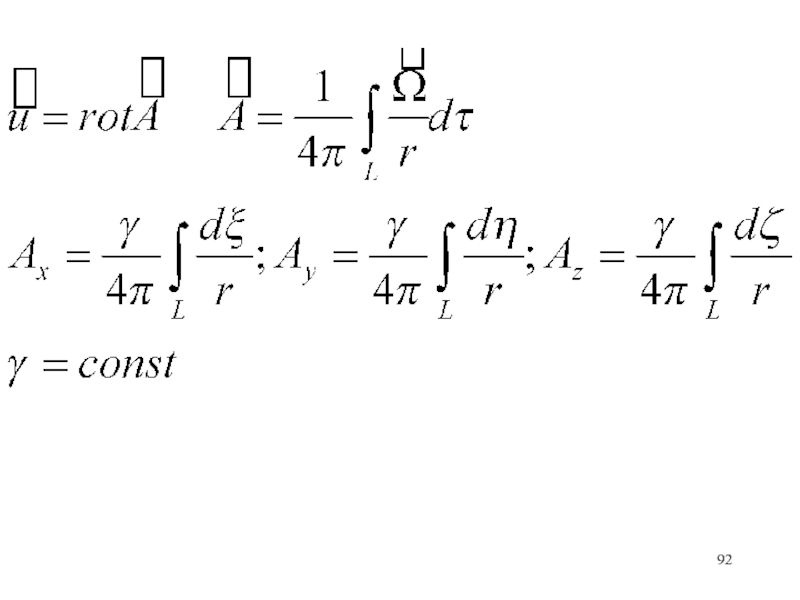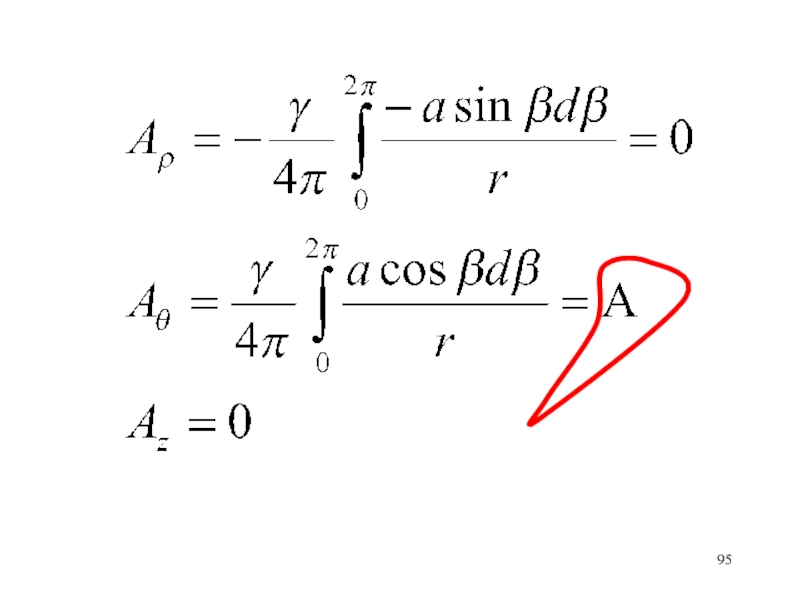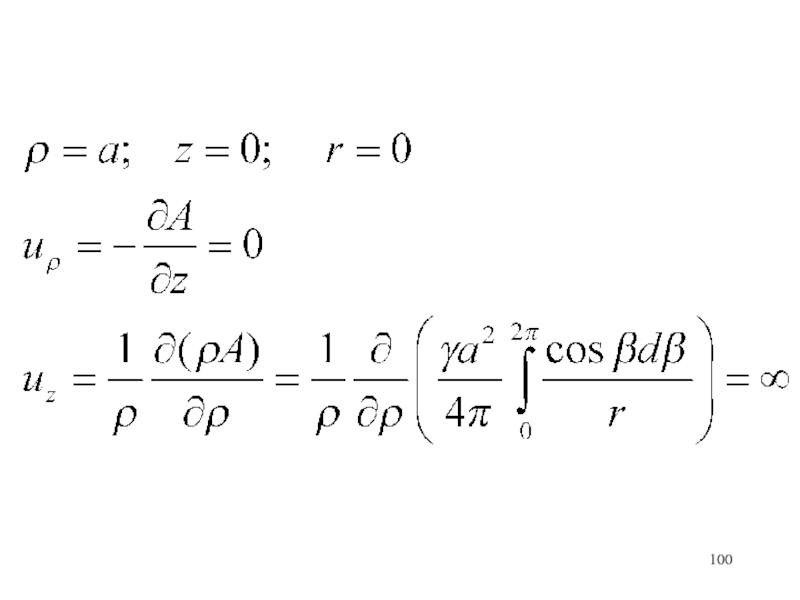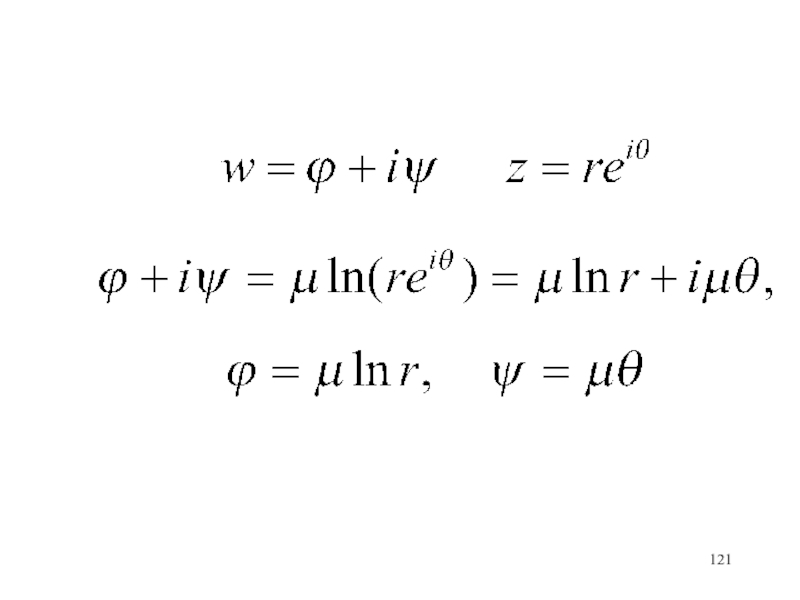Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Эйлер, Ляпунов, Навье и Стокс
Содержание
- 1. 1 Эйлер, Ляпунов, Навье и Стокс
- 2. Поле скорости по заданному полю вихрей и расхождения скорости
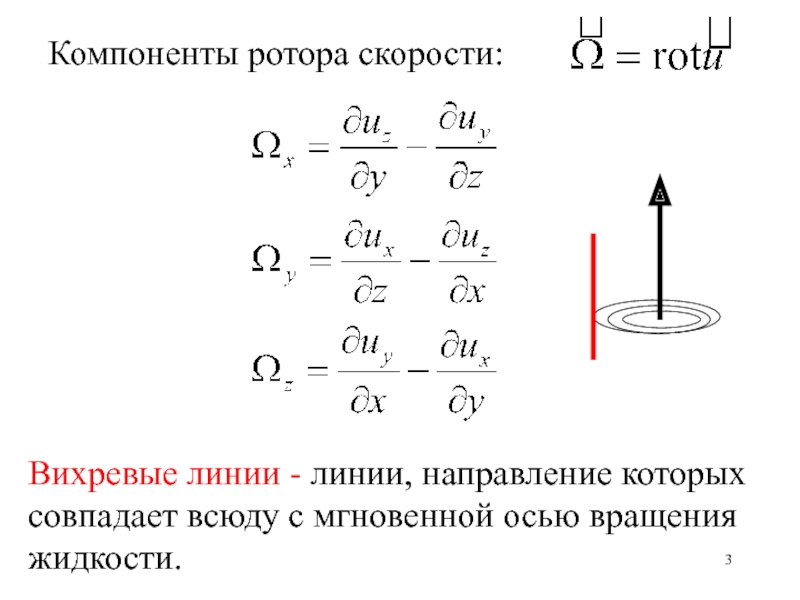
- 3. Компоненты ротора скорости:Вихревые линии - линии, направление которых совпадает всюду с мгновенной осью вращения жидкости.
- 4. Дифференциальное уравнение вихревых линийЕсли через каждую точку
- 5. ЗадачаЗаданы распределения вихря и дивергенции скорости
- 6. ПредположенияЖидкость заполняет все пространство, находится в покое
- 7. 5. На поверхностях разрыва нормальная составляющая Ω
- 8. Скорость задается уравнениями:существует
- 9. Для определения u1 получаем уравнение ПуассонаПредположим, что
- 10. По теореме ГауссаТ.е. объемный интеграл от расхождения
- 11. Пусть τ→0. Получаем картину течения от точечного
- 12. φ – функция только r, в сферических координатах нет зависимости от широты и долготы.Интегрируем:
- 13. Произвольная постоянная определяется из условия, что поток
- 14. Получаем:Произвольная постоянная не влияет на величину скорости течения и может быть отброшена
- 15. Предположим, что интенсивность источника имеет значение qВ этом случае
- 16. Если задано распределение источников Θ(ξ, η, ζ)Где
- 17. Решение системы
- 18. Определим вектор u2 для системыУдовлетворим второму уравнению, если положимгде А – векторный потенциал. ТогдаМожно доказать тождество:
- 19. Получаем уравнение:(Можно считать не нарушая общности)
- 20. Слайд 20
- 21. Одна вихревая нитьНесжимаемая жидкость, покоящаясяна бесконечности
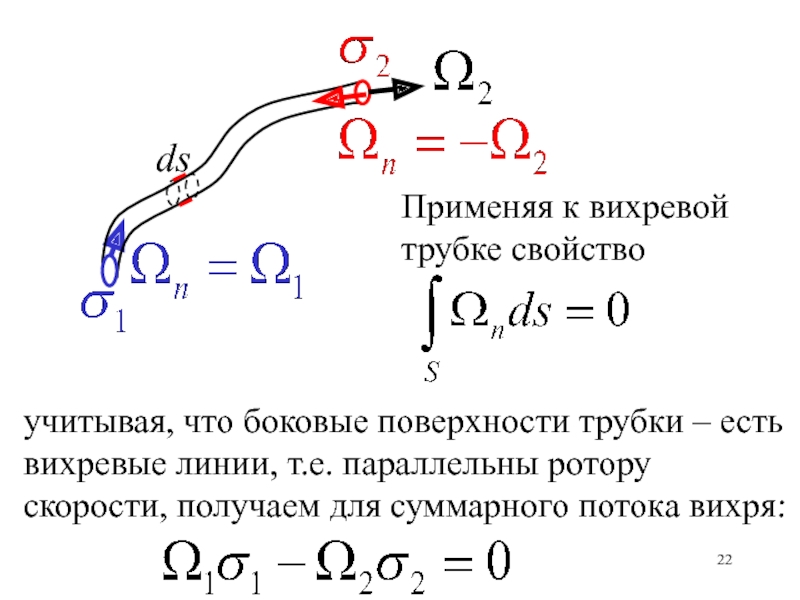
- 22. Применяя к вихревой трубке свойствоучитывая, что боковые
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
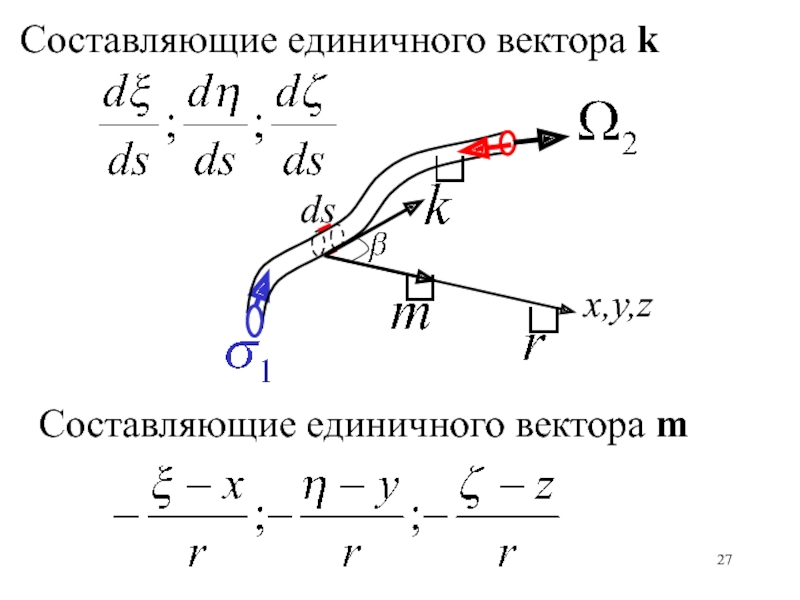
- 27. dsx,y,zСоставляющие единичного вектора kСоставляющие единичного вектора m
- 28. Вклад в величину скорости в точке (x,y,z) от элемента вихревой трубки ds определяется выражением:
- 29. Электродинамика:Сила, действующая на магнитный полюс в точке
- 30. Прямолинейныевихриплоское движениенесжимаемая жидкость
- 31. Пусть движение происходит в плоскости х, у.
- 32. Скорость жидкости в точке (х, у) определяется:Считая ξ, η, (х, у, z) постоянными, интегрируем
- 33. Достаточно рассматривать движение на плоскости 0xy, причем
- 34. Найти комплексный потенциал для точечного вихря.
- 35. Слайд 35
- 36. 2 вихряДве параллельные прямые вихревые нити
- 37. Комплексная сопряженная скорость
- 38. Скорость первого вихря в точке z1 (сам
- 39. +
- 40. Получаем интеграл движения центра инерции системы двух
- 41. Вычитаем из первого третье уравнение, из второго – четвертое.
- 42. Интегрируем и получаем:Расстояние между вихрями не меняется в процессе перемещения
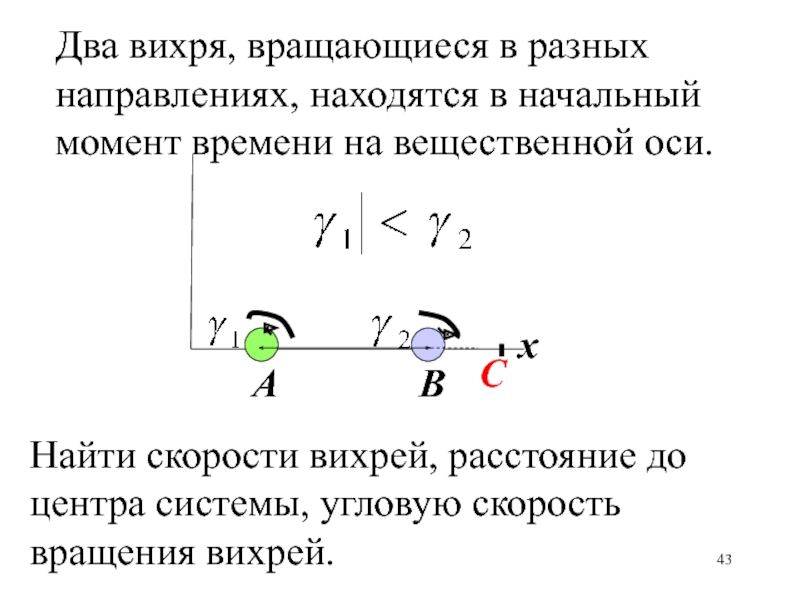
- 43. ABxСДва вихря, вращающиеся в разных направлениях, находятся
- 44. Вихревая нить с координатами
- 45. ABxyСС
- 46. Угловая скорость вращения вихрей вокруг центра СГде будет точка С, если вихри вращаются в одном направлении?
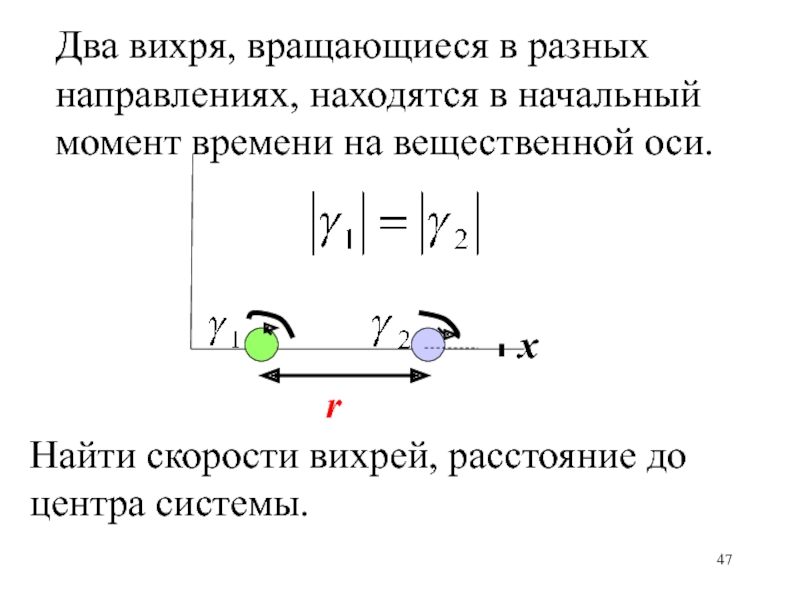
- 47. xrДва вихря, вращающиеся в разных направлениях, находятся
- 48. Скорость первого вихря в точке z1 (сам
- 49. Отделяем вещественную часть от мнимой :Вихри перемещаются
- 50. Пример 1Одна вихревая нить в точке (х,у),
- 51. хуrЦентр одиночного вихря не смещается во времени.
- 52. Пример 2Внутри круга радиуса а жидкость вращается
- 53. хуrНа границе вихря скорость равна a.а
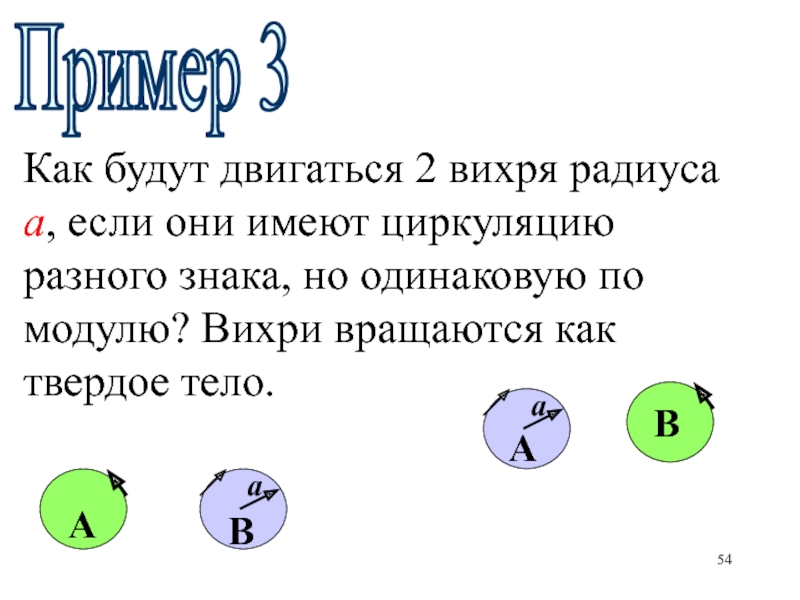
- 54. Как будут двигаться 2 вихря радиуса а,
- 55. Движение двух вихрей с противоположным направлением вращения иСААС=V1=V2=Вихри двигаются по прямой с одинаковой скоростьюаВ
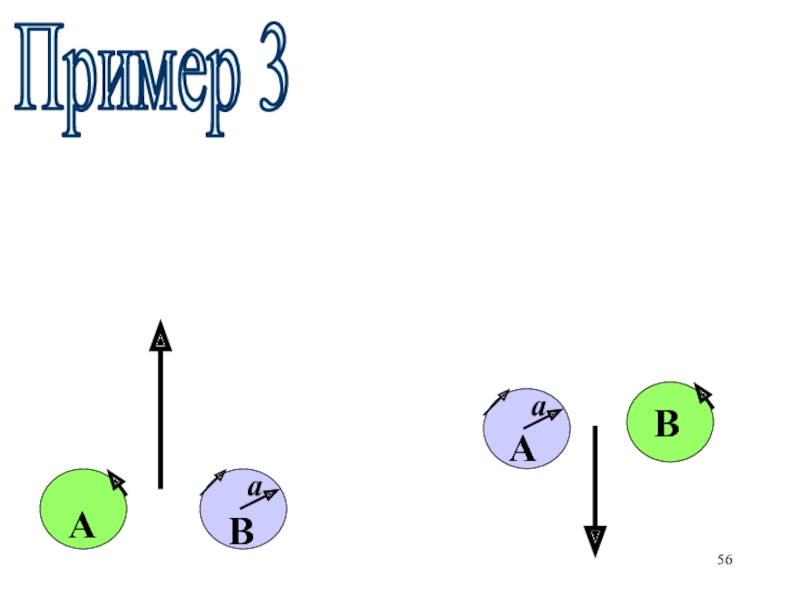
- 56. Пример 3АаВаАВ
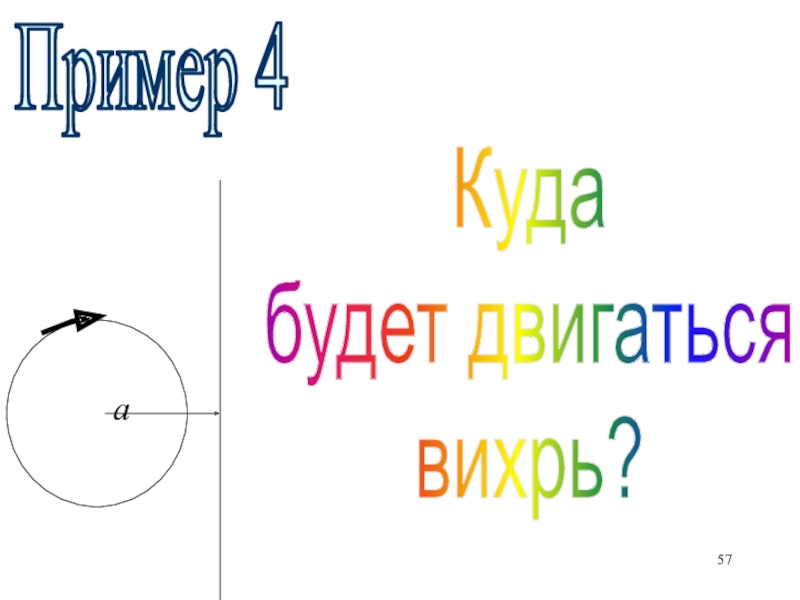
- 57. аКудабудет двигатьсявихрь?Пример 4
- 58. Найти скорость перемещения вихря у твердой стенки
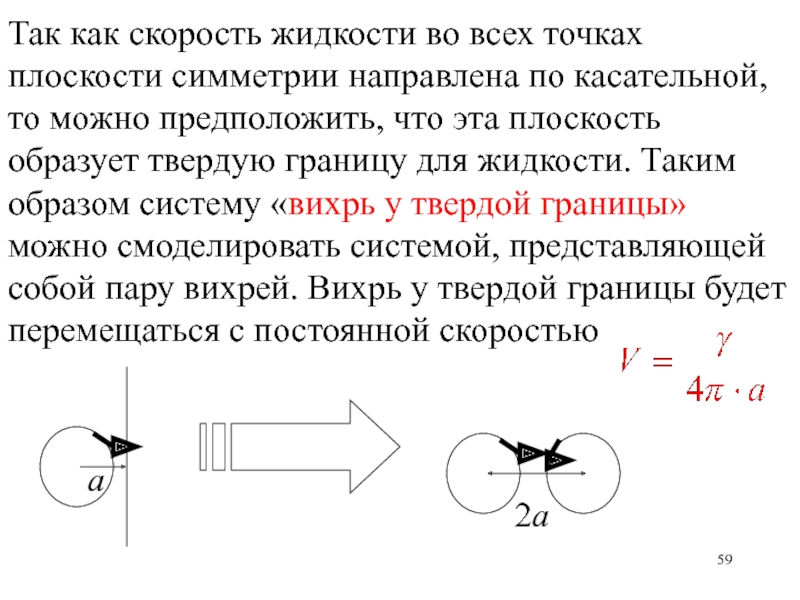
- 59. Так как скорость жидкости во всех точках
- 60. Пример 5В точке с координатами х,у находится
- 61. x,y
- 62. Так как циркуляция скорости вихря постоянна, то
- 63. x,y-x,y
- 64. Для того, чтобы описать влияние стенки, расположенной
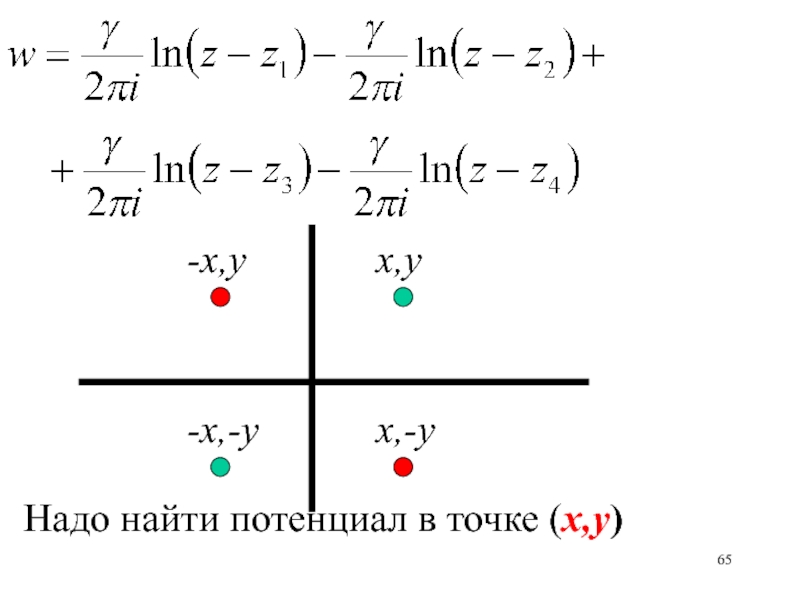
- 65. x,y-x,yx,-y-x,-yНадо найти потенциал в точке (x,y)
- 66. На линии тока =const, т.е.
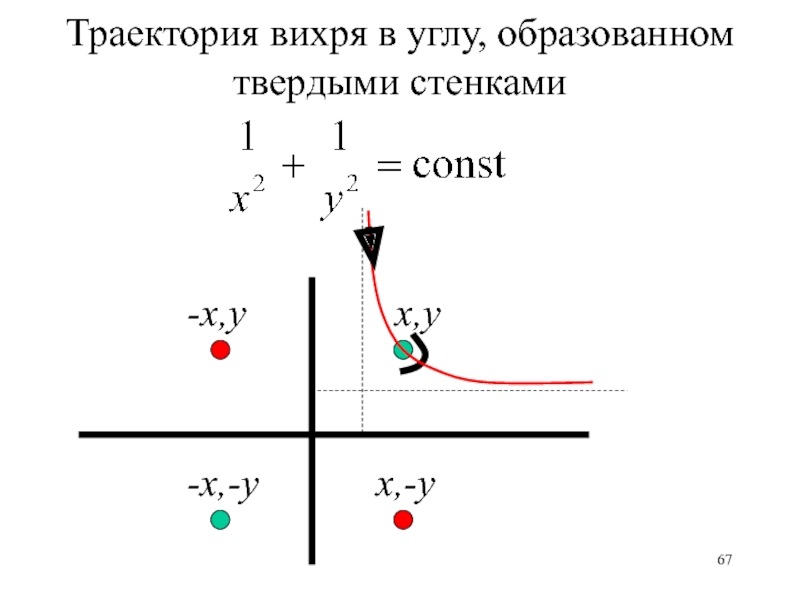
- 67. x,y-x,yx,-y-x,-yТраектория вихря в углу, образованном твердыми стенками
- 68. Слайд 68
- 69. Слайд 69
- 70. Слайд 70
- 71. Слайд 71
- 72. Слайд 72
- 73. Слайд 73
- 74. Слайд 74
- 75. Слайд 75
- 76. Слайд 76
- 77. Слайд 77
- 78. расположенных в точках z1,…, zn и имеющих
- 79. Уравнение движения вихря в точке zp (k=p)Умножая
- 80. СледовательноПолучаемОтделяем мнимую и действительную части
- 81. Если
- 82. Следствие 2
- 83. Сумма моментов количеств движения масс p относительно начала координат не меняется со временем(1)(2)(2)
- 84. (1)
- 85. Сумма моментов инерции масс p относительно начала координат не меняется со временем
- 86. Умножая выражения скорости наи суммируя по переменной
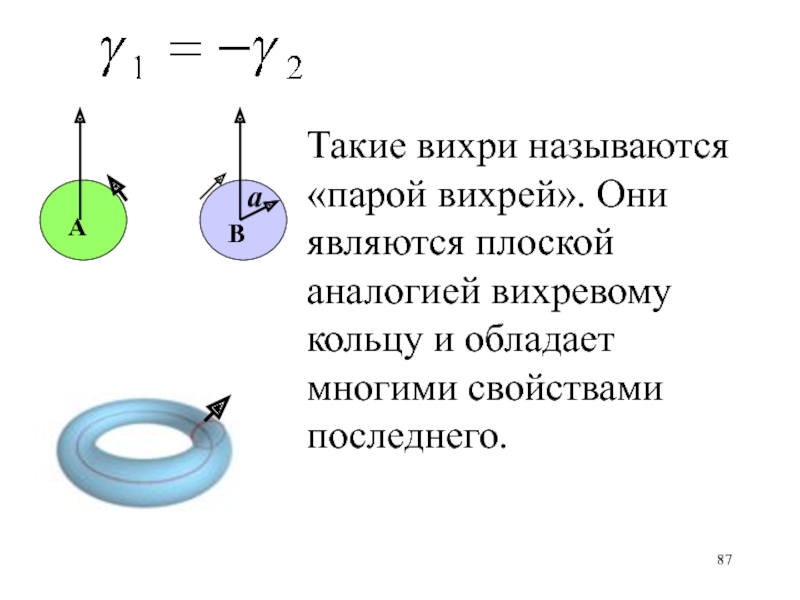
- 87. АаВТакие вихри называются «парой вихрей». Они являются плоской аналогией вихревому кольцу и обладает многими свойствами последнего.
- 88. Куда двигается кольцевой вихрь?
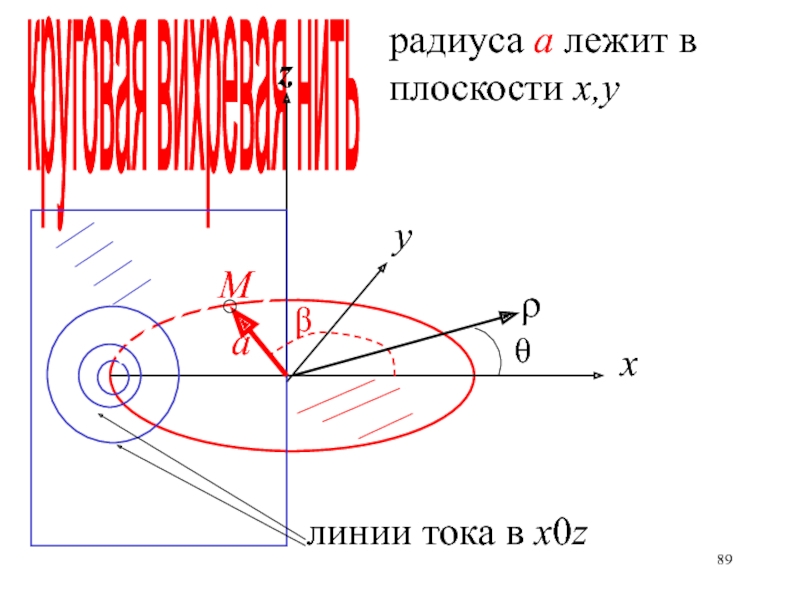
- 89. круговая вихревая нитьрадиуса а лежит в плоскости х,у
- 90. Координаты точки М на вихревой нити в
- 91. (1)Запишем компоненты скорости через векторный потенциал
- 92. Слайд 92
- 93. Для векторного потенциала в точке x,y,z
- 94. Для плоскости x,y при θ=0Вследствие симметрии задачи это справедливо для всех углов θ
- 95. Слайд 95
- 96. Подставляем выражения векторного потенциала в (1) и находим компоненты скорости
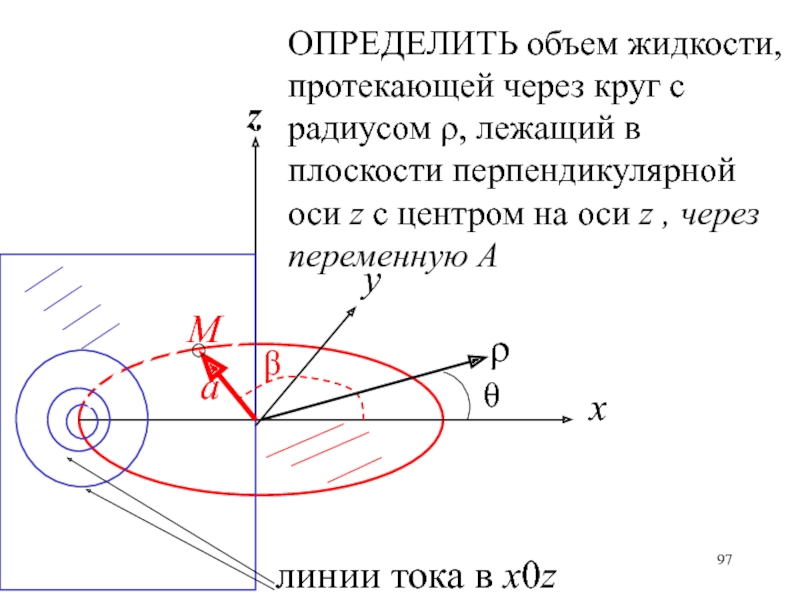
- 97. ОПРЕДЕЛИТЬ объем жидкости, протекающей через круг с
- 98. Объем жидкости, протекающей через круг с радиусом
- 99. ОПРЕДЕЛИТЬскорость перемещения круговой вихревой нити
- 100. Слайд 100
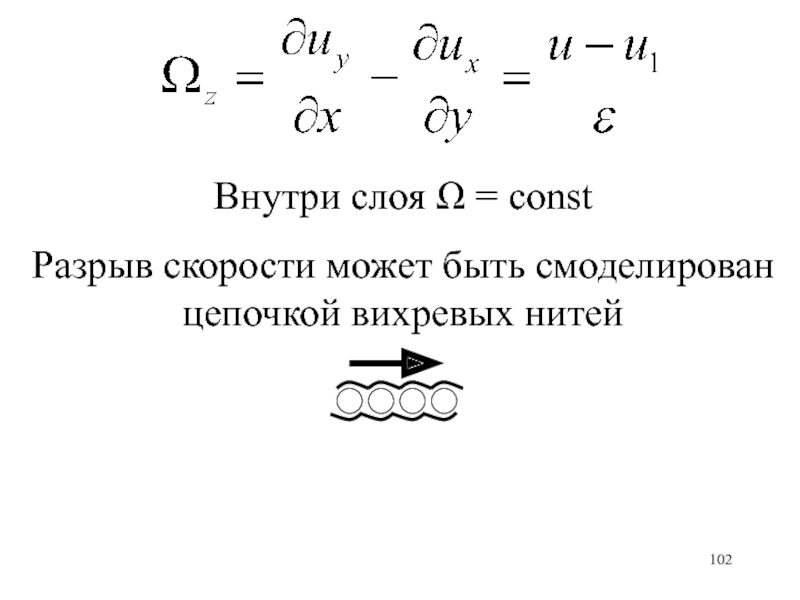
- 101. Вихревой слой0аSS1xyu1uНайти ротор скорости
- 102. Внутри слоя = constРазрыв скорости может быть смоделирован цепочкой вихревых нитей
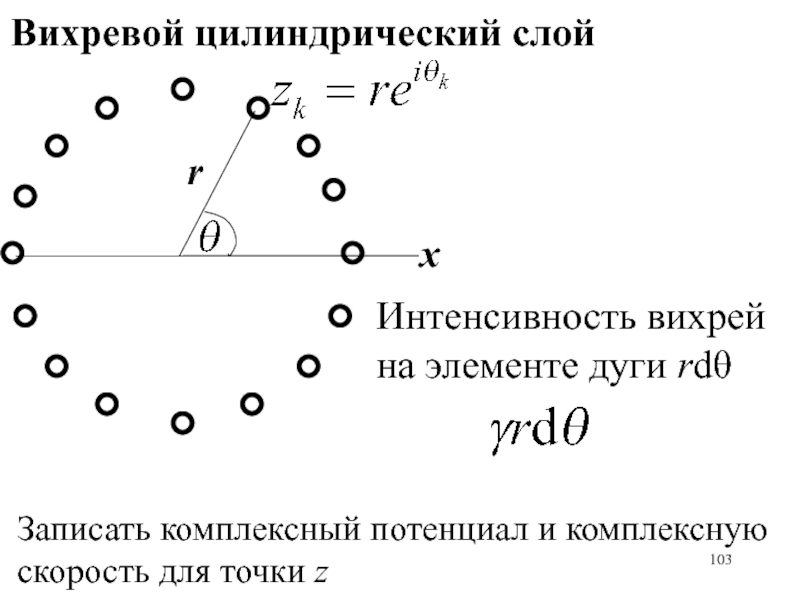
- 103. Вихревой цилиндрический слойxrИнтенсивность вихрей на элементе дуги rdЗаписать комплексный потенциал и комплексную скорость для точки z
- 104. Комплексный потенциал цилиндрического слоя в точке zКомплексная скоростьДелим подинтегральное выражение на z, умножаем на
- 105. z рассматривается как постоянная при интегрировании
- 106. Если z внутри окружности, т.е.При изменении
- 107. Если z вне окружности, т.е.При изменении
- 108. Комплексная скоростьдвижения нет внутри цилиндравне цилиндра движение
- 109. 2 3КОНТРОЛЬНАЯ РАБОТА
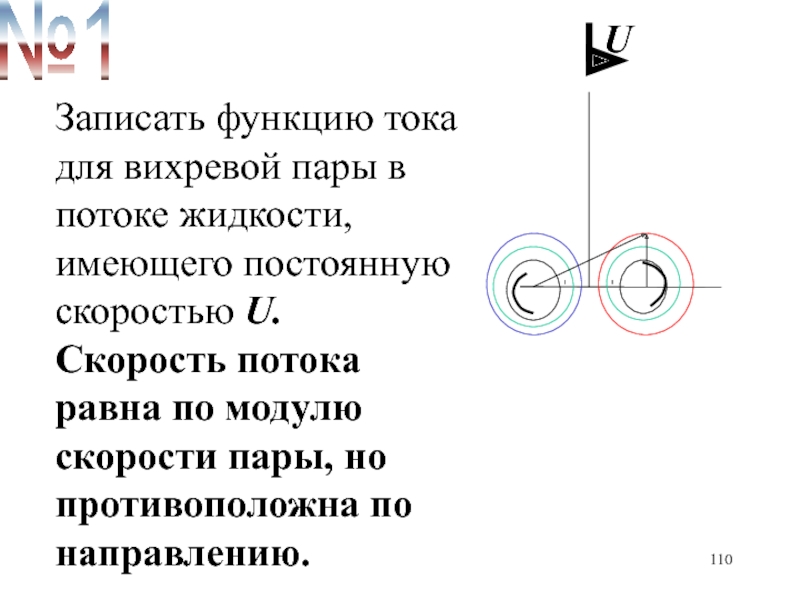
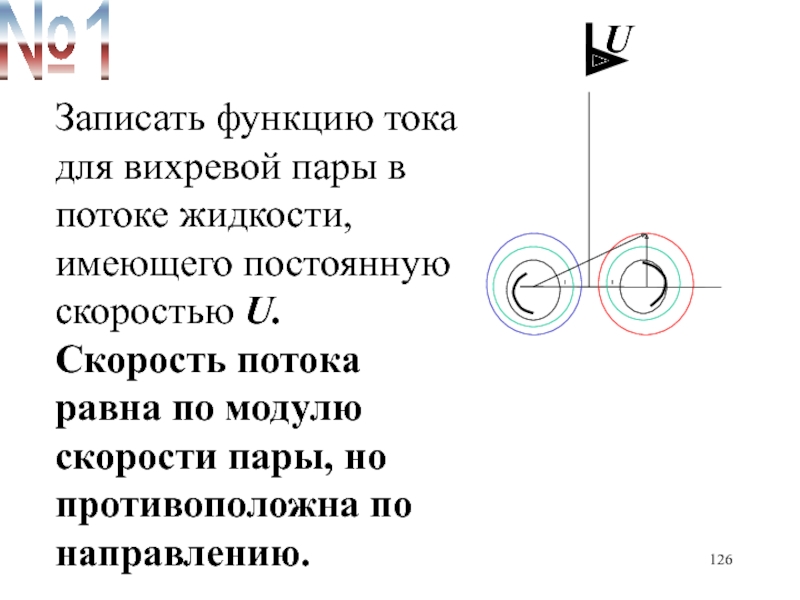
- 110. UЗаписать функцию тока для вихревой пары в
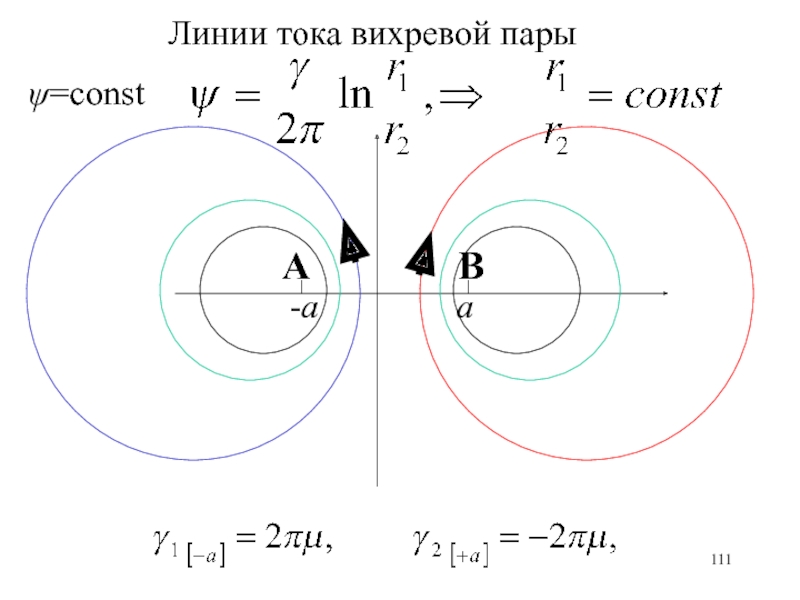
- 111. =constЛинии тока вихревой парыАВ
- 112. Функция тока для течения, имеющего постоянную скорость вдоль оси ординат
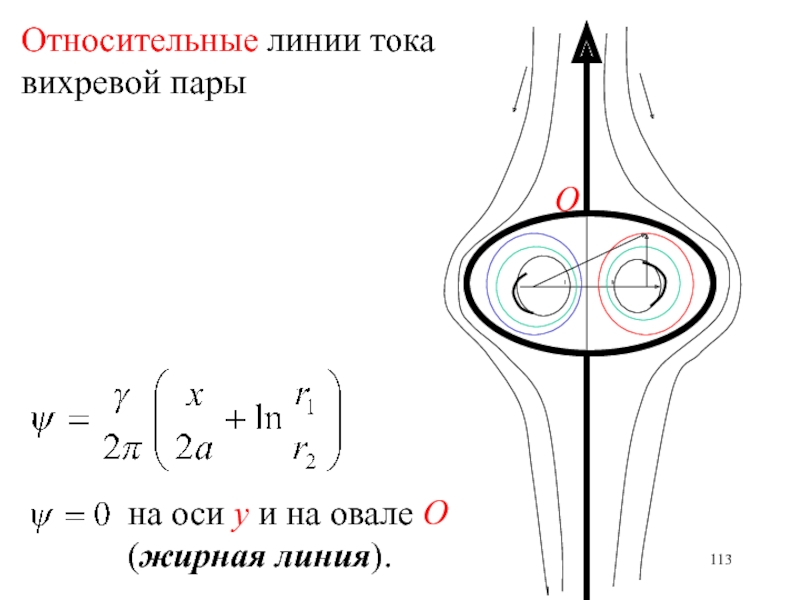
- 113. Относительные линии тока вихревой парыОна оси у и на овале О (жирная линия).
- 114. Жидкость внутри овала О движется вместе с
- 115. Найти в ортогональной системе координат уравнения линий
- 116. На линии токаz2z1
- 117. =constЛинии тока вихревой парыАВ
- 118. №3
- 119. При обтекании цилиндра жидкостью, его поверхность должна
- 120. При обтекании цилиндра жидкостью, его поверхность должна
- 121. Слайд 121
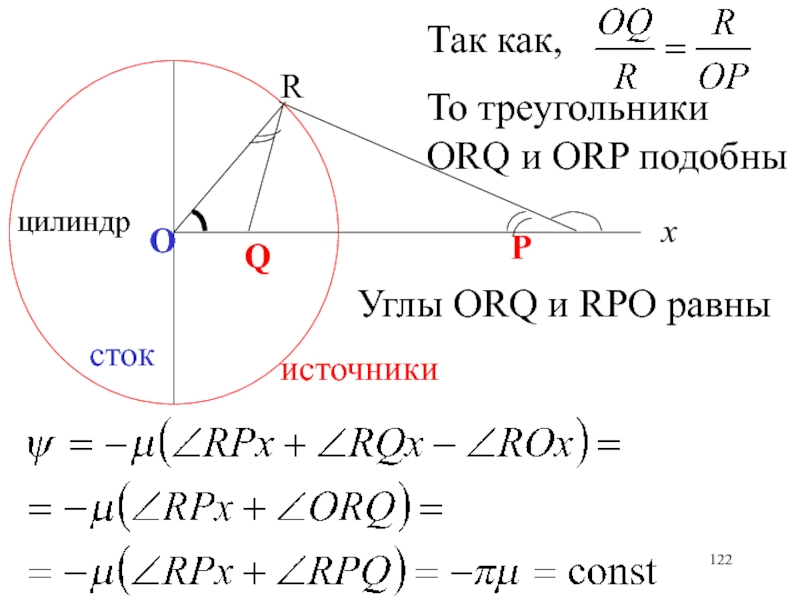
- 122. хцилиндрРОQRисточникистокТак как,То треугольники ORQ и ORP подобныУглы ORQ и RPO равны
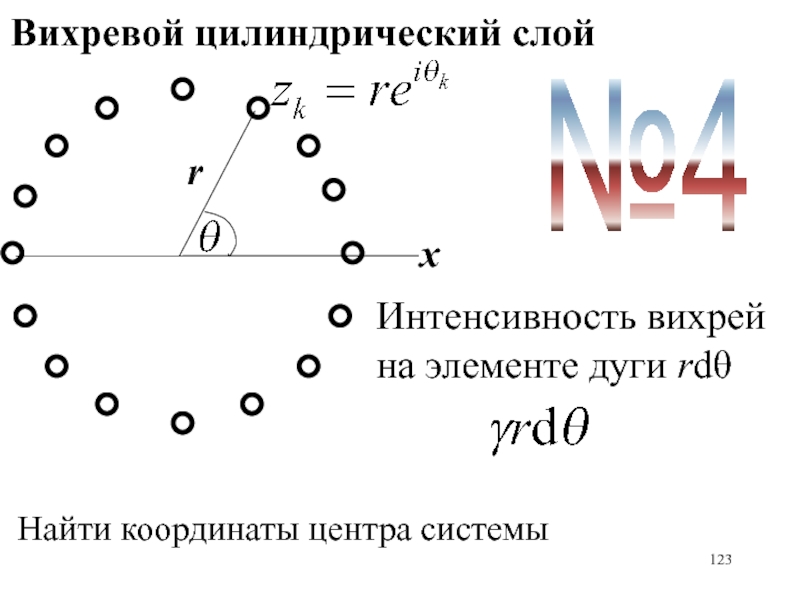
- 123. Вихревой цилиндрический слойxrИнтенсивность вихрей на элементе дуги rdНайти координаты центра системы№4
- 124. Интенсивность твердотельно вращающихся вихрей такова, что тангенциальные составляющие скорости в точках соприкосновения равныНайти координаты центра системы№5
- 125. РЕШЕНИЯ
- 126. UЗаписать функцию тока для вихревой пары в
- 127. Найти в ортогональной системе координат уравнения линий
- 128. №3
- 129. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Компоненты ротора скорости:
Вихревые линии - линии, направление которых совпадает всюду
с мгновенной осью вращения жидкости.
Слайд 4Дифференциальное уравнение вихревых линий
Если через каждую точку малой замкнутой кривой
провести соответствующую вихревую линию, то получим трубку, которая называется вихревой
трубкой. Жидкость внутри трубки образует вихревую нить или просто вихрь.Слайд 5 Задача
Заданы распределения вихря и дивергенции скорости в любой точке
жидкости, нормальная составляющая скорости на поверхности, ограничивающей данный объем жидкости
Слайд 6Предположения
Жидкость заполняет все пространство,
находится в покое на бесконечности.
Заданы вихрь
скорости Ω расхождение (дивергенция) скорости , равные 0 вне объема
.Область может быть разложена на конечное число частей, в которых и Ω равномерно непрерывны, так же как и их частные производные.
Слайд 75. На поверхностях разрыва нормальная составляющая Ω остается непрерывной
Искомую скорость
u будем рассматривать как сумму двух слагаемых: одно определяется расхождением
скорости, и ее вихрь равен нулю, а второе – ротором скорости, а ее дивергенция равна нулю.Слайд 9Для определения u1 получаем уравнение Пуассона
Предположим, что функция Θ равна
0 всюду, кроме очень малой окрестности τ0 начала координат, причем
Слайд 10По теореме Гаусса
Т.е. объемный интеграл от расхождения вектора скорости равен
потоку вектора скорости через поверхность S0, ограничивающую объем τ0. Поток
должен равняться единице в силу предположенияСлайд 11Пусть τ→0. Получаем картину течения от точечного источника в начале
координат интенсивности 1. В силу симметрии потенциал скорости φ –
функция только rφ всюду, кроме начала координат, удовлетворяет уравнению Лапласа
Слайд 12φ – функция только r, в сферических координатах нет зависимости
от широты и долготы.
Интегрируем:
Слайд 13Произвольная постоянная определяется из условия, что поток скорости через произвольную
сферу с центром в начале координат равен 1. На сфере
нормальная составляющая скорости имеет постоянное значение:а площадь поверхности сферы равна 4πr2
Слайд 14Получаем:
Произвольная постоянная не влияет на величину скорости течения и может
быть отброшена
Слайд 16Если задано распределение источников Θ(ξ, η, ζ)
Где r расстояние от
точки N(x,y,z), где ищем поле скорости до точки М(ξ,η,ζ), где
расположен источник. Интегрировать надо по (ξ,η,ζ).Слайд 18Определим вектор u2 для системы
Удовлетворим второму уравнению, если положим
где А
– векторный потенциал. Тогда
Можно доказать тождество:
Слайд 22Применяя к вихревой трубке свойство
учитывая, что боковые поверхности трубки –
есть вихревые линии, т.е. параллельны ротору скорости, получаем для суммарного
потока вихря:ds
Слайд 28Вклад в величину скорости в точке (x,y,z) от элемента вихревой
трубки ds определяется выражением:
Слайд 29Электродинамика:
Сила, действующая на магнитный полюс в точке (x,y,z) от элемента
проводника ds, по которому течет ток (Био и Савара)
Слайд 31Пусть движение происходит в плоскости х, у. Вихревые линии являются
прямыми, параллельными оси z. ξ, η, ζ – координаты точек
вихревой трубки, ds – элемент дуги трубкиСлайд 32Скорость жидкости в точке (х, у) определяется:
Считая ξ, η, (х,
у, z) постоянными, интегрируем
Слайд 33Достаточно рассматривать движение на плоскости 0xy, причем вместо вихревой нити
точку пересечения ее с плоскостью 0xy. Будем называть ее точечным
вихрем. Под влиянием такого вихря частицы жидкости двигаются по окружностям, центром которых является вихрь. Положительным соответствует движение против часовой стрелки.Вследствие симметрии движения центр вихря не будет смещаться.
Слайд 36 2 вихря
Две параллельные прямые вихревые нити в точках z1
и z2. Показать, что нити всегда сохраняют одинаковое расстояние друг
от друга и вращаются с постоянной угловой скоростью вокруг общего центра С. Пусть циркуляция одной нити равна 1 , а второй 2 .r
Запишите комплексный потенциал для 2 нитей.
Слайд 38Скорость первого вихря в точке z1 (сам на себя не
действует)
Скорость второго вихря в точке z2
Отделяем мнимые и действительные части.
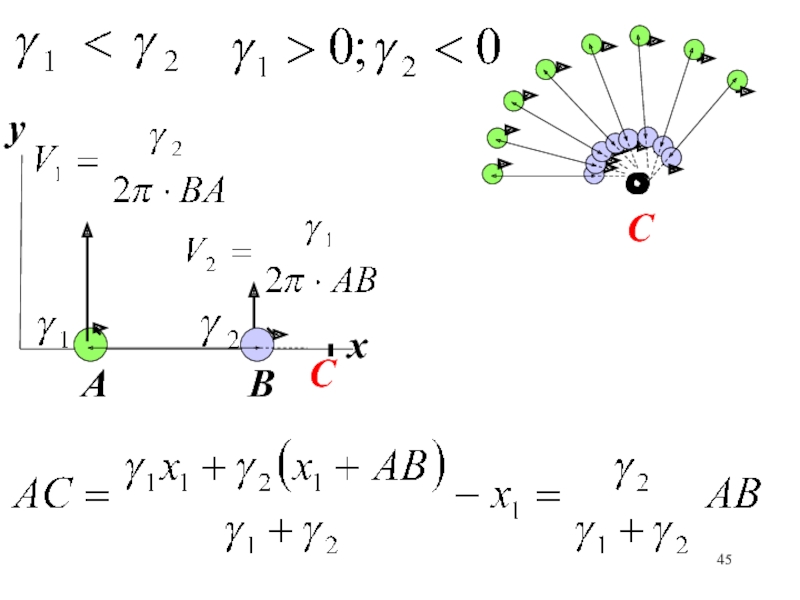
Обозначим расстояние между вихрямиСлайд 40Получаем интеграл движения центра инерции системы двух вихрей
Точка С (центр
инерции) с координатами
Остается неподвижной во все время движения
Слайд 43A
B
x
С
Два вихря, вращающиеся в разных направлениях, находятся в начальный момент
времени на вещественной оси.
Найти скорости вихрей, расстояние до центра
системы, угловую скорость вращения вихрей.Слайд 44Вихревая нить с координатами
и циркуляцией сообщает жидкости в точке
(х, у) скорость, компоненты которой равных
(х, у)
r
Слайд 46Угловая скорость вращения вихрей вокруг центра С
Где будет точка С,
если вихри вращаются в одном направлении?
Слайд 47x
r
Два вихря, вращающиеся в разных направлениях, находятся в начальный момент
времени на вещественной оси.
Найти скорости вихрей, расстояние до центра
системы.Слайд 48Скорость первого вихря в точке z1 (сам на себя не
действует)
Скорость второго вихря в точке z2
Отделяем мнимые и действительные части.
Обозначим расстояние между вихрямиСлайд 49Отделяем вещественную часть от мнимой :
Вихри перемещаются с постоянной скоростью,
перпендикулярно прямой, соединяющей вихри в положительном направлении оси у
Слайд 50Пример 1
Одна вихревая нить в точке (х,у), циркуляция скорости внутри
бесконечно малого сечения имеет постоянное значение.
Найти центр системы
Слайд 52Пример 2
Внутри круга радиуса а жидкость вращается как твердое тело
с угловой скоростью . Определить скорость вне круга.
Слайд 54Как будут двигаться 2 вихря радиуса а, если они имеют
циркуляцию разного знака, но одинаковую по модулю? Вихри вращаются как
твердое тело.Пример 3
А
а
В
а
А
В
Слайд 55Движение двух вихрей с противоположным направлением вращения и
С
А
АС=
V1=V2=
Вихри двигаются по
прямой с одинаковой скоростью
а
В
Слайд 59Так как скорость жидкости во всех точках плоскости симметрии направлена
по касательной, то можно предположить, что эта плоскость образует твердую
границу для жидкости. Таким образом систему «вихрь у твердой границы» можно смоделировать системой, представляющей собой пару вихрей. Вихрь у твердой границы будет перемещаться с постоянной скоростьюа
2а
Слайд 60Пример 5
В точке с координатами х,у находится прямая вихревая нить.
Жидкость ограничена твердыми стенками, образующими прямой угол вдоль осей координат.
Найти траекторию вихря.Слайд 62Так как циркуляция скорости вихря постоянна, то течение стационарно. В
этом случае траектория вихря совпадает с линией тока, проходящей через
точку (x,y)Для того, чтобы описать влияние стенки, расположенной вдоль мнимой оси, поместим вихрь той же интенсивности, но с противоположным знаком циркуляции в точку (-x,y ) (отразим вихрь)
Слайд 64Для того, чтобы описать влияние стенки, расположенной вдоль действительной оси,
поместим вихри той же интенсивности, но с противоположными знаками циркуляции
в точки (-x,-y ) и (x,-y )Слайд 78расположенных в точках z1,…, zn и имеющих интенсивности 1, …,
n
Комплексный потенциал
Комплексная скорость
Записать скорость вихря в точке zp (k=p)
n
вихрейСлайд 79Уравнение движения вихря в точке zp (k=p)
Умножая на p и
суммируя по переменной p от 1 до n, получаем в
правой частиТак как слагаемому с (zp-zk) соответствует слагаемое с (zk-zp)
Слайд 82Следствие 2
Уравнение движения вихря в точке zp (k=p)
Умножая на p zp и суммируя по переменной p от 1 до n, получаем
Отделить мнимую и действительную части
Слайд 83Сумма моментов количеств движения масс p относительно начала координат не
меняется со временем
(1)
(2)
(2)
Слайд 86Умножая выражения скорости на
и суммируя по переменной p от 1
до n, получаем еще один интеграл
Следствие 3
Слайд 87А
а
В
Такие вихри называются «парой вихрей». Они являются плоской аналогией вихревому
кольцу и обладает многими свойствами последнего.
Слайд 90Координаты точки М на вихревой нити в декартовой системе (x,
y, z)
Расстояние от точки М на вихревой нити до точки
N(x,y,z)Слайд 97ОПРЕДЕЛИТЬ объем жидкости, протекающей через круг с радиусом ρ, лежащий
в плоскости перпендикулярной оси z с центром на оси z
, через переменную АСлайд 98Объем жидкости, протекающей через круг с радиусом ρ, лежащим в
плоскости перпендикулярной оси z с центром на оси z
Слайд 103Вихревой цилиндрический слой
x
r
Интенсивность вихрей на элементе дуги rd
Записать комплексный потенциал
и комплексную скорость для точки z
Слайд 104Комплексный потенциал цилиндрического слоя в точке z
Комплексная скорость
Делим подинтегральное выражение
на z, умножаем на
Слайд 106Если z внутри окружности, т.е.
При изменении от 0 до
2 аргумент разности
меняется на 2, так как вектор обходит начало координат. Тогдаz
r
0
Слайд 107Если z вне окружности, т.е.
При изменении от 0 до
2 конец вектора
обходит замкнутый путь не содержащий начала координат. Тогдаz
r
0
Записать комплексную скорость внутри и вне цилиндра
Слайд 108Комплексная скорость
движения нет внутри цилиндра
вне цилиндра движение описывается воздействием вихревой
нити интенсивности 2r, расположенной в начале координат
Слайд 110U
Записать функцию тока для вихревой пары в потоке жидкости, имеющего
постоянную скоростью U. Скорость потока равна по модулю скорости пары,
но противоположна по направлению.№1
Слайд 114Жидкость внутри овала О движется вместе с вихрями.
Жидкость вне
овала О обтекает этот овал как твердый цилиндр.
Полуоси овала О
приблизительно имеют длину 2.09а и 1.73а.Слайд 115Найти в ортогональной системе координат уравнения линий тока для
1)
случая двух вихрей одинаковой интенсивности
2) пары вихрей
№2
Слайд 119При обтекании цилиндра жидкостью, его поверхность должна быть линией тока,
а =const.
Пусть в центре цилиндра имеется сток, а на
оси 0х лежат два источника: один внутри цилиндра, другой вне цилиндра, Q – инверсия точки Р, мощность одинакова. Показать, чтох
Р
О
Q
R
источники
сток
поверхность цилиндра является линией тока
Слайд 120При обтекании цилиндра жидкостью, его поверхность должна быть линией тока,
а =const.
Пусть в центре цилиндра имеется сток, а на
оси 0х лежат два источника: один внутри цилиндра, другой вне цилиндра, Q – инверсия точки Р, мощность одинакова. Показать, чтох
Р
О
Q
R
источники
сток
поверхность цилиндра является линией тока
Слайд 123Вихревой цилиндрический слой
x
r
Интенсивность вихрей на элементе дуги rd
Найти координаты центра
системы
№4
Слайд 124Интенсивность твердотельно вращающихся вихрей такова, что тангенциальные составляющие скорости в
точках соприкосновения равны
Найти координаты центра системы
№5
Слайд 126U
Записать функцию тока для вихревой пары в потоке жидкости, имеющего
постоянную скоростью U. Скорость потока равна по модулю скорости пары,
но противоположна по направлению.№1