1 Геометричні методи мінімізації булевих функцій Лекція 7 Геометричні методи

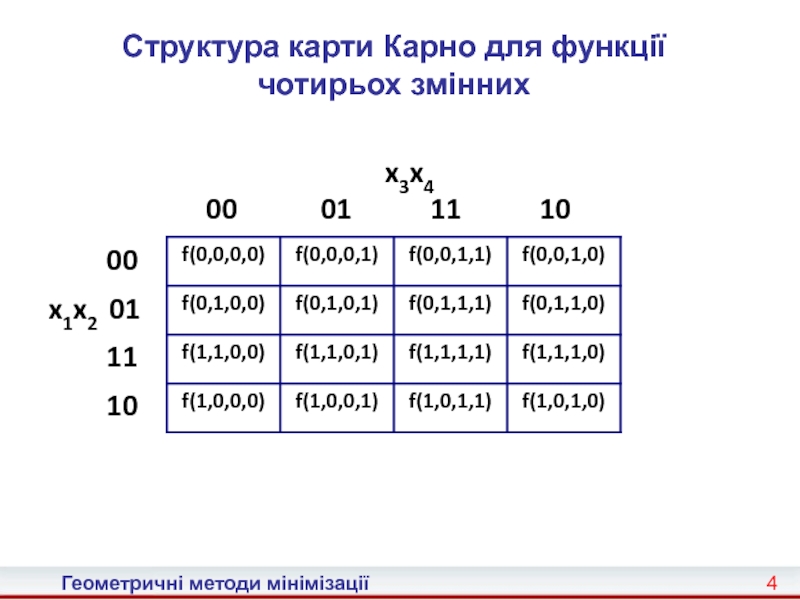
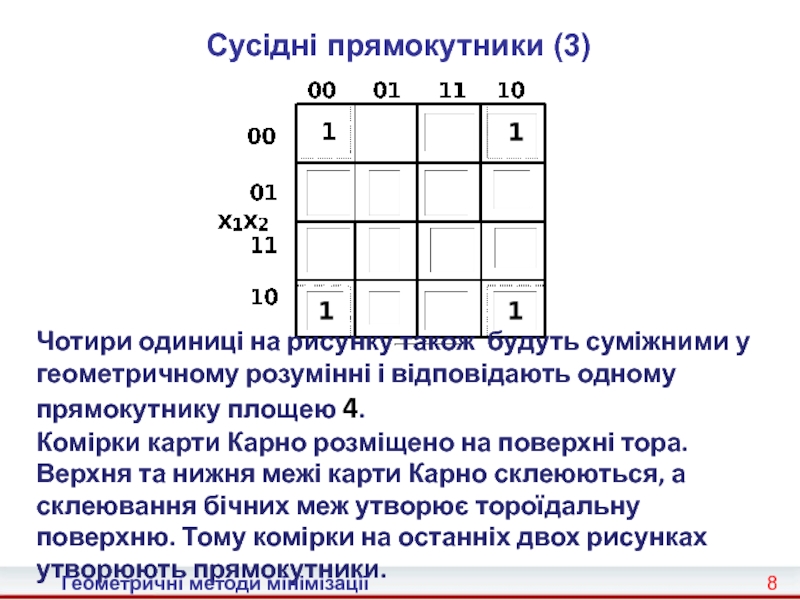
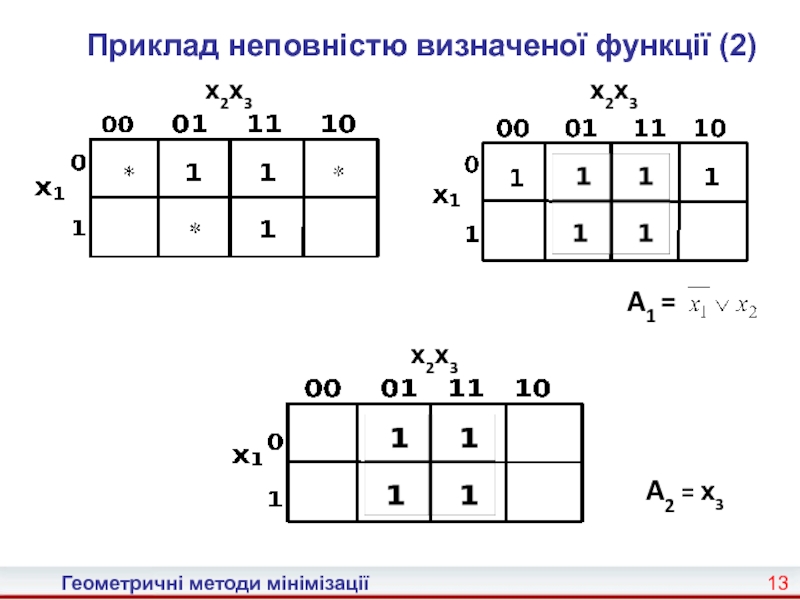
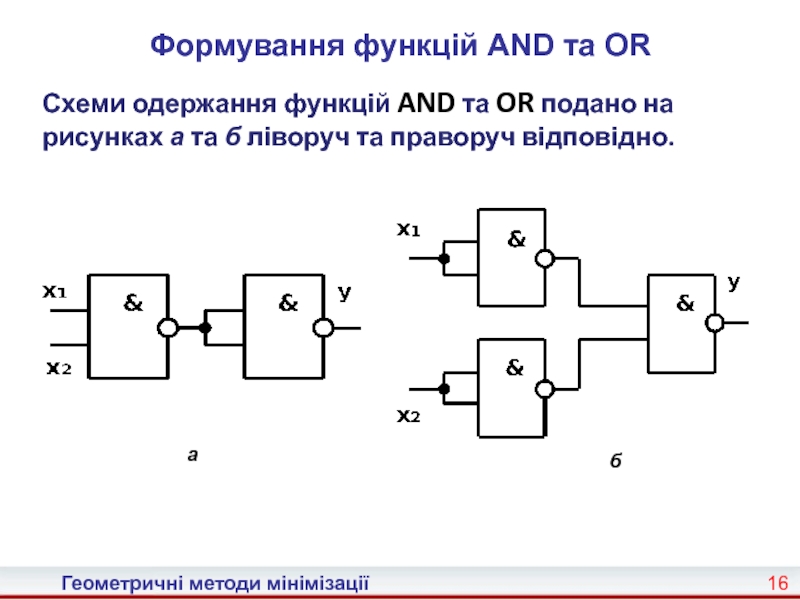
Карно, що є графічним представленням таблиць істинності булевих функцій. Таблиці

містять по 2n прямокутні комірки, де n – кількість логічних змінних. Карта розмічається системою координат, яка відповідає значенням змінних. Комбінація цифр у позначенні кожного стовпчика показує, для яких значень змінних обчислюється функція, розташована в його клітинках. Якщо на наборі (1, ..., n) значення функції дорівнює 1, то її д.д.н.ф. містить елементарну
кон'юнкцію , яка набуває значення 1. Тому комірки карти Карно, що являють функцію, містять стільки 1, скільки елементарних кон'юнкцій міститься в її д.д.н.ф., причому, кожній 1 відповідає одна з елементарних кон'юнкцій.

Геометричні методи мінімізації

x2x3
00 01 11 10

x1 0
1

x1 0
1

x2
0 1

Геометричні методи мінімізації

01

11 10

00

x1x2 01

11

10

Геометричні методи мінімізації

стовпчиків у карті Карно слідують не у природному порядку зростання

двійкових кодів, а у порядку 00, 01, 11, 10. Модифікацію порядку слідування наборів зроблено для того, щоб сусідні набори (які відрізняються один від одного тільки цифрою одного розряду) були сусідніми у геометричному розумінні.

Геометричні методи мінімізації

двох змінних, а квадрату, що

складається з однієї комірки, – елементарна кон'юнкція Відповідна покриттю функція має вигляд
f(x1, x2, x3, x4) =

Cусідні прямокутники (1)

Геометричні методи мінімізації

.

у геометричному розумінні. Одиниці у першому та четвертому рядках також

сусідніми у геометричному розумінні.

Cусідні прямокутники (2)

Геометричні методи мінімізації

і відповідають одному прямокутнику площею 4.
Комірки карти Карно розміщено на

поверхні тора. Верхня та нижня межі карти Карно склеюються, а склеювання бічних меж утворює тороїдальну поверхню. Тому комірки на останніх двох рисунках утворюють прямокутники.

Cусідні прямокутники (3)

Геометричні методи мінімізації

2k комірки, заповнені одиницями (k – ціле число). У прямокутники

поєднуються сусідні комірки, що відповідають сусіднім елементарним кон'юнкціям. Сукупність прямокутників, що покривають усі 1, називається покриттям. Одна й та сама комірка може бути покрита двома чи кількома прямокутниками.
Зробимо висновки:
1. Формула, отримана у результаті мінімізації булевої функції за допомогою карт Карно, містить стільки елементарних кон'юнкцій, скільки прямокутників є у покритті.
2. Чим більше комірок у прямокутнику, тем менше змінних у відповідній їй елементарній кон'юнкції.

Процес мінімізації булевої функції

Геометричні методи мінімізації

бічних сторін.
2. Комірки таблиці, що відповідають наборам змінних, на яких

значення функції дорівнює 1, заповняються одиницями, інші – не заповнюються (або заповнюються 0).
3. Вибирається найкраще покриття таблиці правильними прямокутниками, яким вважається утворене мінімальною кількістю прямокутників; якщо ж таких варіантів кілька, то з них вибирається той, що дає максимальну сумарну площу прямокутників. Якість мінімізації оцінюється функціоналом, що називається коефіцієнтом покриття k = m/s, де m – загальна кількість прямокутників; s – їх сумарна площа.

Послідовність дій за мінімізації булевих функцій
за методом карт Карно

Геометричні методи мінімізації

змінних, то її значення на вказаних наборах не визначено, що

у таблиці істинності функції позначаються знаком *.
На карті Карно комірки, відповідні забороненим наборам змінних, також позначаються знаком *. За мінімізації неповністю визначеної функції її варто додатково визначити (невизначені значення комірок карти Карно довільно довизначити як 0 або 1).
Якщо булева функція має m заборонених наборів змінних, то може існувати 2m варіантів розв'язку задачі довизначення функції. Бажано вибрати варіант, за якого формула мінімізованої функції буде найпростішою (матиме відповідне значення функціонала LЛ(A), LК(A) або LЗ(A).

Геометричні методи мінімізації

визначеної булевої функції і два варіанти її покриття. Зіставлення рис.

2.8 б і в дає змогу зробити висновок, що д.н.ф. A2 є кращою за д.н.ф. A1.

Приклад неповністю визначеної функції (1)

Геометричні методи мінімізації

х2х3

х2х3

A1 =

A2 = х3

Приклад неповністю визначеної функції (2)

Геометричні методи мінімізації

булеві функції. Якщо виходи одних елементів поєднати із входами інших,

то одержимо схему, що реалізує складніші функції. Сукупність різних типів елементів, достатніх для відтворення будь-якої булевої функції, називатимемо логічним базисом. Вище було показано, що елементи AND і NOT є таким логічним базисом, де елемент типу OR може бути отримано із елементів AND і NOT відповідно до рівняння Y =

Геометричні методи мінімізації

.

AND-NOT (булева функція штрих Шеффера).
Елемент AND-NOT
Геометричні методи мінімізації

та б ліворуч та праворуч відповідно.
Формування функцій AND та OR
б
а
Геометричні

методи мінімізації

логічними. Якщо у логічній схемі відсутні зворотні зв'язки, то їх

називають комбінаційними. Вони реалізують функції, значення яких на поточний момент часу визначаються тільки сукупністю значень вхідних змінних і не залежать від попередніх значень вхідних змінних. Комбінаційні схеми називають такими, що не мають властивості пам'яті (попередня історія не впливає на результат перетворення). За формального синтезу комбінаційних схем часом затримки логічних елементів нехтують.

Геометричні методи мінімізації

пристроєм, що виконує додавання двох однорозрядних чисел, є комбінаційний суматор.

Функції s (сума) і p (перенесення) для цього елемента подано у таблиці, а логічні рівняння подано нижче:

Схему однорозрядного комбінаційного суматора, що реалізовано у базисі AND-NOT, подано на наступному слайді (рис. а); на рис. б наведено його умовне позначення. Цей елемент інколи називають однорозрядним напівсуматором, оскільки у ньому не враховується можливість підсумовування ознак перенесення із попереднього розряду.

Геометричні методи мінімізації

наступному слайді (рис. а). Проміжна сума si' утворюється як результат

підсумування значень однойменних розрядів ai та bi вихідних чисел. Далі si підсумовується з ознакою перенесення pi-1 із попереднього розряду, утворюється остаточне значення суми si. Ознаки перенесення pi' і pi'' з обох напівсуматорів поєднуються за схемою OR, унаслідок чого виникає остаточне значення перенесення pi (обидві ознаки pi' і pi'' не можуть одночасно дорівнювати 1). Умовне позначення комбінаційного суматора на схемах подано на наступному слайді (рис. б).

Однорозрядний суматор

Геометричні методи мінімізації

слайд). На його виходах s1, ..., sn з'явиться код, відповідний

значенню суми двох n-розрядних вихідних двійкових чисел. Ознака pn використовується для індикації переповнення розрядної сітки комп'ютера.

n-розрядний комбінаційний суматор (1)

Геометричні методи мінімізації