1 Индуктивность По закону Био-Савара-Лапласа магнитная индукция пропорциональна

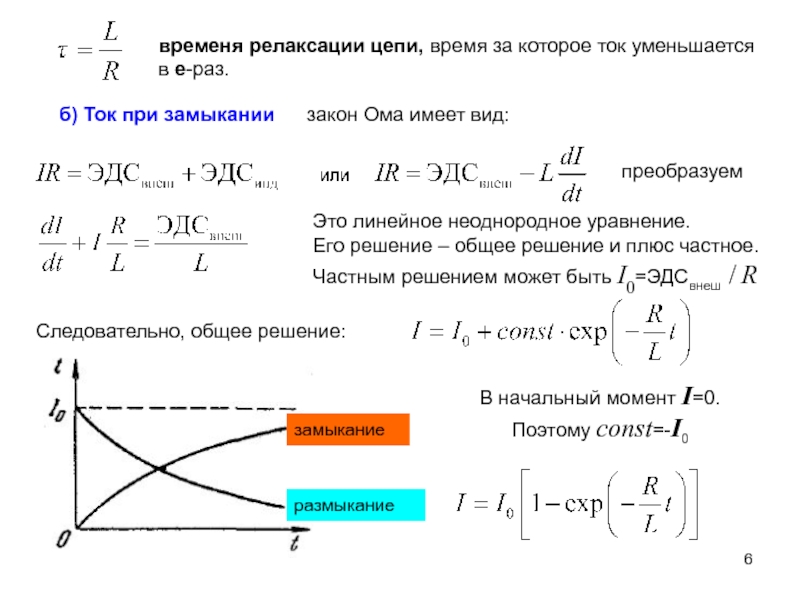
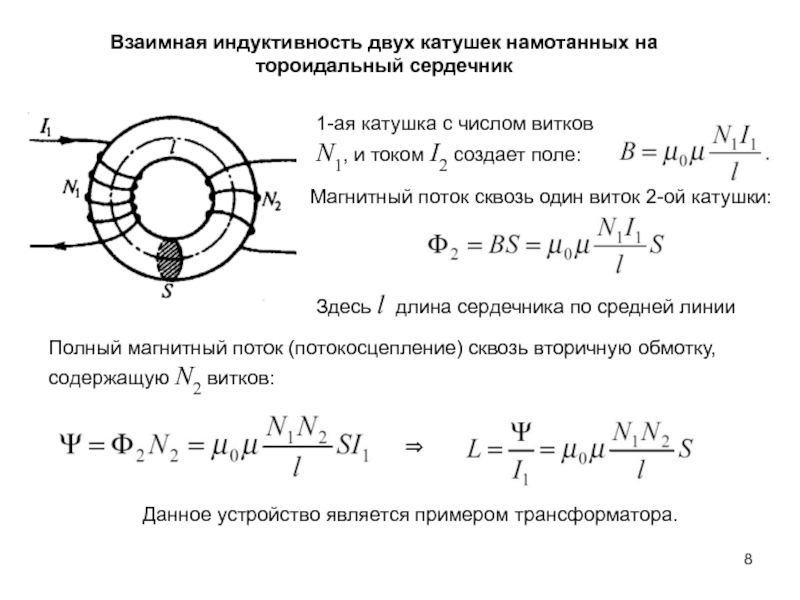
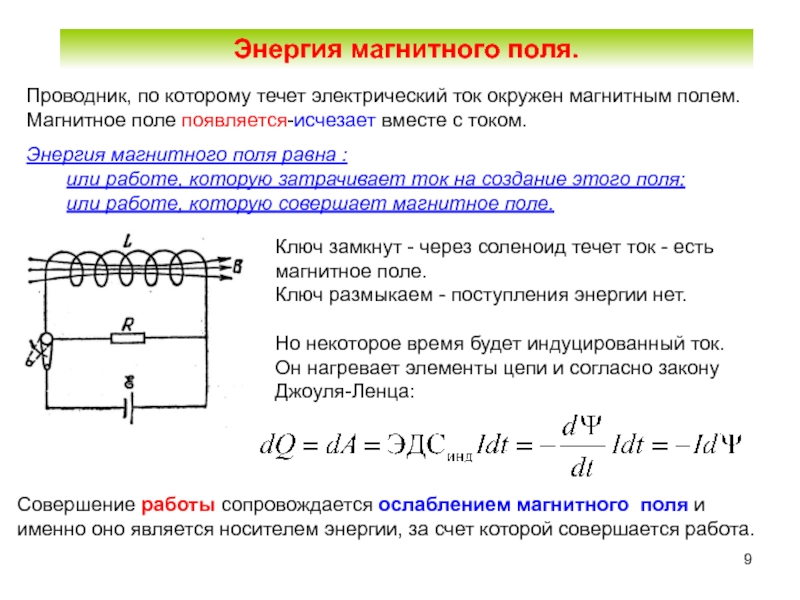
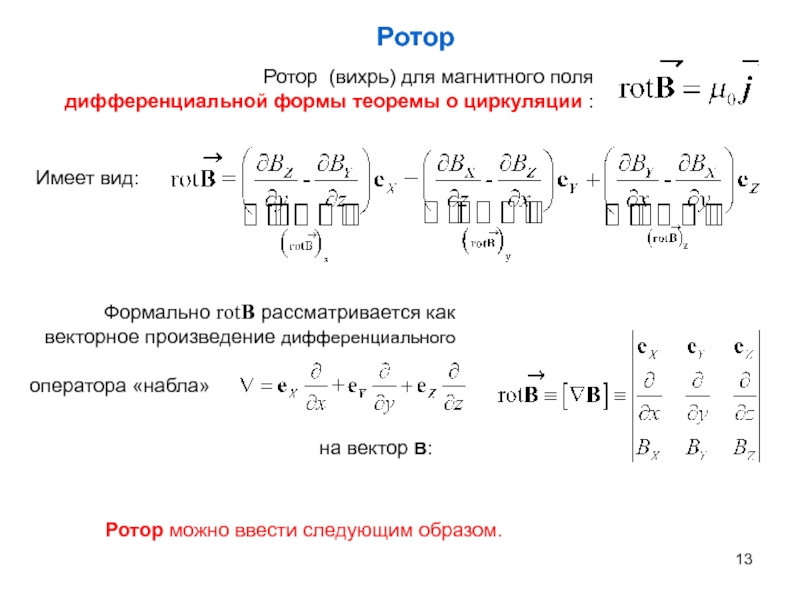
полного потока через контур можно записать:
Коэффициент пропорциональности – ИНДУКТИВНОСТЬ

Линейная зависимость имеет место если магнитная проницаемость среды, которой окружен контур, не зависит от напряженности поля Н,

т. е. в отсутствие ферромагнетиков, для них индуктивность является функцией тока

Поток

при отсутствии ферромагнетиков
– индуктивность величина постоянная
Единица индуктивности –

генри (Гн).
Это индуктивность контура, у которого при силе тока в 1 А в нем возникает магнитный поток в 1 Вб.

Индуктивность соленоида

Его магнитное поле:

Поток через каждый виток:

Полный поток сцепленный с соленоидом:

Следовательно

создаваемое током магнитное поле - меняется 
меняется и магнитный потока

через контур 
возникает ЭДС индукции

Вывод: изменение тока в контуре ведет к возникновению ЭДС индукции в самом контуре. Явление - самоиндукция.

ЭДС самоиндукции

Согласно закону Фарадея:

то:
Если контур находится в ферромагнитной среде, то:
« - » означает,

что ЭДС препятствует изменению силы тока.

Ток увеличивается - ЭДС препятствует увеличению
Ток уменьшается – ЭДС его поддерживает.

При явлениях самоиндукции ток обладает «инерцией» - стремятся сохранить магнитный поток неизменным.

замыкании-размыкании цепи ток в ней возникает или исчезает не мгновенно
а)

Ток при размыкании

В момент t=0 по цепи течет ток:

При размыкании ключа П возникает ток под действием ЭДСинд.
Закон Ома имеет вид:

Разделим переменные:

Общее решение:

сonst найдем из начальных условий.
При t=0 ток равен I0, следовательно,

где

б) Ток при замыкании
закон Ома имеет вид:
преобразуем
Это линейное неоднородное

уравнение.
Его решение – общее решение и плюс частное. Частным решением может быть I0=ЭДСвнеш / R

Следовательно, общее решение:

В начальный момент I=0.
Поэтому const=-I0

замыкание

размыкание

в одной электрической цепи при изменении электрического тока в другой

цепи или при изменении взаимного расположения этих двух цепей.

Ток текущий в контуре 1 создает связанный с контуром 2 магнитный поток :

Если сила тока изменяется, то возникает

Аналогично влияние и контура 2 на контур 1:

Коэффициенты L21 и L12 называются взаимной индуктивностью.
В отсутствии ферромагнетиков эти коэффициенты равны друг другу:

с числом витков N1, и током I2 создает поле:
Магнитный поток

сквозь один виток 2-ой катушки:

Здесь l длина сердечника по средней линии

Полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую N2 витков:



Данное устройство является примером трансформатора.

магнитным полем.
Магнитное поле появляется-исчезает вместе с током.

Энергия магнитного

поля равна :
или работе, которую затрачивает ток на создание этого поля;
или работе, которую совершает магнитное поле.

Ключ замкнут - через соленоид течет ток - есть магнитное поле.
Ключ размыкаем - поступления энергии нет.

Но некоторое время будет индуцированный ток.
Он нагревает элементы цепи и согласно закону Джоуля-Ленца:

Совершение работы сопровождается ослаблением магнитного поля и именно оно является носителем энергии, за счет которой совершается работа.

в соленоиде:
Сцепленный с соленоидом поток:
V-объем соленоида
Подставим
Сама объемная плотность энергии

поля:

Приращение объемной плотности:

Если среда не ферромагнетик то:

силы тока и индуктивности, и не видно, что она относится

к соленоиду, поэтому эта формула справедлива для проводника любой формы.

В случае связанных контуров энергия магнитного поля определяется:

собственные энергии токов взаимная энергия токоа

и магнитного полей.
Дивергенция
Дивергенция (расхождение) для электростатического поля дифференциальная

форма теоремы Гаусса :

Характеризует распределение источников и стоков (здесь электрического поля, а общем может быть любого поля). Является скалярной величиной.

Математическое определение дивергенции:

Изменение потока при бесконечно малом изменении объема:

циркуляции :
Имеет вид:
Формально rotB рассматривается как векторное произведение дифференциального
на

вектор В:

оператора «набла»

Ротор можно ввести следующим образом.

и dz. Его плоскость  к оси X.
Вклад стороны

CD:

Сумма сторон АВ и CD:

Вклад стороны АВ:

Сумма сторон BC и DA:

Циркуляция по контуру ABCD:

В предельном случае ротор всегда перпендикулярен поверхности, поэтому

вектора rotA через произвольную поверхность S, ограниченную данным контуром.
Доказательство.
Для

элементарного контура ограничивающего элементарную площадку показано:

Просуммируем все элементарные площадки, составляющие рассматриваемую площадь S и элементарные циркуляции, которые охватывают эти элементарный площадки:

Правая сумма в пределе, при бесконечно малых площадках равна:

Именно это выражение и находится в правой части теоремы

ее вычисления поступим следующим образом.
Разобьем рассматриваемую площадь на две.

Это

все равно представляет правую часть теоремы.
Циркуляция охватывающая всю площадь будет состоять из двух циркуляций:

Циркуляция по этим двум площадям равна циркуляции по внешнему контуру. Аналогичный результат получается если разбить S на бесконечно малые dS, т.е.

равна циркуляции по внешнему контуру

или

В результате теорема доказана

в том числе и объемной.
и разбивая ее на бесконечно

малые участки всегда можно достичь нормали.

левой части применим теорему Стокса получим:
или
Контур L охватывает поверхность

S

Это электрическое поле может включать в себя как вихревое так и электростатическое, поскольку

и магнитное поля симметричны в своем взаимодействии:
меняющееся во времени магнитное

поле создает электрическое поле, меняющееся во времени электрическое поле (dE/dt) создает магнитное поле.

Из наличия магнитного поля - всегда следует наличие электрического тока, если даже мы его не видим.
Этим током является ток смещения

Его плотность

Величина

- плотность полного тока.

Сам полный ток:

виде :
Дифференциальная форма этого уравнения:
Как показало время (опыт) данное

выражение выполняется всегда

ток по замкнутой поверхности равен нулю.
На концах проводников обрывается

лишь ток проводимости, а в диэлектрике между концами проводника имеющийся ток смещения замыкает ток проводимости.

2) Ток смещения и ток проводимости эквивалентны в том, что создают магнитное поле. Это единственное физическое свойство тока смещения.

3) Ток смещения существует там, где меняется со временем электрическое поле. Всякое изменение во времени электрического поля создает ток смещения и тем самым возбуждает в окружающем пространстве магнитное поле.

4) В диэлектриках ток смещения состоит из двух существенно различных слагаемых:

Открытие Максвеллом тока смещения - теоретическое открытие.

полей: E и В
Вторая пара уравнений содержит дополнительные характеристики полей:

D и H

замкнутому контуру равна со знаком минус производной по времени от

магнитного потока через любую поверхность, ограниченную данным контуром.

Поток вектора D сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.

Циркуляция вектора Н по любому замкнутому контуру равна полному току (ток проводимости + ток смещения) через произвольную поверхность, ограниченную данным контуром.

4. Поток вектора В сквозь произвольную замкнутую поверхность всегда равен нулю.

Содержание уравнений Максвелла в интегральной форме.

Для стационарных полей уравнения Максвелла распадаются на две пары независимых уравнений:
стационарного электрического поля и стационарного магнитного поля

и токов
интегральная и дифференциальная формы эквивалентны.
При разрывах (где

свойства среды или полей меняются скачкообразно) интегральная форма уравнений является более общей.

Первое и последнее справедливы если нет свободных зарядов и токов проводимости.

Дифференциальная форме уравнений Максвелла в этих областях должны быть дополнены граничными условиями:

Дифференциальные уравнения с уравнением движения заряженных частиц:

составляют фундаментальную систему уравнений, достаточную для описания всех электромагнитных явлений без квантовых эффектов.

решения этой задачи независимо от среды эти уравнения необходимо дополнить

уравнениями, включающими индивидуальные свойства среды
Это материальные уравнения. Для наиболее простых случаев:
слабых электромагнитных полей;
медленно меняющихся в пространстве и во времени;
изотропных сред;
отсутствие сегнетоэлектриков и ферромагнетиков;
материальные уравнения имеют вид:

где 0, 0 - электрическая и магнитная постоянные; ,  - диэлектрическая и магнитная проницаемости;  - удельная проводимость вещества.

из объема через замкнутую поверхность, равен убыли зарядов в единицу

времени внутри этого объема.

3) Выполняются во всех инерциальных системах отсчета.
Релятивистски инварианты. Вид уравнений не меняется, но входящие
в них величины преобразуются по определенным правилам.

4) Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что существует электрические заряды, но нет магнитных.

Линии вихревого электрического поля, индуцированного изменением В, образуют с вектором дB/dt левовинтовую систему.
Линии магнитного поля, индуцируемого изменением D, образуют с вектором dD/dt правовинтовую систему.

либо изменяющиеся во времени магнитные поля.
магнитные поля могут возбуждаться

либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.
переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле.
электромагнитное поле способно существовать самостоятельно – без электрических зарядов и токов.

Если последнее реализуется, то изменения электромагнитного поля имеют волновой характер.

Эти поля называются электромагнитными волнами.

или электромагнитное возмущение произвольной формы) характеризуется следующими общими свойствами:
1) скорость

в непроводящей нейтральной неферромагнитной среде:

2) векторы E, B,  (скорость волны) взаимно перпендикулярны и образуют правовинтовую систему. Это внутреннее свойство не зависящее от системы координат

3) Векторы E и B всегда колеблются в одинаковых фазах.

Между мгновенными значениями E и B в любой
точке существует соотношение

«Мгновенная фотография» электромагнитной волны

электрического и магнитного поля имеется энергия, то и электромагнитное поле

ее обладает. Убыль энергии означает, что из какой-то области энергия вытекает за ее границы. Поэтому, есть некий вектор П, характеризующий плотность потока энергии и можно записать:

Теорема Пойтинга: убыль энергии за единицу времени в данном объеме равна потоку энергии сквозь поверхность, ограниченную этим объемом, плюс мощность Р, которую силы поля производят над зарядами вещества внутри данного объема.

Плотность энергии электромагнитной волны- сумма электрического и магнитного полей:

векторная величина представляет плотность потока энергии электромагнитного поля и называется вектором Пойтинга