Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Растровая графика URL: http://www.school30.spb.ru/cgsg/cgc/ E-mail:
Содержание
- 1. 1 Растровая графика URL: http://www.school30.spb.ru/cgsg/cgc/ E-mail:
- 2. ПримитивыТочкиЛинииПрямоугольники (со сторонами, параллельными границам экрана)МногоугольникиШрифтыЗаливка областейПлоское отсечение
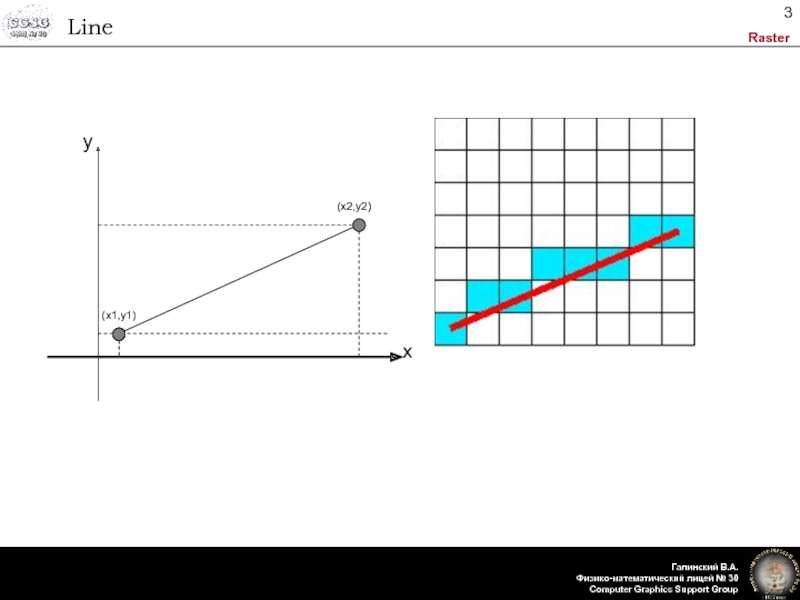
- 3. Line
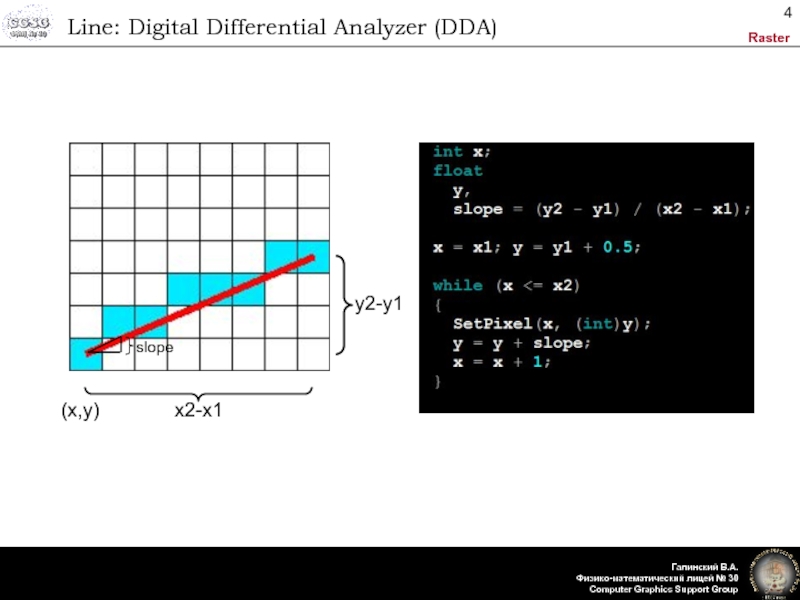
- 4. Line: Digital Differential Analyzer (DDA)(x,y)x2-x1y2-y1slope
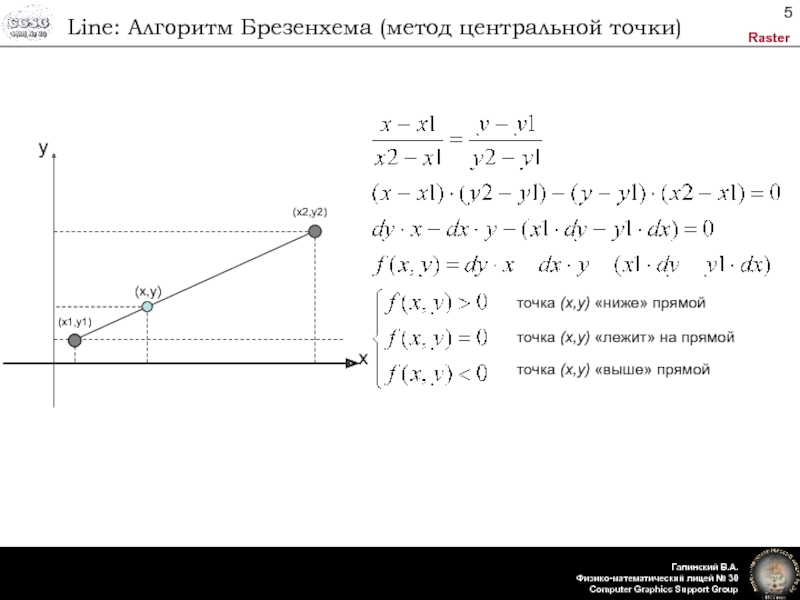
- 5. Line: Алгоритм Брезенхема (метод центральной точки)точка (x,y) «ниже» прямойточка (x,y) «лежит» на прямойточка (x,y) «выше» прямой
- 6. Line: Алгоритм Брезенхема (метод центральной точки)P(x,y)M(x+1,y+1/2)f(x,y)Подставляем точку
- 7. Line: Алгоритм Брезенхема (метод центральной точки)P(x,y)ME(x+2,y+1/2)f(x,y)Подставляем точку
- 8. Line: Алгоритм Брезенхема (метод центральной точки)P1(x1,y1)M0(x+1,y+1/2)f(x,y)Известны приращения f.Найдем первоначальное значение для точки (x1,y1)
- 9. Line: Алгоритм Брезенхема (метод центральной точки)Сохранились вещественные
- 10. Line: Алгоритм Брезенхема (метод центральной точки)
- 11. Line: Алгоритм с использованием Fixed Point (DDA)Fixed
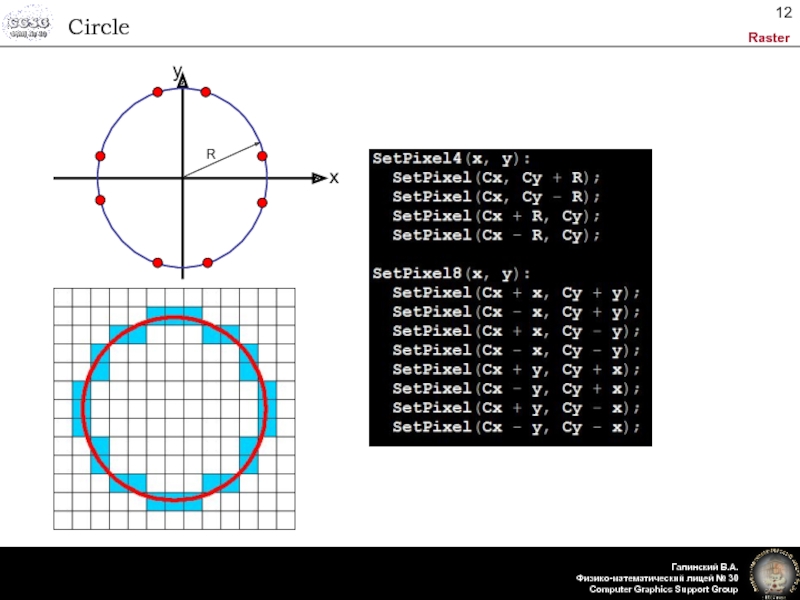
- 12. CircleR
- 13. Circle: Алгоритм Брезенхема (метод центральной точки)Подставляем точку
- 14. Circle: Алгоритм Брезенхема (метод центральной точки)P(x,y)MESEMSEMEf(x,y)Изменения значения f(M) при переходек новым точкам (E или SE):
- 15. Circle: Алгоритм Брезенхема (метод центральной точки)Определили приращения
- 16. Circle: Алгоритм Брезенхема (метод центральной точки)Дополнительная оптимизация:Просчитаем
- 17. Circle: Алгоритм Брезенхема (метод центральной точки)
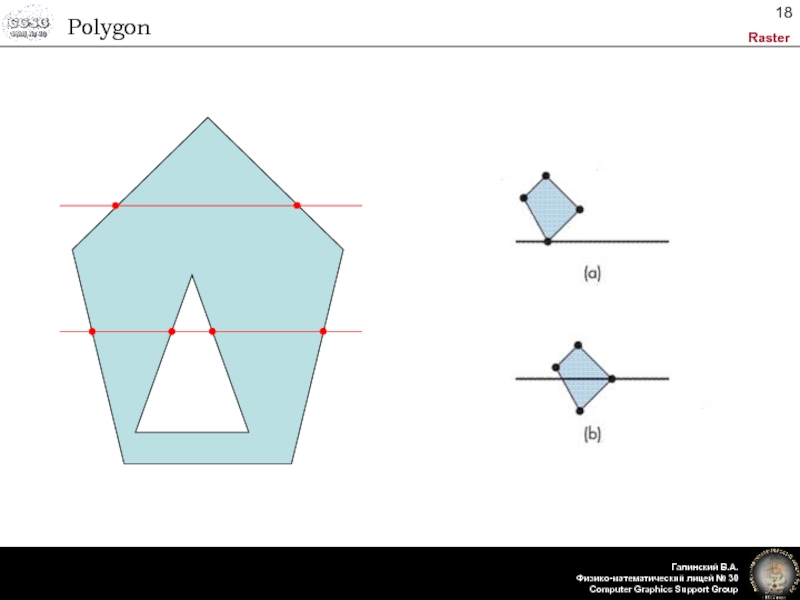
- 18. Polygon
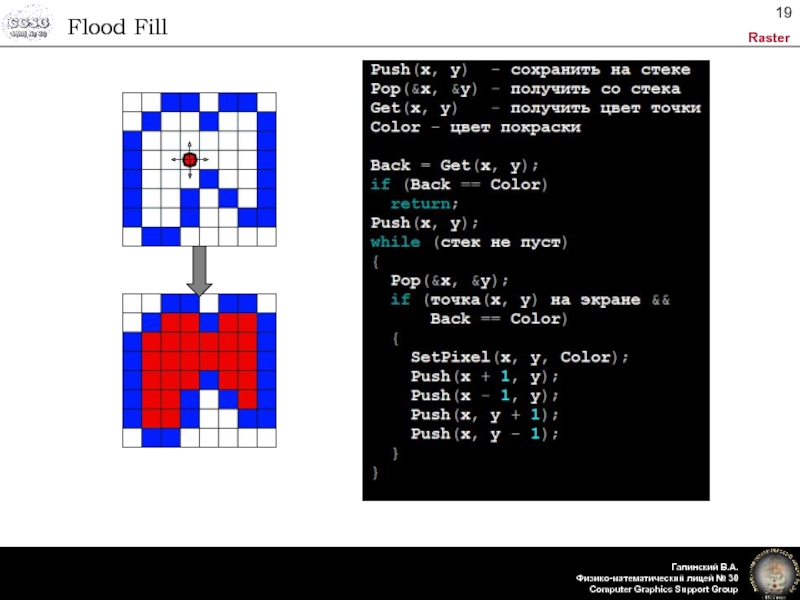
- 19. Flood Fill
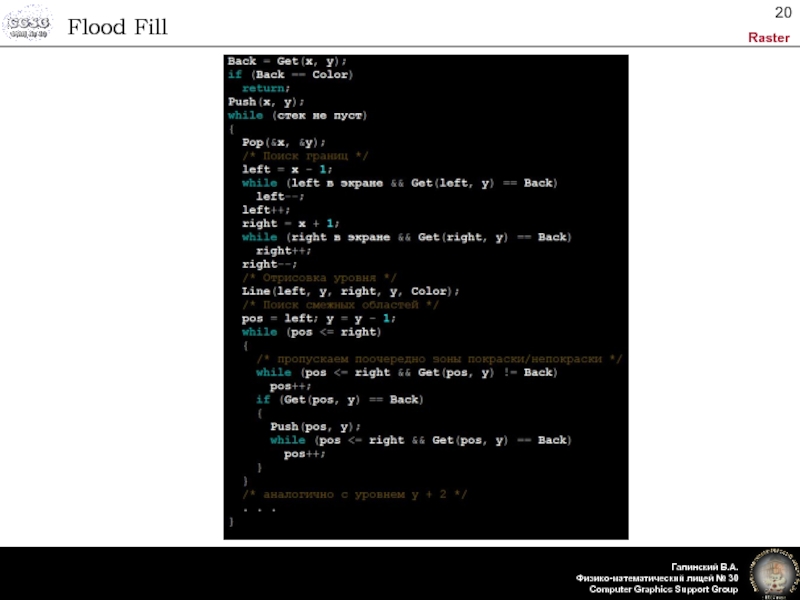
- 20. Flood Fill
- 21. TextШрифтыРастровые Векторные Контурные
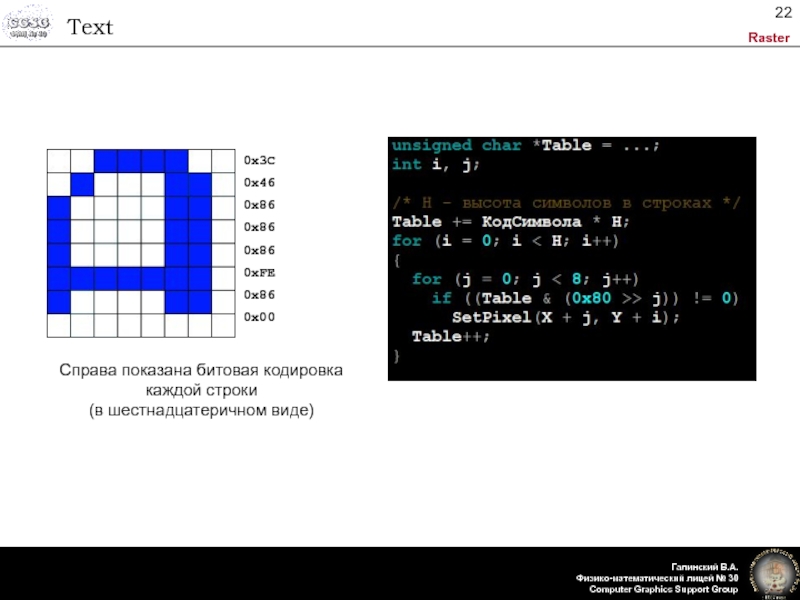
- 22. Text0x3C0x460x860x860x860xFE0x860x00Справа показана битовая кодировка каждой строки (в шестнадцатеричном виде)
- 23. УпражнениеРекомендуется реализовать растровые алгоритмы с помощью программы из первого упражнения. Растровые шрифты необходимо загружать из файла.
- 24. Скачать презентанцию
ПримитивыТочкиЛинииПрямоугольники (со сторонами, параллельными границам экрана)МногоугольникиШрифтыЗаливка областейПлоское отсечение
Слайды и текст этой презентации
Слайд 2Примитивы
Точки
Линии
Прямоугольники (со сторонами, параллельными границам экрана)
Многоугольники
Шрифты
Заливка областей
Плоское отсечение
Слайд 5Line: Алгоритм Брезенхема (метод центральной точки)
точка (x,y) «ниже» прямой
точка (x,y)
«лежит» на прямой
Слайд 6Line: Алгоритм Брезенхема (метод центральной точки)
P(x,y)
M(x+1,y+1/2)
f(x,y)
Подставляем точку M в функцию
f:
если f(M) > 0 выбираем точку NЕ
если f(M)
выбираем точку ЕE
NE
Слайд 7Line: Алгоритм Брезенхема (метод центральной точки)
P(x,y)
ME(x+2,y+1/2)
f(x,y)
Подставляем точку M в функцию
f:
если f(M) > 0 выбираем точку NЕ
если f(M)
выбираем точку ЕИзменения значения f(M) при переходе
к новым точкам (E или NE):
E
NE
MNE(x+2,y+3/2)
M
Слайд 8Line: Алгоритм Брезенхема (метод центральной точки)
P1(x1,y1)
M0(x+1,y+1/2)
f(x,y)
Известны приращения f.
Найдем первоначальное значение
для точки (x1,y1)
Слайд 9Line: Алгоритм Брезенхема (метод центральной точки)
Сохранились вещественные числа.
Сделаем замену: 2f
= e
Тогда помеченные строки изменяться на:
e = 2 * dy
- dx;e > 0
e = e + 2 * dy - 2 *dx;
e = e + 2 * dy
и e – целое число.
Слайд 11Line: Алгоритм с использованием Fixed Point (DDA)
Fixed Point – вещественные
числа с фиксированной точкой.
Рассмотрим 4-байтное целое:
2b целая часть
2b дробная часть
Точность
1/65536Если x и y fixed point, то
сложение не изменяется (x+y)
вычитание не изменяется (x-y)
целая часть – «двоичный сдвиг» вправо на 16 бит (x >> 16)
из целого: x = a << 16
Слайд 13Circle: Алгоритм Брезенхема (метод центральной точки)
Подставляем точку M в функцию
f:
если f(M) >= 0 выбираем точку SЕ
если f(M) < 0
выбираем точку Е
Слайд 14Circle: Алгоритм Брезенхема (метод центральной точки)
P(x,y)
M
E
SE
MSE
ME
f(x,y)
Изменения значения f(M) при переходе
к
новым точкам (E или SE):
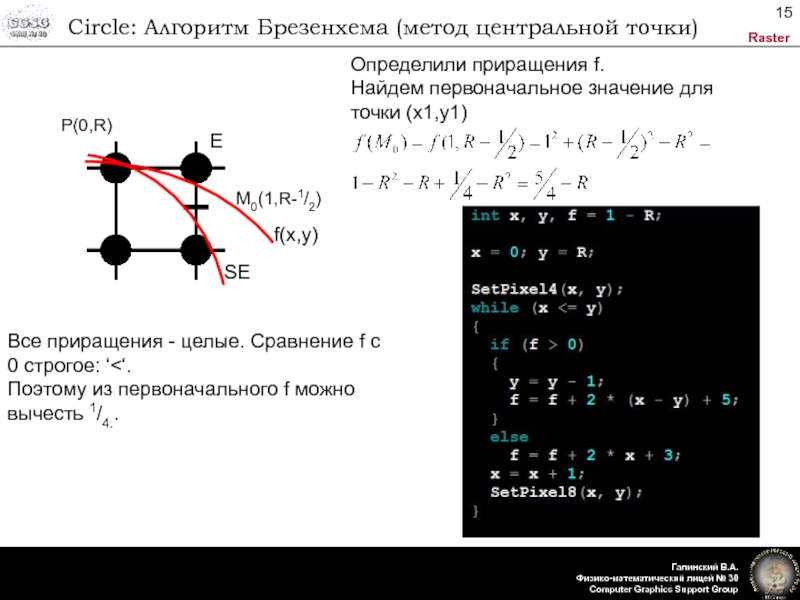
Слайд 15Circle: Алгоритм Брезенхема (метод центральной точки)
Определили приращения f.
Найдем первоначальное значение
для точки (x1,y1)
Все приращения - целые. Сравнение f с 0
строгое: ‘<‘.Поэтому из первоначального f можно вычесть 1/4..
Слайд 16Circle: Алгоритм Брезенхема (метод центральной точки)
Дополнительная оптимизация:
Просчитаем изменение приращений по
направлениям E и SE (incrE=2*x+3 и incrSE=2*(x-y)+5) для избавления от
доступа к переменным.Если выбрана точка E, то ‘x’ увеличивается на 1 и:
incrE=incrE+2 и incrSE=incrSE+2
Если выбрана точка SE, то ‘x’ увеличивается на 1, ‘y’ уменьшается на 1 и:
incrE=incrE+2 и incrSE=incrSE+4
Изначальные значения:
incrE=3 и incrSE=5-2*R
Слайд 22Text
0x3C
0x46
0x86
0x86
0x86
0xFE
0x86
0x00
Справа показана битовая кодировка каждой строки
(в шестнадцатеричном виде)
Слайд 23Упражнение
Рекомендуется реализовать растровые алгоритмы с помощью программы из первого упражнения.
Растровые шрифты необходимо загружать из файла.
![Автоматизация звука [р] в словах и фразах.](/img/thumbs/44fdd0dc72de37584f4448c687e4a2fa-800x.jpg)
