Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
1 Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних
Содержание
- 1. 1 Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних
- 2. 2Сіденко Володимир Павлович,Старший викладач кафедри “Безпека інформаційних
- 3. 3Лекція № 20АЛГОРИТМ АСИМЕТРИЧНОГО ШИФРУВАННЯ ДАНИХ RSA
- 4. 4Питання лекції № 20 1. Створення відкритого й
- 5. 51. СТВОРЕННЯ ВІДКРИТОГО Й СЕКРЕТНОГО КЛЮЧІВ ДЛЯ АЛГОРИТМУ RSA
- 6. 61.1. Історія створення алгоритму RSA Троє вчених Рональд
- 7. 7 Після роботи над більш ніж 40 мож
- 8. 8 В основу криптографічної системи з відкритим ключем
- 9. 9 Кожний учасник створює свої відкри тий і
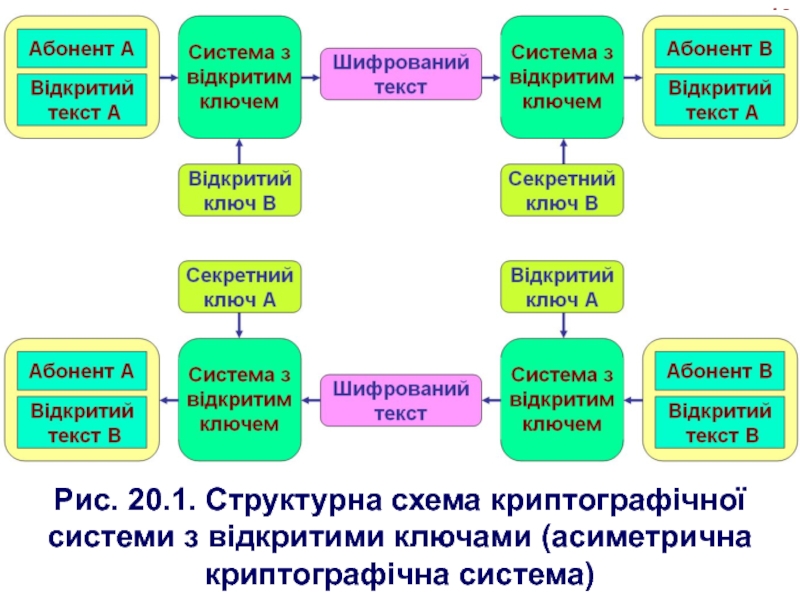
- 10. 10Рис. 20.1. Структурна схема криптографічної системи з відкритими ключами (асиметрична криптографічна система)
- 11. 11 Зашифрований текст у принципі не мо же
- 12. 121.2. Алгоритм створення ключів RSA 1. Кожний абонент
- 13. 13ми RSA. Звичайно в якості e беруть прості
- 14. 14 Як видно з виразу (20.2) відкритий та
- 15. 15 Крипостійкість алгоритму RSA при ата кі на
- 16. 16ВИСНОВКИ В основу криптографічної системи з відкритим ключем
- 17. 172. ЗАШИФРУВАННЯ Й РОЗШИФРУВАННЯ ПОВІДОМЛЕНЬ ЗА ДОПОМОГОЮ АЛГОРИТМУ RSA
- 18. 182.1. Алгоритм зашифрування йрозшифрування повідомленьза допомогою RSA Нехай
- 19. 19 Помітимо, що відповідно до (20.3) DK∙(C) =
- 20. 20 Якщо НСД (М, p) = р, то
- 21. 21 Аналогічно можна показати, що
- 22. 22 Оскільки р і q - різні прості
- 23. 23Алгоритм зашифрування повідомленнявід A до B 1. Вибрати
- 24. 24Алгоритм розшифрування повідомлення від A до B 1.
- 25. 252.2. Приклад використання алгоритму RSA для зашифрування й розшифруванняповідомлень
- 26. 26 Для обміну повідомленнями абоненти системи створюють ключі. Нехай
- 27. 27 Для знаходження секретного ключа dB абоненту B
- 28. 28 Оскільки -137 mod 480 = 343, то
- 29. 29 Представимо дане повідомлення у виг ляді послідовності
- 30. 30 Укладаючись у заданий інтервал 0,…,526, одержуємо наступне
- 31. 31 У підсумку одержуємо зашифровані да ні:
- 32. 32 При розшифруванні абоненту B потрібно виконати наступну
- 33. 33474 4 mod 527 = 237;
- 34. 34 Аналогічно407 343 mod 527 = 33,тобто
- 35. 35ВИСНОВКИ Шифрування та розшифрування даних криптографічним алгоритмом RSA
- 36. 363. КРИПТОСТІЙКІСТЬ АЛГОРИТМУ RSA
- 37. 37 Неважко показати, що складність зна ходження секретного
- 38. 38 2) числа р і q повинні бути
- 39. 39 У цей час самі більші прості числа,
- 40. 40 Знаючи одну із трьох величин: p, q
- 41. 41 Насправді, якщо в мережі викорис товується єдиний
- 42. 42 Більше того, це можна зробити навіть без
- 43. 43 Наприклад, вибравши е = 3 (при цьому
- 44. 44 Якщо експонента е вибирається випад ково, то
- 45. 45 Нехай, наприклад, три кореспонденти мають попарно взаємно
- 46. 46яке лежить в інтервалі 0 < y
- 47. 47ВИСНОВКИ Криптографічна стійкість алгоритмом RSA базується на складності
- 48. Скачать презентанцию
2Сіденко Володимир Павлович,Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”Тема № 8ПРИНЦИПИ ПОБУДОВИ АЛГОРИТМІВ АСИМЕТРИЧНОГО ШИФРУВАННЯ. АЛГОРИТМ RSA
Слайды и текст этой презентации
Слайд 11
Сіденко Володимир Павлович,
Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”
ЗМІСТОВНИЙ
МОДУЛЬ № 4
Слайд 22
Сіденко Володимир Павлович,
Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”
Тема
№ 8
ПРИНЦИПИ ПОБУДОВИ АЛГОРИТМІВ АСИМЕТРИЧНОГО ШИФРУВАННЯ. АЛГОРИТМ RSA
Слайд 44
Питання лекції № 20
1. Створення відкритого й секрет ного ключів
для алгоритму RSA
2. Зашифрування й розшифруван ня повідомлень за допомогою
алгорит му RSA3. Криптостійкість алгоритму RSA
Література: Л2, с. 310 – 318; Л3, с. 128 – 136.
Слайд 66
1.1. Історія створення алгоритму RSA
Троє вчених Рональд Райвест (Ronald Linn
Rivest), Ади Шамир (Adi Shamir) і Леонард Адлеман (Leonard Adleman)
з Масачусетського Технологічного Інституту (MIT) приступилися до пошуків математич ної функції, яка б дозволяла реалізувати сформульовану Уитфилдом Диффи і Мар тином Хеллманом модель криптографічної системи з відкритим ключем.
Слайд 77
Після роботи над більш ніж 40 мож ливими варіантами, їм
вдалося знайти ал горитм, заснований на відмінності в тому, наскільки
легко знаходити більші прості числа й наскільки складно розкладати на множники добуток двох більших простих чисел, що одержав згодом назву RSA.Система була названа по перших бук вах прізвищ її авторів.
Опис RSA було опубліковано в серпні 1977 року у журналі Scientific American.
Слайд 88
В основу криптографічної системи з відкритим ключем RSA покладена задача
множення й розкладання складених чисел на прості співмножники, яка є
обчислю вальне односпрямованою задачею (тест простоти, факторизація).У криптографічній системі з відкритим ключем кожний учасник створює як відкри тий ключ (public key), так і секретний ключ (secret key).
Кожний ключ - це частина інформації. У криптографічній системі RSA кожний ключ складається з пари цілих чисел.
Слайд 99
Кожний учасник створює свої відкри тий і секретний ключі самостійно.
Секретний
ключ кожний з них тримає в секреті, а відкриті ключі
можна повідом ляти кого завгодно або навіть публікувати їх.Відкритий і секретний ключі кожного учасника обміну повідомленнями утво рюють "погоджену пару" у тому розумінні, що вони є взаємно зворотними.
Вихідний текст шифрується відкритим ключем адресата й передається йому (рис. 20.1).
Слайд 1010
Рис. 20.1. Структурна схема криптографічної системи з відкритими ключами (асиметрична
криптографічна система)
Слайд 1111
Зашифрований текст у принципі не мо же бути розшифрований тим
же відкритим ключем.
Розшифрування повідомлення можли ве тільки з використанням закритого
клю ча, який відомий тільки самому адресатові.
Слайд 1212
1.2. Алгоритм створення ключів RSA
1. Кожний абонент системи вибирає два
випадкові прості числа p і q заданого розміру (наприклад, 512
бітів кожне).2. Обчислюється їхній добуток n = p∙q.
3. Обчислюється значення функції Ейлера від числа n:
4. Вибирається ціле число e, взаємно просте зі значенням функції φ(n). e – буде відкритим ключем криптографічної систе
Слайд 1313
ми RSA.
Звичайно в якості e беруть прості чис ла, що
містять невелику кількість одинич них бітів у двійковому записі, наприклад,
прості числа Ферма: 17, 257 або 65537.5. Обчислюється число d, мультипли кативно зворотне до числа e по модулю φ(n), що задовольняє рівнянню:
d – буде секретним ключем криптогра-фічної системи RSA.
Слайд 1414
Як видно з виразу (20.2) відкритий та секретний ключі дійсне
мультипликативно зворотні друг до друга по модулю φ(n).
6. Пари (e,
n) публікується в якості від критого ключа RSA (RSA public key).7. Пари (d, n) відіграє роль секретного ключа RSA (RSA secret key), якій тримаєть ся в секреті.
Число n називається модулем, а числа e і d - відкритої й секретної експонентами, відповідно.
Слайд 1515
Крипостійкість алгоритму RSA при ата кі на ключ базується на
складності факто ризації цілих чисел та тесту на їх простоту.
Тобто для визначення секретного ключа з виразу (20.2) по відкритому ключу потрібно знать функцію Ейлера, яка визначається згідно з (20.1) великими простимі числами p і q. Це задача достатньо важка, особливо якщо p і q мають значення довжиною біль ше 512 біт.
Слайд 1616
ВИСНОВКИ
В основу криптографічної системи з відкритим ключем RSA покладена задача
множення й розкладання складених чисел на прості співмножники, яка є
обчислю вальне односпрямованою задачею (тест простоти, факторизація).У криптографічній системі з відкритим ключем кожний учасник створює як відкри тий ключ (public key), так і секретний ключ (secret key).
Слайд 1818
2.1. Алгоритм зашифрування й
розшифрування повідомлень
за допомогою RSA
Нехай М - блок
відкритого тексту й С - відповідний блок зашифрованого тексту.
Тоді правила
зашифрування й розши фрування визначаються формулами при виконанні умови M < n :
Слайд 1919
Помітимо, що відповідно до (20.3) DK∙(C) = М.
Це випливає з
наступних міркувань. Для будь-якого цілого числа М и будь- якого простого
р справедливе рівняння Насправді, (20.4) рівносильне рівнян ню
(М р - М) mod p = 0
або рівнянню
Слайд 2020
Якщо НСД (М, p) = р, то р ділить М,
і то му М mod p = 0, звідки випливає
(20.5).Якщо ж НСД (М, р) = 1, те, згідно з ма лою теоремою Ферма, М р-1 mod p = 1, звід ки також випливає (20.5).
Згідно (20.1) і (20.2), існує ціле число r, таке, що
З (20.3) і (20.6) одержуємо наступний ланцюжок рівностей:
Слайд 2222
Оскільки р і q - різні прості числа, то на
підставі відомих властивостей порівнянь із (20.7), (20.8) одержуємо:
Звідси й випливає
коректність визна чення (20.3).Припустимо, сторона A (абонент A) прагне послати стороні B (абонентові B) повідомлення MA. Повідомлення є цілим числом, яке лежить у межах від 0 до n-1, тобто MA € Zn.
Слайд 2323
Алгоритм зашифрування повідомлення
від A до B
1. Вибрати відкритий ключ (eB,
nB) сто рони B.
2. Вибрати відкритий текст (повідом лення, число)
MA і перетворити його відпо відно до виразу(20.9)
3. Передати шифроване повідомлення абоненту B:
Слайд 2424
Алгоритм розшифрування повідомлення від A до B
1. Прийняти зашифроване повідомлен-ня
абонентом B
2. Застосувати абонентом B свого сек ретного ключа (dB,
nB) для розшифрування повідомлення:(20.10)
3. Одержати передане повідомлення:
Слайд 2626
Для обміну повідомленнями абоненти системи створюють ключі.
Нехай абонент B обирає
значення pB = 17, qB = 31.
Далі він обчислює
nB =
pB∙qB = 527і
φ(nB) = (рB - 1)∙(qB - 1) = 480.
Абонент B далі, у якості еB обирає чис ло, взаємно просте з φ(nB), наприклад еB = 7.
Слайд 2727
Для знаходження секретного ключа dB абоненту B за допомогою алгоритму
Евк ліда необхідно визначити цілі числа u і v, що
задовольняють співвідношенню480 = 7∙68 + 4; 7 = 4∙1 + 3; 4 = 3∙1 + 1;
1 = 4 - 3∙1 = 4 - (7 - 4∙1)∙1 = 4 ∙2 - 7∙1 =
= (480 - 7∙68)∙2 - 7∙ 1 = - 7∙137 + 480∙2 ,
u = -137, v = 2.
Слайд 2828
Оскільки -137 mod 480 = 343, то u = dB
= 343.
Перевірка:
(eB∙dB) mod φ(nB) = 7∙343 mod 480 =
2401 mod
480 = 1.Таким чином, відритими ключами або- ненту B будуть: eB∙= 7, nB = 527; а секрет ними: dB∙= 343, nB = 527.
Абонент A хоче передати абоненту B повідомлення MA = "RSA".
Слайд 2929
Представимо дане повідомлення у виг ляді послідовності чисел, що знаходяться
в інтервалі 0,…,526. Для цього букви R, S і А
закодуємо п’ятимірними двійковими век торами, скориставшись двійковим записом їх порядкових номерів в англійському алфавіті:R = 18 = (10010), S = 19 = (10011),
A = 1 = (00001).
Тоді RSA = (100101001100001).
Слайд 3030
Укладаючись у заданий інтервал 0,…,526, одержуємо наступне представлен ня:
RSA =
(100101001)(100001) =
= ( = 297,
= 33).Далі послідовно шифруємо:
При цьому ми скористалися тим, що
Слайд 3232
При розшифруванні абоненту B потрібно виконати наступну послідовність дій. По-
перше, обчислити
Відзначимо, що при піднесенні в сту пінь зручно скористатися
тим, що343 = 256 + 64 + 16 + 4 + 2 + 1.
На підставі цього представлення й (20.12) одержуємо:
474 1 mod 527 = 474; 474 2 mod 527 = 174;
Слайд 3333
474 4 mod 527 = 237; 474 8 mod
527 = 307;
474 16 mod 527 = 443; 474 32 mod
527 = 205;474 64 mod 527 = 392; 474 128 mod 527 = 307;
474 256 mod 527 = 443,
у силу чого
474 343 mod 527 =
= (443∙392∙443∙237∙174∙474) mod 527 = 297,
тобто
Аналогічно
407343 mod 527 = 33,
Слайд 3434
Аналогічно
407 343 mod 527 = 33,
тобто
.
Вертаючись до буквеного запису, одер жуємо
після розшифрування(MA1 = 297, MA2 = 33) =
= (100101001)(100001) = (100101001100001) =
= (10010)(10011)(00001) = (18)(19)(1) = RSA.
Слайд 3535
ВИСНОВКИ
Шифрування та розшифрування даних криптографічним алгоритмом RSA заснова не на
взаємно зворотних перетвореннях
С = Ek(M) = M e mod n;
M
= Dk(C) = C d mod n.Криптографічний алгоритм RSA у зв’яз ку з його простотою знайшов широке роз повсюдження.
Слайд 3737
Неважко показати, що складність зна ходження секретного ключа системи RSA
визначається складністю розкладання чис ла n на прості множники. У
зв'язку із цим потрібно вибирати числа р і q таким чи ном, щоб задача розкладання числа n була досить складна в обчислювальному плані. Для цього рекомендуються наступні вимо ги:1) числа р і q повинні бути досить біль шими, не занадто сильно відрізнятися друг від друга й у той же час бути не занадто близькими один одному;
Слайд 3838
2) числа р і q повинні бути такими, щоб найбільший
загальний дільник чисел p - 1 і q - 1
був невеликим; бажане, щоб НСД (p - 1, q - 1) = 2;3) р і q повинні бути сильно простими числами (сильно простим називається таке просте число r, що r + 1 має великий прос тий дільник, r - 1 має великий простий діль ник s, такий, що число s - 1 також має до сить більший простий дільник).
У випадку коли не виконане хоча б од не із зазначених умов, є ефективні алгорит ми розкладання n на прості множники.
Слайд 3939
У цей час самі більші прості числа, ви ду n
= p∙q, які вдається розкласти на множ ники відомими методами,
містять у своєму записі 140 десяткових знаків. Тому, згідно із зазначеними рекомендаціями, числа р і q у системі RSA повинні містити не менш 100 десяткових знаків.Слід підкреслити необхідність дотри мання обережності у виборі модуля RSA (числа n) для кожного з кореспондентів ме режі. У зв'язку із цим можна сказати нас тупне.
Слайд 4040
Знаючи одну із трьох величин: p, q або φ(n), можна
легко знайти секретний ключ RSA. Відомо також, що, знаючи секретну
експоненту розшифрування d, можна легко розкласти модуль n на множники. У цьому випадку вдається побудувати імовірнісний алгоритм розкладання n. Звідси випливає, що кожний кореспондент мережі, у якій для шифрування використовується система RSA, повинен мати свій унікальний мо дуль.
Слайд 4141
Насправді, якщо в мережі викорис товується єдиний для всіх модуль
n, те така організація зв'язку не забезпечує кон фіденційності, незважаючи
на те, що ба зова система RSA може бути стійкою. Ви ражаючись інакше кажучи, говорять про не спроможність протоколу із загальним мо дулем. Неспроможність випливає з того, що знання довільної пари експонент (ei, di) дозволяє, як було відзначено, розкласти n на множники. Тому будь-який кореспон дент даної мережі має можливість знайти секретний ключ будь-якого іншого корес пондента.
Слайд 4242
Більше того, це можна зробити навіть без розкладання n на
множники.
Як відзначалося раніше, системи шиф рування з відкритими ключами працюють
порівняно повільно. Дня підвищення швид кості шифрування RSA на практиці вико ристовують малу експоненту зашифру вання.Якщо вибрати число е невеликим або таким, щоб у його двійковому записі було мале одиниць, то процедуру шифрування можна значно прискорити.
Слайд 4343
Наприклад, вибравши е = 3 (при цьому ні р -
1, ні q - 1 не повинні ділитися на 3),
ми зможемо реалізувати шифрування за допо могою одного піднесення у квадрат по мо дулю n і одного перемножування. Вибрав ши е = 216 + 1 = 65537 - число, двійковий запис якого містить тільки дві 1, ми змо жемо реалізувати шифрування за допомо гою 16 піднесень у квадрат по модулю n і одного перемножування.
Слайд 4444
Якщо експонента е вибирається випад ково, то реалізація шифрування по
алго ритму RSA зажадає s піднесень у квадрат по модулю
n і в середньому s/2 множень по тому ж модулю, де s - довжина двійкового запису числа n. Разом з тим вибір неве ликої експоненти е може привести до нега тивних наслідків. Справа в тому, що в де кількох кореспондентів можуть виявитися однакові експоненти е.
Слайд 4545
Нехай, наприклад, три кореспонденти мають попарно взаємно прості модулі n1,
n2, n3 і загальну експоненту е = 3. Якщо ще
один користувач посилає їм якесь цирку лярне повідомлення М, то криптоаналітик супротивника може одержати у своє розпо рядження три шифровані текстиM3 mod ni = yi, i = 1, 2, 3.
Далі він може знайти розв'язок систе ми порівнянь
Слайд 4646
яке лежить в інтервалі 0 < y < n1∙n2∙n3. По
китайській теоремі про залишки такий роз в'язок єдиний, тому що
М3 < n1∙n2∙n3, то y = М3. Саме М можна знайти, обчислюючи кубічний корінь: Відзначимо, що вибір малої експонен ти розшифрування d також небажаний у зв'язку з можливістю визначення d прос тим перебором.
Слайд 4747
ВИСНОВКИ
Криптографічна стійкість алгоритмом RSA базується на складності факторизації чисел. Однак
за останній час з’явилися нові більш швидкодіючі методи фактори зації
чисел. Тому для підвищення крипто графічної стійкості не обхідно збільшувати значення простих чисел p і q. По оцінкам криптоаналітиків довжина цих чи сел повинна бути не менш 1024 біта, а сучасні криптостійки системи – 3072 біта. Тому, для забезпечення заданої криптостійкості використо вують асиметричні криптографічні системи, які основуються на складності дискретного логариф мування.
