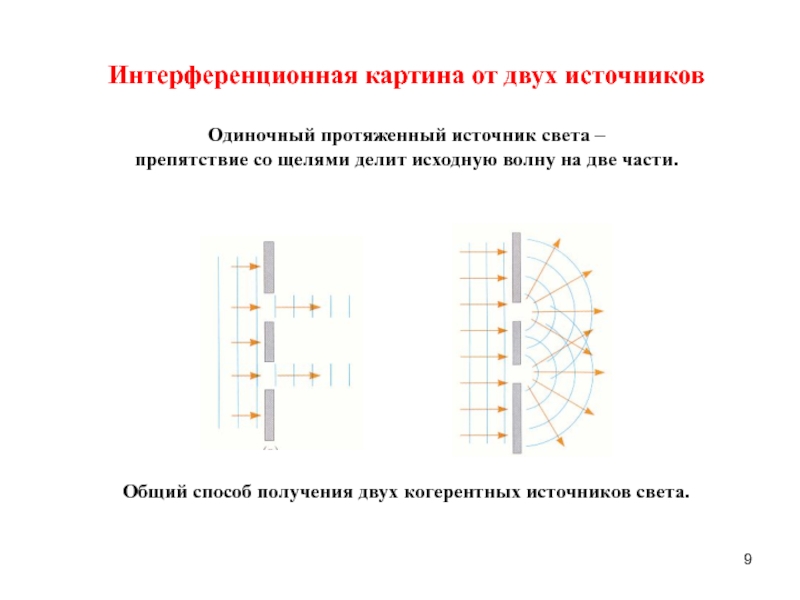
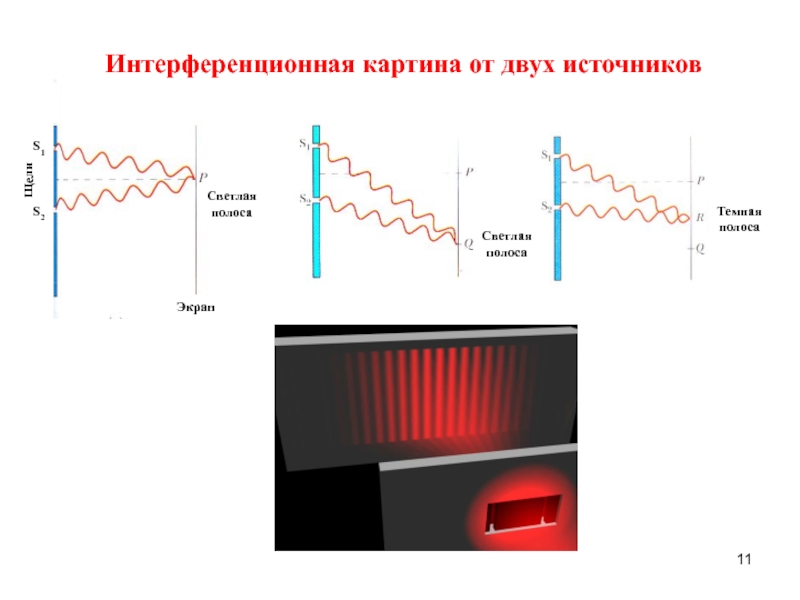
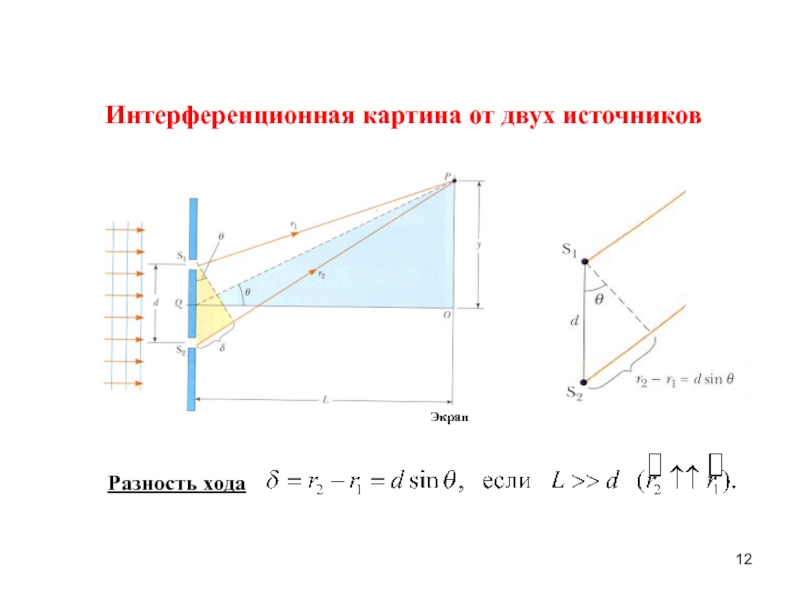
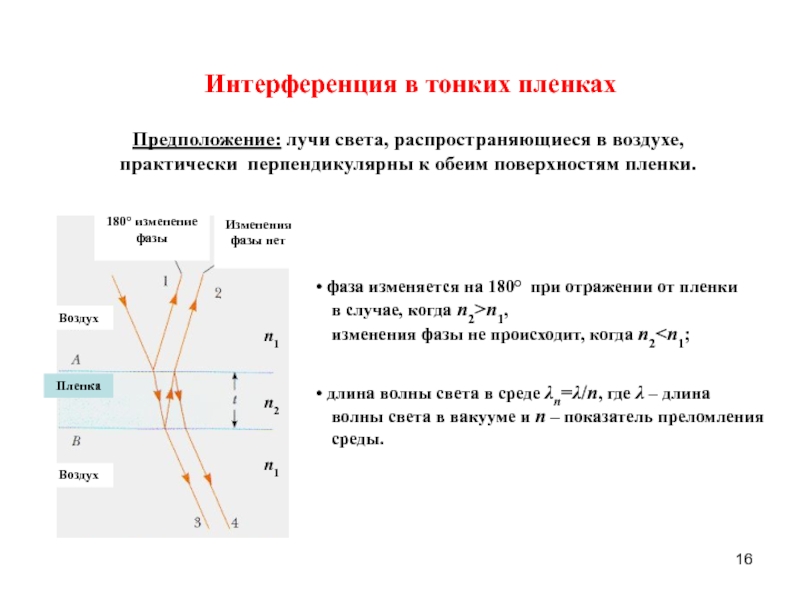
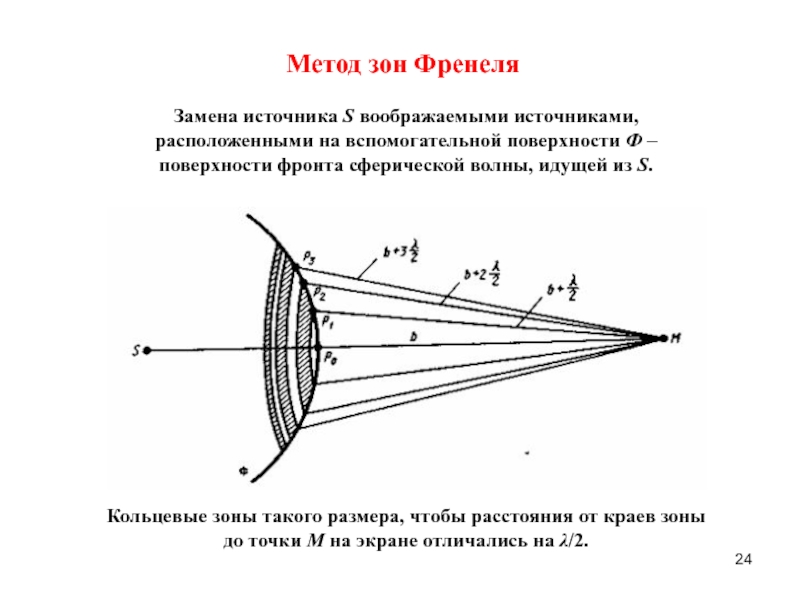
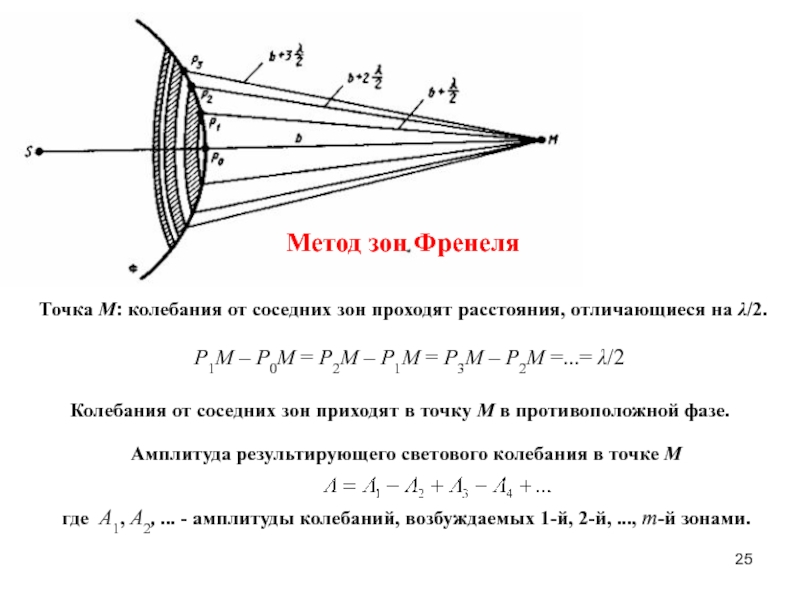
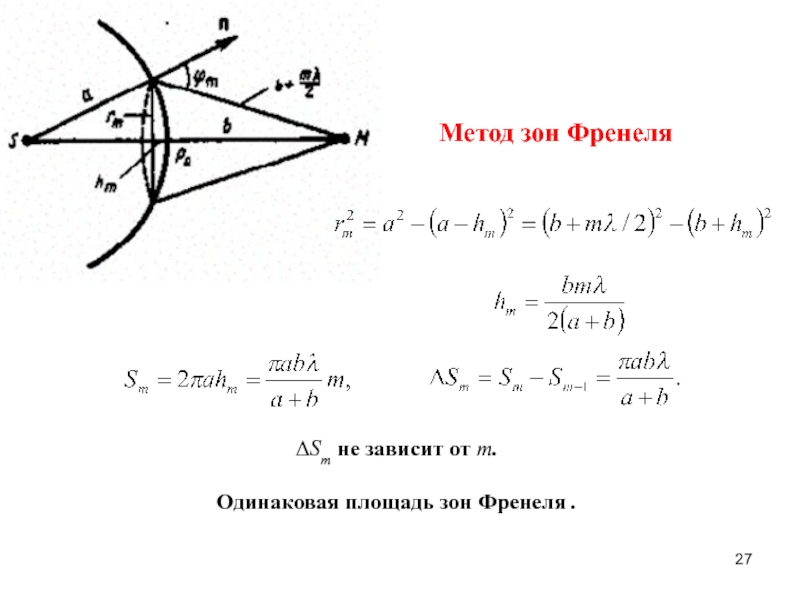
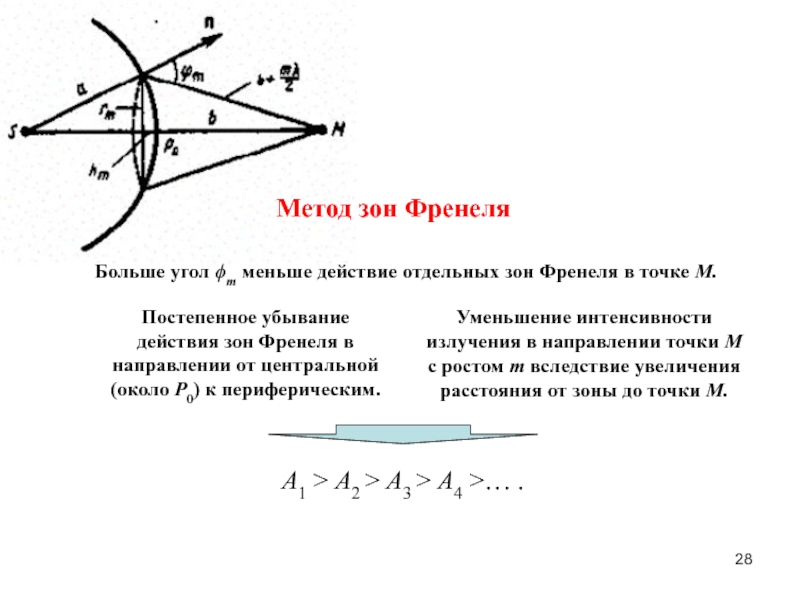
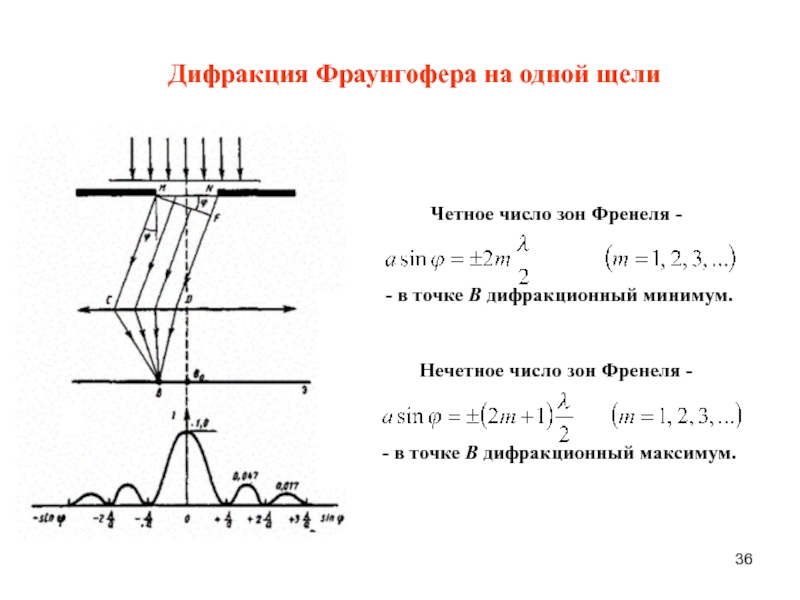
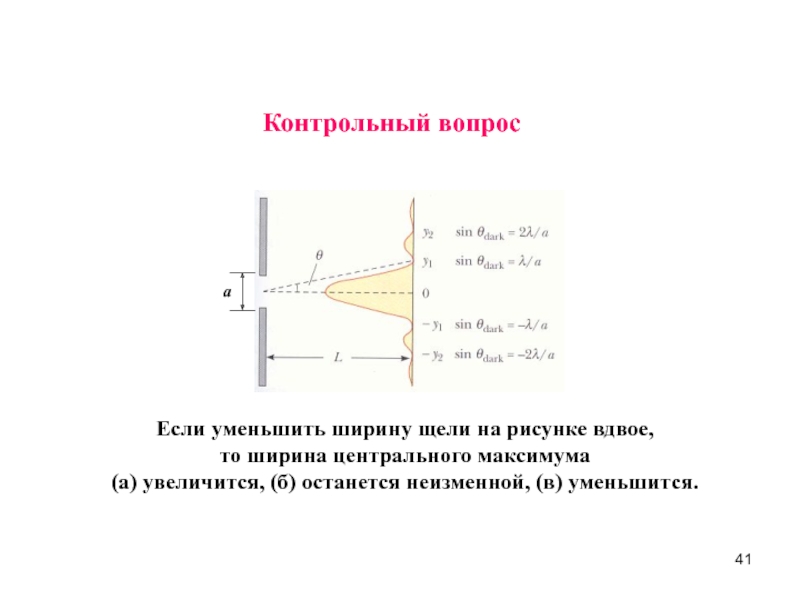
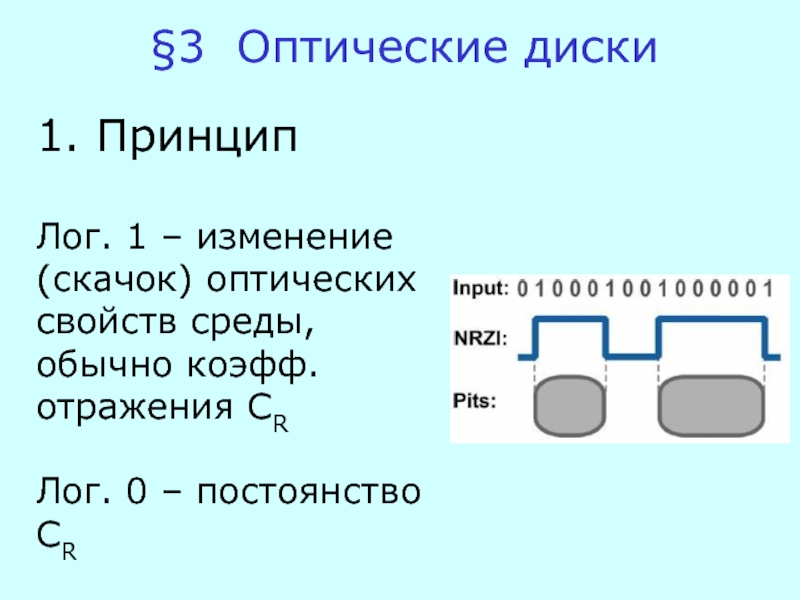
гармонический осциллятор.
Уравнение колебаний идеального осциллятора и его решение.
Свободные, затухающие, вынужденные
механические и электромагнитные колебания.Волновое движение. Длина волны, волновое число, фазовая скорость.
Волновое уравнение.
Энергетические характеристики механических и электромагнитных волн.