Слайд 12. Элементы теории вероятностей и математической статистики
Слайд 22.1. Случайные величины и их числовые характеристики
Слайд 31
Под случайной величиной понимается переменная, которая в
результате испытаний в зависимости от случая может принимать любое значение
из множества своих возможных значений.
Случайная величина называется дискретной, если множество ее возможных значений дискретно, или непрерывной, если это множество непрерывно.
Пример дискретной случайной величины: число выстрелов до первого попадания в цель.
Пример непрерывной случайной величины: - дальность полета артиллерийского снаряда.
Слайд 42
Наиболее полным и исчерпывающим описанием случайной величины
является ее закон распределения.
Законом распределения случайной величины называется
всякое соотношение, устанавливающее связь между возможными значениями случайной величины и вероятностями их реализации.
Для дискретной случайной величины закон распределения может быть задан таблицей, аналитически (в виде формулы) и графически.
Слайд 53
При табличном задании закона распределения дискретной случайной величины
первая строка таблицы содержит возможные значения, а вторая - их
вероятности.
Такая таблица называется рядом распределения дискретной случайной величины.
Сумма вероятностей во второй строке таблицы всегда равна единице, поскольку в результате испытания какое-то из возможных значений случайной величины обязательно реализуется.
Слайд 64
Пример. В денежной лотерее выпущено 100 билетов.
Разыгрывается один выигрыш 500 руб. и 10 выигрышей по 100
руб. Найти закон распределения случайной величины Х – стоимости выигрыша для владельца одного лотерейного билета.
Решение. Запишем возможные значения Х: Х1 =500; Х2 = 100; Х3 = 0. Вероятности этих возможных значений таковы: Р1 =1/100; Р2 =10/100; P3 = 89/100. Таким образом, получаем следующий закон распределения
Слайд 72.2 Математические операции над случайными величинами
Слайд 81
Определим понятие независимости случайных величин.
Две случайных
величины называются независимыми, если закон распределения одной из них не
изменяется от того, какие возможные значения приняла другая величина.
Например. Если имеются различные лотереи, то случайные величины X и Y, выражающие суммы выигрыша по билету разных лотерей, являются независимыми величинами. Если же за X и Y взять выигрыши двух различных билетов в одной лотерее, то эти величины окажутся зависимыми, так как при выигрыше одного билета вероятность выигрыша других билетов уменьшается.
Слайд 92
Математические операции над случайными величинами. Рассмотрим случайную
величину, имеющую распределение
1. Произведением kХ случайной величины Х на
постоянную величину k называется случайная величина kXi , принимающая свои значения с теми же вероятностями Pi .
2. m-ной степенью случайной величины Х
называется случайная величина принимающая свои значения с теми же вероятностями Pi .
Слайд 103
Пример. Дана случайная величина Х
Найти закон распределения случайной величины
Y=X 2
Решение. Величина Y принимает значения 1 и 4. Значение
1 она принимает с вероятностью 0,3, а значение 4 с вероятностью 0,2+0,5=0,7. Поэтому распределение величины Y имеет вид:
Слайд 114
3. Суммой (разностью или произведением) случайных величин X и Y
называется случайная величина Xi+Yi (Xi-Yi , Xi·Yi ) с
вероятностями Pij того, что величина Xi имеет вероятность Pi , а величина Yj вероятность Pj . Если случайные величины независимы, то Pij = Pi · Pj .
Пример. Даны законы распределения двух независимых случайных величин
Найти закон распределения случайной величины Z=X+Y.
Слайд 125
Решение . Величина Z может принимать следующие значения: 1 с
вероятностью P=0,18; 3 с вероятностью Р =0,12+0,42; 5 с
вероятностью Р=0,28. Поэтому закон распределения будет иметь вид:
Легко убедиться, что сумма вероятностей действительно равна 1
Слайд 132.3. Математическое ожидание дискретной случайной величины
Слайд 141
Математическим ожиданием , или средним значением, М(Х) дискретной
случайной величины Х называется сумма произведений всех ее значений на
соответствующие вероятности:
Слайд 152
Пример. Дана случайная величина Х
Требуется найти ее среднее значение.
Решение. Вычислим среднее значение в соответствии с приведенным выше определением
Слайд 163
Свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой постоянной.
M(C) =C.
2. Постоянный множитель можно выносить за знак математического ожидания:
M(kX)=kM(X).
3. Математическое ожидание суммы конечного числа случайных величин равно сумме их математических ожиданий, т.е.
Доказательство этого утверждения получить самостоятельно.
Слайд 174
4. Математическое ожидание произведения конечного числа независимых случайных величин равно
произведению их математических ожиданий.
Слайд 185
5. Математическое ожидание отклонения случайной величины от ее математического ожидания
равно нулю:
6. Если все значения случайной величины увеличить или уменьшить
на некоторое постоянное число С, то на эту же постоянную величину С изменится и математическое ожидание.
M(XC)=M(X)M(C) =M(X)C.
Доказательство этого положения следует из п. 3.
Слайд 192.4. Дисперсия дискретной случайной величины.
Слайд 201
В дальнейшем будем использовать для математического ожидания случайной
величины Х обозначение
Определение Дисперсией D(X) случайной величины Х
называется математическое ожидание квадрата ее отклонения от математического ожидания:
Слайд 212
Наряду с дисперсией вводят величину среднего квадратического отклонения
которая характеризует
степень рассеяния индивидуальных значений случайной величины от среднего значения.
Для дисперсии наряду с введенным выше обозначением D(X) используется и обозначение
которое мы будем широко применять в дальнейшем
Слайд 223
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю.
2. Изменение всех значений
признака на одну и ту же величину не изменяет величину
дисперсии.
3. Уменьшение или увеличение всех значений признака в k раз приводит к уменьшению или увеличению дисперсии в K2 раз.
4. Дисперсия алгебраической суммы или разности конечного числа независимых случайных величин равна сумме их дисперсий .
Доказательство утверждений 1– 4 необходимо произвести самостоятельно.
Слайд 234
5. Дисперсия относительно любой величины А
связана с дисперсией относительно среднего значения следующим
соотношением
Слайд 245
6. Дисперсия случайной величины равна разности между математическим ожиданием квадрата
случайной величины и квадратом ее математического ожидания. Действительно
Слайд 256
Задача. Найти дисперсию случайной величины Х, имеющей закон
распределения
Решение. Среднее значение было найдено ранее и равно –
0,3. Поэтому применяя определение дисперсии, имеем
Слайд 267
Важно! Математическое ожидание, дисперсия и среднее квадратическое отклонения, характеризуя
случайную величину, сами случайными величинами не являются.
Если случайной
величиной является доходность некоторых акций, то средняя величина характеризует прогнозируемую доходность, а среднее квадратическое отклонение – меру колеблемости доходов от среднего значения т.е. риск данного актива.
Слайд 272.5. Функция распределения непрерывной случайной величины
Слайд 281
Задание закона распределения в виде таблицы неприменимо для непрерывных
случайных величин.
Возможен другой подход при котором задается вероятность
того, что случайная величина Х примет значение меньшее чем х.
Определение. Функцией распределения случайной величины Х называется функция F(x) , которая для каждого значения х определяет вероятность того, что случайная величина Х примет значение меньшее нежели х . Эту величину называют иногда интегральной функцией распределения.
Слайд 292
Рассмотрим общие свойства функции распределения.
1. Функция распределения случайной величины
есть положительно определенная неубывающая функция, значения которой заключены между нулем
и единицей:
Слайд 303
2. Вероятность попадания случайной величины в интервал значений [x1
, x2 ] (включая х1) равна приращению функции распределения на
этом интервале
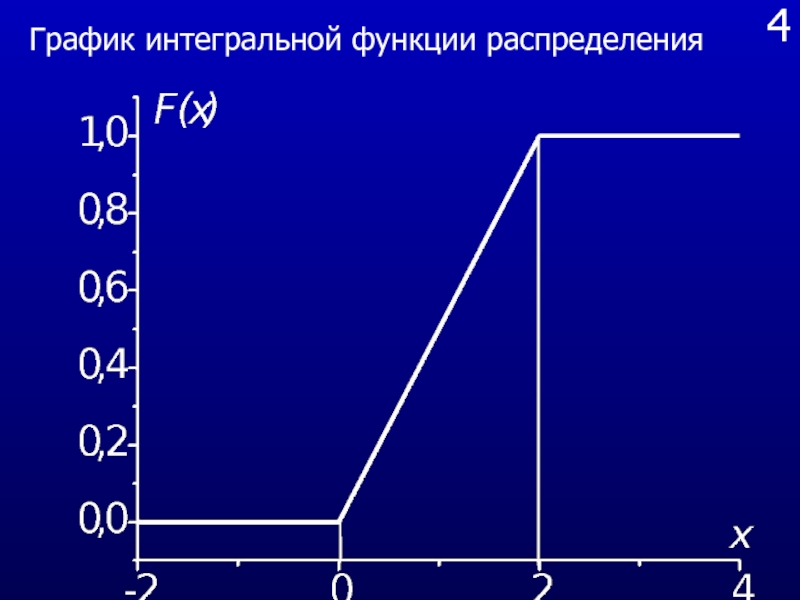
Задача. Функция распределения случайной величины имеет вид
Найти вероятность того, что случайная величина примет значение в интервале [1; 3].
Слайд 314
График интегральной функции распределения
Слайд 325
Решение. Исходя из определения имеем:
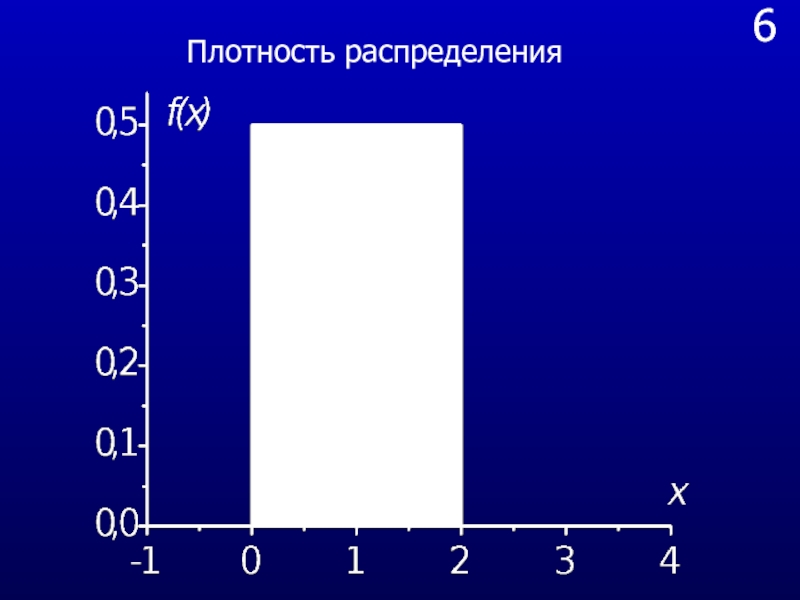
Для непрерывной случайной величины чаще
задается не функция распределения F(x) , а другая величина, которая
называется плотностью вероятности или плотностью распределения.
Функция плотности вероятности случайной величины Х определяется выражением
Слайд 351
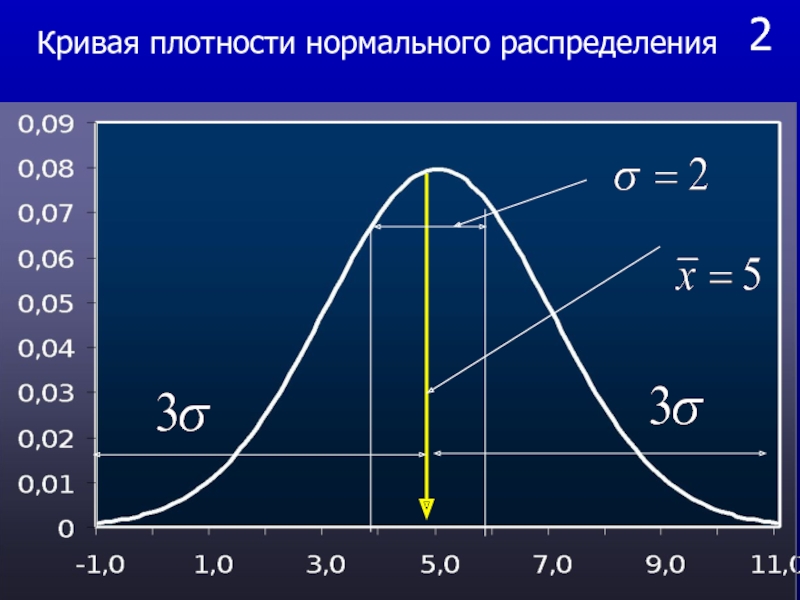
Нормальное распределение широко используется в математической
статистике как предполагаемое теоретическое распределение. Оно зависит от двух параметров
и и определяется с помощью следующей функции для плотности распределения:
Слайд 362
Кривая плотности нормального распределения
Слайд 373
1. Нормальное распределение является симметричным относительно прямой
.
2. Кривая имеет горизонтальную асимптоту – ось абсцисс
(при х кривая приближается к оси абсцисс).
3. Кривая имеет максимум в точке , который равен
Свойства нормального распределения
Слайд 384
4. Площадь между осью абсцисс и кривой нормального распределения
равна единице.
5. В промежутке между значениями
содержится 99,73% всей
площади кривой, а это означает, что 99,73% всех членов совокупности сосредоточены в этом интервале, если распределение нормальное
Слайд 395
Найдем вероятность попадания случайной величины распределенной нормально в интервал
значений от х1 до х2 . В соответствии общим определением
функции плотности распределения находим:
Преобразуем это выражение, вводя новую переменную интегрирования
Слайд 417
Введем в рассмотрение функцию Лапласа, которая определяется выражением
Используя это
определение, очевидно, получаем
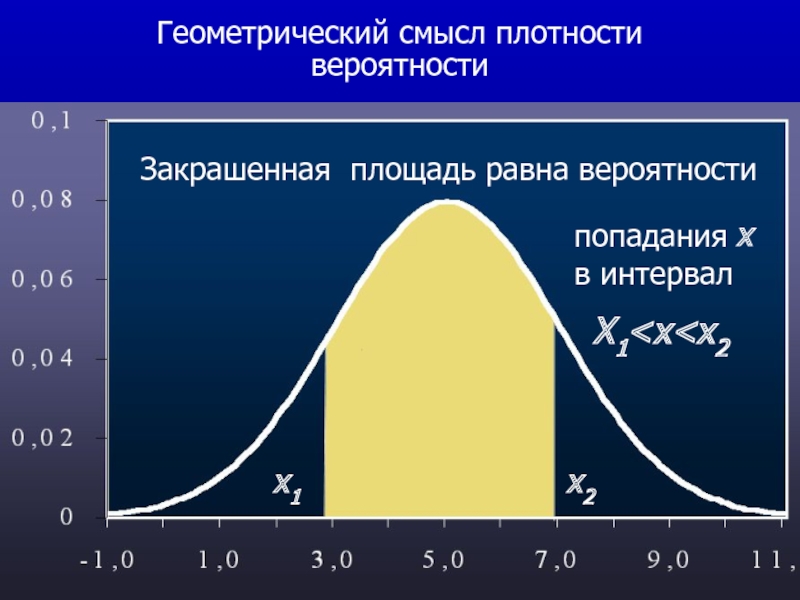
Геометрически искомая вероятность представляет собой площадь между
ординатами х1 и х2 и кривой.
Слайд 42Геометрический смысл плотности вероятности
х1
х2
Закрашенная площадь равна вероятности
попадания х в интервал
Х1
Слайд 43 2.7 Универсальные распределения
Слайд 449
Рассмотрим несколько основных законов распределения, составляющий необходимый
математический аппарат для построения в дальнейшем статистических критериев и оценок,
применяемых в эконометрике.
Причиной, по которым они играют заметную роль в статистике, является их универсальность. Для их построения не нужно задавать параметры, как для нормального распределения. Они однозначно определяются лишь параметрами, которые обычно известны.
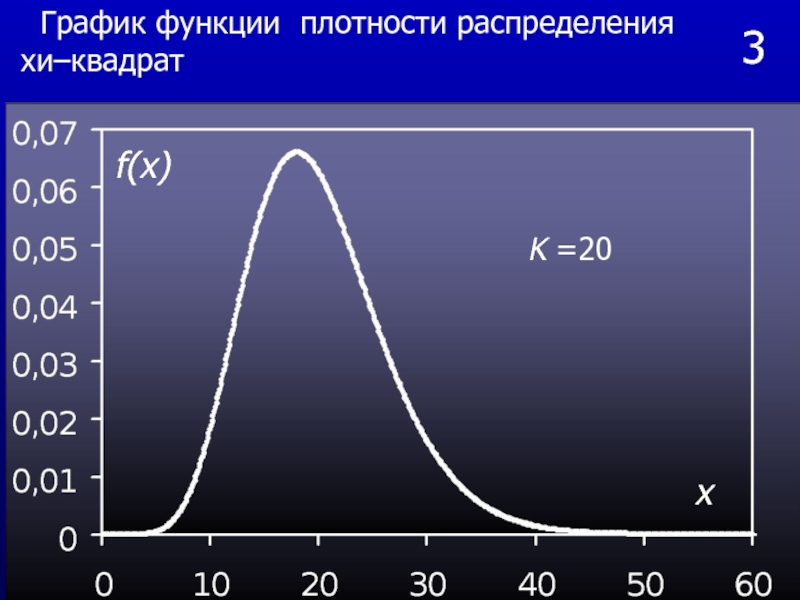
Слайд 45 Распределение (хи-квадрат)
Распределением
(хи-квадрат) с к степенями свободы называется распределение суммы квадратов
к независимых случайных величин, распределенных по стандартному нормальному закону
где случайные величины Zi ( i = 1,2,…k) имеют нормальное распределение с математическим ожиданием равным 0 и дисперсией равной 1.
Слайд 462
Функция плотности распределения хи-квадрат зависит лишь только от
одного параметра – числа степеней свободы.
Числом степеней свободы
k распределения называется число независимых значений случайной величины. Это число равно числу наблюдений (вариантов) n за вычетом числа уравнений связи L, которые накладываются на эти наблюдения. Например, если величины Xi связаны линейным соотношением
тогда число степеней свободы k будет равным n-1 .
Слайд 473
K =20
x
f(x)
График функции плотности распределения хи–квадрат
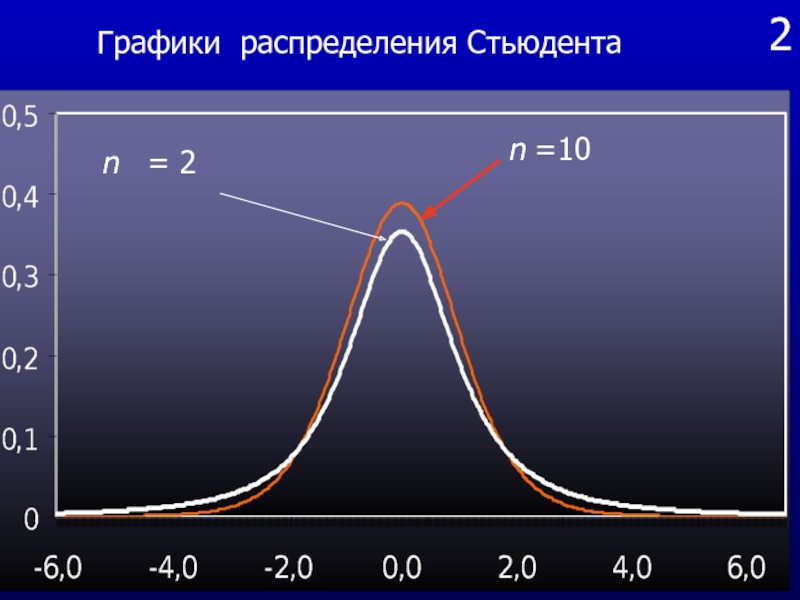
Слайд 48 Распределение Стьюдента
Распределением Стьюдента или t – распределением называется
распределение случайной величины
где Z – случайная величина, имеющая стандартное
нормальное распределение с математическим ожиданием
равным нулю и дисперсией равной единице.
независимая от Z случайная величина, имеющая распределение хи-квадрат с k степенями свободы.
Слайд 492
n =10
n = 2
Графики распределения Стьюдента
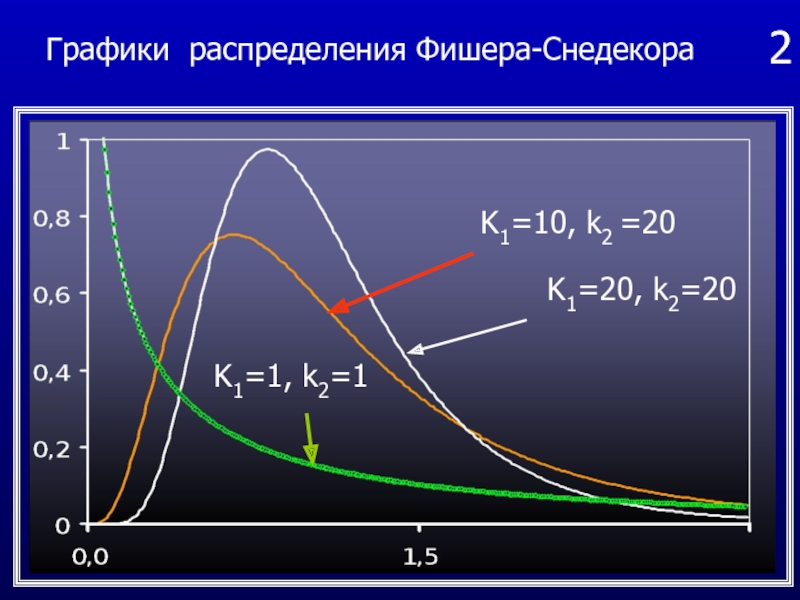
Слайд 50Распределение Фишера–Снедекора
Распределением Фишера-Снедекора или F – распределением называется
распределение случайной величины
Слайд 512
K1=20, k2=20
K1=10, k2 =20
K1=1, k2=1
Графики распределения Фишера-Снедекора





























![2. Элементы теории вероятностей и математической статистики 3 2. Вероятность попадания случайной величины в интервал значений [x1 , 3 2. Вероятность попадания случайной величины в интервал значений [x1 , x2 ] (включая х1) равна приращению](/img/thumbs/d553084811d3628b7330c5f4b2612674-800x.jpg)