2. Классификация кристаллов по симметрийным свойствам 2.1. Кристаллографическое

отсчета)
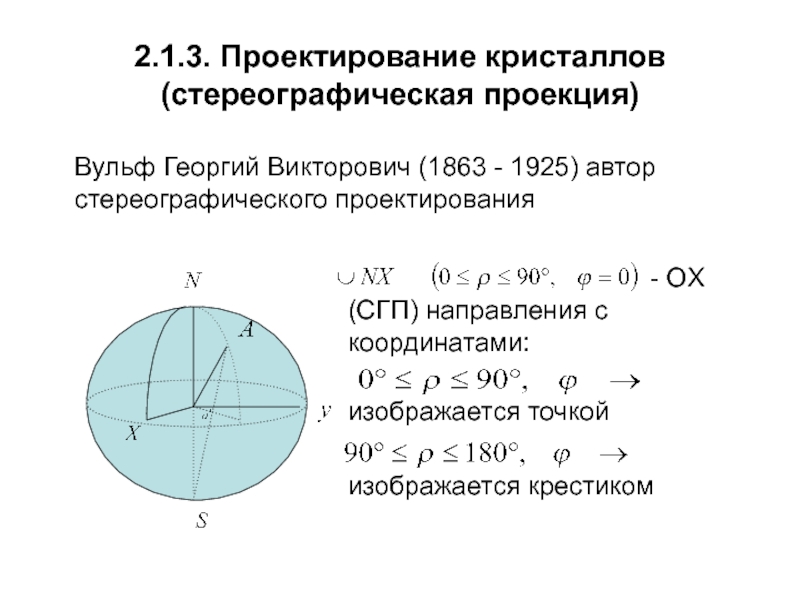
сфера единичного радиуса R=1;
полярное расстояние

;
долгота .
Сечение сферы, отвечающее сферическим координатам , получило название нулевого меридиана.
Сечение сферы, отвечающее координатам
, получило название экваториального сечения.

с общей осью зоны ОХ.

б) Стереографические проекции пересечений со сферой

системы аксиальных конусов, у которых общая ось ОХ.

введены на основе изучения форм реальных кристаллов (их естественной огранки).

Законы

компликации (сочетание различных кристаллографических форм) были результатом обобщения идеализированных форм кристаллических многогранников.
Современная наука о классификации кристаллических материалов по симметрийным свойствам базируется на представлениях о симметрии структуры кристаллов.

при котором происходит самосовмещение пространственной структуры кристалла (операция симметрии).

Шефталь Н.Н.:

«симметрия есть равное размещение равных частей».

Если такие преобразования существуют, то говорят о наличии симметрии.

Элемент симметрии: геометрическое место точек пространства кристалла инвариантных при симметрийном преобразовании (геометрические образы, с помощью которых достигается симметрийное преобразование.)

Элементы симметрии первого рода связывают между собой конгруэнтно равные фигуры, либо их части.

Детерминант матричного представления оператора симметрии первого рода равен (+1).

зеркальное отображение.
Определитель матрицы оператора элемента симметрии второго рода равен (-1).
Явление

энантиоморфизма: наличие в природе зеркально равных объектов.
Нарушение паритетности правых и левых форм в биологии (проблема киральности); в антропогенной среде (правая и левая аккомодация двигательных центров).

порядок оси симметрии)

Научная литература: обозначают арабской цифрой,

отвечающей порядку оси симметрии.






Задача:
Для кристаллических тел возможны только оси симметрии ( - запрещены).

плоскость относительно которой инвариантными оказываются объект и его зеркальное отражение.

; p – учебная m - научная
Стереографические проекции плоскостей симметрии

пространственной системе координат, относительно которой объект и его симметрийный образ

зеркально равны.
Обозначения:
C, I – учебная
I – научная.

порядка (2n+1) представляют собой сочетание поворотной оси симметрии такого же

порядка и центра инверсии;

инверсионные оси симметрии нечетно-четного порядка 2 (2n+1) являются сочетанием поворотной оси симметрии вдвое меньшего порядка и перпендикулярной ей плоскости симметрии;

инверсионные оси симметрии четно-четного порядка 2 (2n) являются уникальными и на простые элементы симметрии не раскладываются.