Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
21.2. ДУ ПЕРВОГО ПОРЯДКА Уравнение вида называется ДУ первого порядка. Где х –
Содержание
- 1. 21.2. ДУ ПЕРВОГО ПОРЯДКА Уравнение вида называется ДУ первого порядка. Где х –
- 2. Если из уравнения можно выразить производную неизвестной
- 3. Решением ДУ первого порядка называетсяфункция у=φ(х), определенная
- 4. ТЕОРЕМА КОШИ(о существовании и единственности решения ДУ)Пусть
- 5. заключается в том, что график решения ДУ
- 6. Задача решения уравнения (2), удовлетворяющего условию (3)
- 7. уравнения (2) называется функция удовлетворяющая этому
- 8. Рассмотрим уравнениеПравая часть уравнения удовлетворяет всем условиям
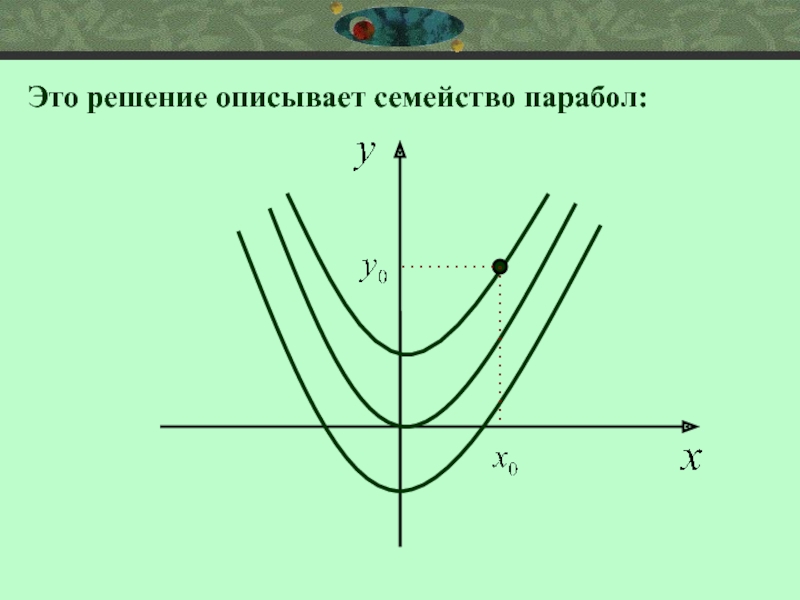
- 9. Это решение описывает семейство парабол:
- 10. Для нахождения частного решения зададим начальные условия
- 11. Скачать презентанцию
Если из уравнения можно выразить производную неизвестной функции, то оно примет вид:2Это уравнение называется ДУ первого порядка, Например:разрешенным относительно первой производной
Слайды и текст этой презентации
Слайд 121.2. ДУ ПЕРВОГО ПОРЯДКА
Уравнение вида
называется ДУ первого порядка.
Где х –
независимая переменная;
Слайд 2Если из уравнения можно выразить производную неизвестной функции, то оно
примет вид:
2
Это уравнение называется ДУ первого порядка,
Например:
разрешенным относительно первой
производнойСлайд 3Решением ДУ первого порядка называется
функция у=φ(х), определенная на
некотором интервале (a,b),
которая
при подстановке ее в уравнение
обращает его в тождество.
Слайд 4ТЕОРЕМА КОШИ
(о существовании и единственности решения ДУ)
Пусть дано ДУ (2).
Если функция f(x,y) и ее
частная производная f‘y(x,y) непрерывны
в некоторой области
D плоскости ХОУ,то в некоторой окрестности любой
внутренней точки (х0,у0) этой области
существует единственное решение этого
уравнения, удовлетворяющего условию
х=х0, у=у0.
Слайд 5заключается в том, что график решения ДУ есть интегральная кривая.
В области D содержится бесконечно много интегральных кривых. Теорема гарантирует,
что при соблюдении определенных условий через каждую внутреннюю точку области проходит только одна интегральная кривая.Условия, задающие значения функции в фиксированной точке называются начальными условиями (условиями Коши):
3
геометрический смысл теоремы Коши
Слайд 6Задача решения уравнения (2), удовлетворяющего условию (3) называется задачей Коши.
(из
множества интегральных кривых выделяется та, которая проходит через заданную точку).
В
некоторых случаях, если условия теоремы Коши не выполнены, через точку вообще не проходит интегральная кривая, или их проходит несколько.Такие точки называются
особыми точками ДУ
Слайд 7 уравнения (2) называется функция
удовлетворяющая этому уравнению при произвольном
значении С.
уравнения (2) называется функция
полученная при определенном значении С=С0.
общим решением
частным
решениемСлайд 8Рассмотрим уравнение
Правая часть уравнения удовлетворяет всем условиям теоремы Коши во
всех точках плоскости ХОУ:
Функции f(x,y)=2x и f‘y=0 определены и непрерывны
на всей плоскости.Общее решение уравнения:
Пример.