Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
22.3. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО На некотором множестве точек,
Содержание
- 1. 22.3. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО На некотором множестве точек,
- 2. Если каждой точке z соответствует одно значение
- 3. Пример.Функция-однозначна. Ее можно считать определенной на всей
- 4. Функция-многозначна. Она определена с точностью до 2П
- 5. Поскольку задание комплексного числа равносильно заданию двух
- 6. Пример.Задана функцияПри имеем:
- 7. Если значения аргумента z изображать точками на
- 8. а G – множество точек плоскости W,
- 9. Слайд 9
- 10. Пример.Функцияотображает круг g плоскости Z с радиусом
- 11. Если в плоскости Z кривая С задана
- 12. Пример.Найти образ прямойпри отображении
- 13. Решение.Уравнение равносильно системе уравнений следовательно- биссектриса 1-го координатного угла
- 14. С помощью функцииэта прямая отображается на линию- биссектриса 2-го координатного угла
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 122.3. ФУНКЦИИ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
На некотором множестве точек, изображающих значения комплексного переменного
z задана функция
в соответствие одно или несколько значений ω.Слайд 2Если каждой точке z соответствует одно значение ω, то функция
называется однозначной.
Если каждой точке z соответствует несколько значений ω, то
функция называется многозначной.
Слайд 3Пример.
Функция
-однозначна.
Ее можно считать определенной на всей плоскости, т.к. по
формуле введения комплексного числа в степень, любому комплексному числу z
ставится в соответствие одно значение z2.1
Слайд 4Функция
-многозначна.
Она определена с точностью до 2П и определена на
всей плоскости, кроме точки z=0 (при z=0 Argz не имеет
смысла).2
Слайд 5Поскольку задание комплексного числа равносильно заданию двух действительных чисел x
и y:
то числу ω тоже однозначно соответствует пара действительных чисел
u и v:Поэтому зависимость
между комплексной функцией ω и комплексным аргументом z равносильна зависимости:
определяющей действительные величины u и v как функции действительных аргументов х и у.
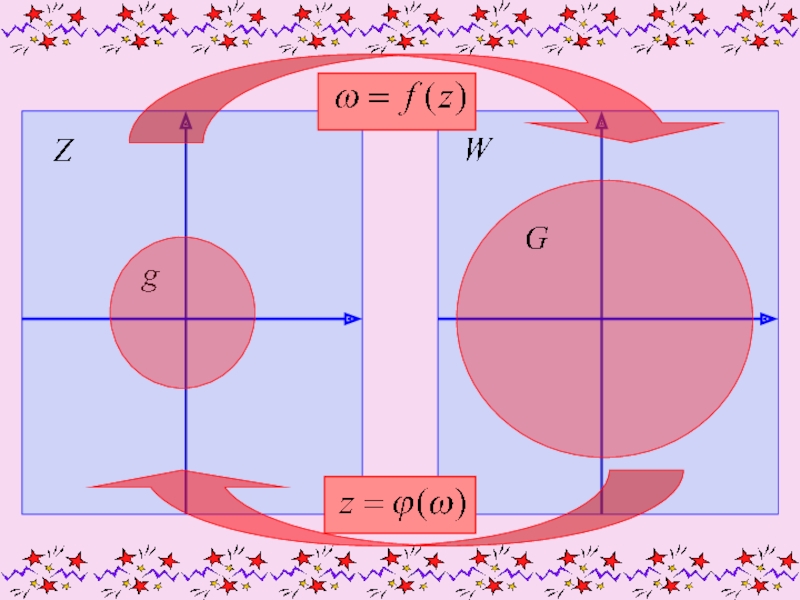
Слайд 7Если значения аргумента z изображать точками на плоскости Z, а
значения функции ω – точками на плоскости W, то функция
устанавливает
зависимость между точками плоскости Z, в которых эта функция определена, и точками плоскости W.Таким образом устанавливается отображение точек плоскости Z на соответствующие точки плоскости W.
Пусть g – множество точек плоскости Z, на которых определена функция
Слайд 8а G – множество точек плоскости W, на которое отображаются
точки функции
Каждой точке множества G будет соответствовать одна или
несколько точек множества g. Это будет означать, что на множестве G определена некоторая функция Эта функция будет обратной к функции
Если функция
однозначна., то и обратная к ней функция будет однозначной, если отображение
взаимно однозначно.
Слайд 10Пример.
Функция
отображает круг g плоскости Z с радиусом 2 на круг
G плоскости ω с радиусом 4.
Это отображение однозначно, но не
взаимно однозначно, поскольку функция - однозначна, и каждой точке плоскости Z соответствует одна точка плоскости ω.
Но каждой точке плоскости ω, соответствуют две точки плоскости Z, следовательно функция
осуществляющая отображение области G в g – двузначна.
Слайд 11Если в плоскости Z кривая С задана уравнением
то чтобы
найти уравнение кривой в плоскости ω, на которую отображается кривая
С, нужно исключить х и у из уравненийто подставляя эти выражения вместо х и у , получим:
Если кривая С задана параметрически: