Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
2.4. Дальность видимости горизонта и ориентиров в море
Содержание
- 1. 2.4. Дальность видимости горизонта и ориентиров в море
- 2. 2.4.1. Дальность видимости горизонта Наблюдаемая в море
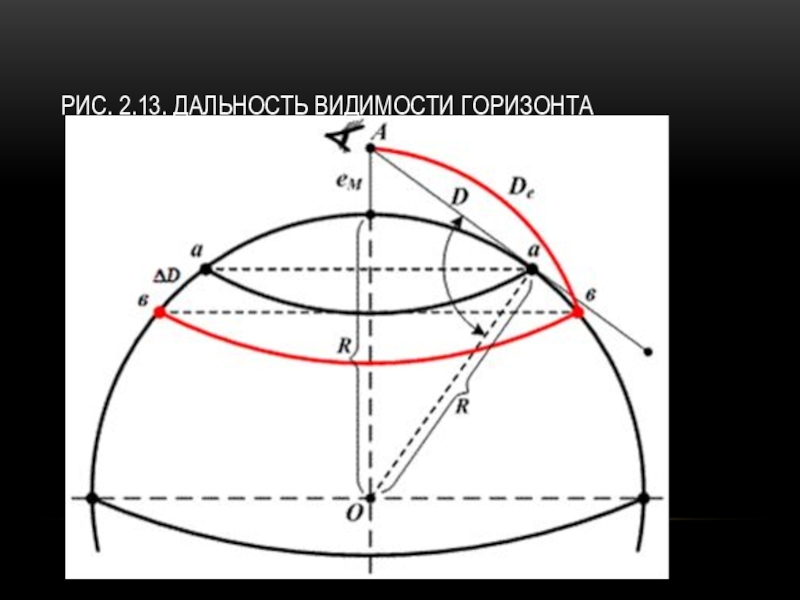
- 3. Рис. 2.13. Дальность видимости горизонта
- 4. ПРОДОЛЖЕНИЕНаблюдаемая в море линия, по которой море
- 5. ПРДОЛЖЕНИЕТак как величина чрезвычайно
- 6. ПРОДОЛЖЕНИЕПо формуле (2.8) составлена таблица № 22
- 7. 2.4.2. Дальность видимости ориентиров в море Если
- 8. Формула (2.9) решается с помощью таблицы 22
- 9. Формулу (2.9) можно решать и с помощью
- 10. Географическая дальность видимости предметов (из табл. 2.3. «МТ-2000»)Таблица 2.3.
- 11. 2.4.3. Дальность видимости огня ориентира, показанная на карте
- 12. . Дальности видимости огня маякаDK = Dh
- 13. ПРОДОЛЖЕНИЕDO = DK + ΔDKΔDK = De
- 14. Выводы Основными для наблюдателя являются: плоскости: плоскость
- 15. ПРДОЛЖЕНИЕДальность видимости навигационного ориентира (днем в хорошую
- 16. для расчёта дальности видимости в киломметрах.
- 17. шпаргалка
- 18. Скачать презентанцию
2.4.1. Дальность видимости горизонта Наблюдаемая в море линия, по которой море как бы соединяется с небосводом, называется видимым горизонтом наблюдателя. Если глаз наблюдателя находится на высоте еМ над уровнем моря (т.
Слайды и текст этой презентации
Слайд 22.4.1. Дальность видимости горизонта
Наблюдаемая в море линия, по которой море
как бы соединяется с небосводом, называется видимым горизонтом наблюдателя. Если глаз
наблюдателя находится на высоте еМ над уровнем моря (т. А рис. 2.13), то луч зрения идущий по касательной к земной поверхности, определяет на земной поверхности малый круг аа, радиуса D.Слайд 4ПРОДОЛЖЕНИЕ
Наблюдаемая в море линия, по которой море как бы соединяется
с небосводом, называется видимым горизонтом наблюдателя. Если глаз наблюдателя находится на
высоте еМ над уровнем моря (т. А рис. 2.13), то луч зрения идущий по касательной к земной поверхности, определяет на земной поверхности малый круг аа, радиуса D.Это было бы верно, если бы Землю не окружала атмосфера.
Если принять Землю за шар и исключить влияние атмосферы то, из прямоугольного треугольника ОАа следует: ОА=R+e
Слайд 5ПРДОЛЖЕНИЕ
Так как величина чрезвычайно мала (для е
= 50м при R = 6371км – 0,000004), то окончательно
имеем:(2.6)
Под действием земной рефракции, в результате преломления зрительного луча в атмосфере, наблюдатель видит горизонт дальше (по кругу вв).
(2.7)
где х – коэффициент земной рефракции (≈ 0,16).
Если принять дальность видимого горизонта De в милях, а высоту глаза наблюдателя над уровнем моря (еМ) в метрах и подставить значение радиуса Земли (R=3437,7 мили = 6371 км), то окончательно получим формулу для расчета дальности видимого горизонта
(2.8)
Например: 1) е = 4 м De = 4,16 мили; 2) е = 9 м
De = 6,24 мили;
3) е = 16 м De = 8,32 мили; 4) е = 25 м De = 10,4 мили.
Слайд 6ПРОДОЛЖЕНИЕ
По формуле (2.8) составлена таблица № 22 «МТ-75» (с. 248)
и таблица № 2.1 «МТ-2000» (с. 255) по (еМ) от
0,25 м ÷ 5100 м. (см. табл. 2.2)Географическая дальность видимого горизонта (из табл. 2.2. «МТ-75» или 2.1. «МТ-2000»)
Таблица 2.2.
Слайд 72.4.2. Дальность видимости ориентиров в море
Если наблюдатель, высота глаза которого
находится на высоте еМ над уровнем моря (т. А рис.
2.14), наблюдает линию горизонта (т. В) на расстоянии Dе(миль), то, по аналогии, и с ориентира (т. Б), высота которого над уровнем моря hМ, видимый горизонт (т. В) наблюдается на расстоянии Dh(миль).Рис. 2.14. Дальность видимости ориентиров в море
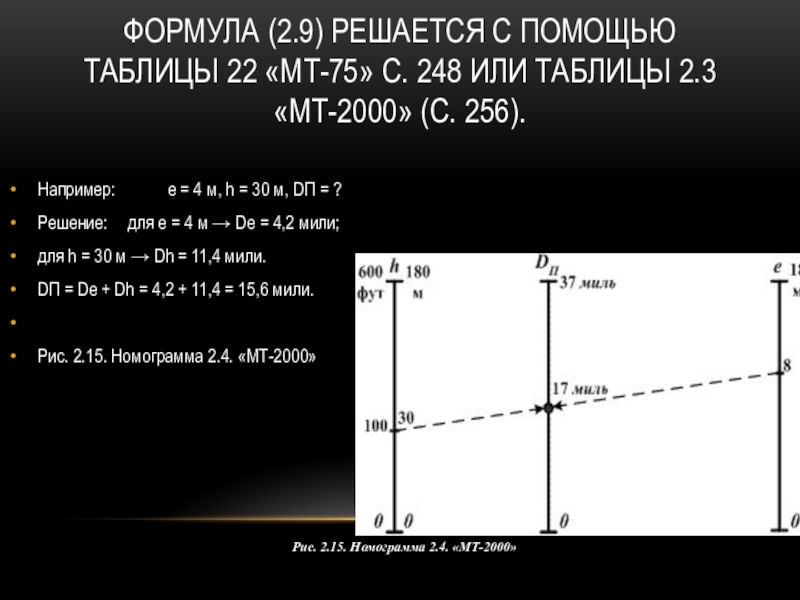
Слайд 8Формула (2.9) решается с помощью таблицы 22 «МТ-75» с. 248
или таблицы 2.3 «МТ-2000» (с. 256).
Например: е =
4 м, h = 30 м, DП = ?Решение: для е = 4 м → Dе = 4,2 мили;
для h = 30 м → Dh = 11,4 мили.
DП = Dе + Dh = 4,2 + 11,4 = 15,6 мили.
Рис. 2.15. Номограмма 2.4. «МТ-2000»
Рис. 2.15. Номограмма 2.4. «МТ-2000»
Слайд 9Формулу (2.9) можно решать и с помощью Приложения 6 к
«МТ-75» или номограммы 2.4 «МТ-2000» (с. 257) → рис. 2.15. Например:
е = 8 м, h = 30 м, DП = ? Решение: Значения е = 8 м (правая шкала) и h = 30 м (левая шкала) соединяем прямой линией. Точка пересечения этой линии со средней шкалой (DП) и даст нам искомую величину 17,3 миль. (см. табл. 2.3).Слайд 12. Дальности видимости огня маяка
DK = Dh + De=5м =
Dh + 4,7 мили
Если же действительная высота глаза наблюдателя над
уровнем моря отличается от 5 м, то для определения дальности видимости огня ориентира необходимо к дальности, показанной на карте (в пособии), прибавить (если е > 5 м), или отнять (если е < 5 м) поправку к дальности видимости огня ориентира (ΔDK), показанной на карте за высоту глаза.Слайд 13ПРОДОЛЖЕНИЕ
DO = DK + ΔDK
ΔDK = De − De=5м =
De − 4,7 мили = 2,08 · √е− 4,7 мили
Например: DK
= 20 миль, е = 9 м.
ΔDK = 2,08 · √е− 4,7 = 6,24 − 4,7 = 1,54 мили
тогда: DO = DK + ΔDK = 20,0 + 1,54 = 21,54 мили Ответ:DO = 21,54 мили.
Слайд 14Выводы
Основными для наблюдателя являются:
плоскости:
плоскость истинного горизонта наблюдателя (пл.
ИГН);
плоскость истинного меридиана наблюдателя (пл. ИМН);
плоскость первого вертикала наблюдателя;
линии:
отвесная
линия (нормаль) наблюдателя,линия истинного меридиана наблюдателя → полуденная линия N-S;
линия Е-W.
Системами счета направлений являются:
круговая (0°÷360°);
полукруговая (0°÷180°);
четвертная (0°÷90°).
Любое направление на поверхности Земли может быть измерено углом в плоскости истинного горизонта, принимая за начало отсчета линию истинного меридиана наблюдателя.
Истинные направления (ИК, ИП) определяются на судне относительно северной части истинного меридиана наблюдателя, а КУ (курсовой угол) – относительно носовой части продольной оси судна.
Дальность видимого горизонта наблюдателя (De) рассчитывается по формуле: