Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
30. Правильная пирамида
Содержание
- 1. 30. Правильная пирамида
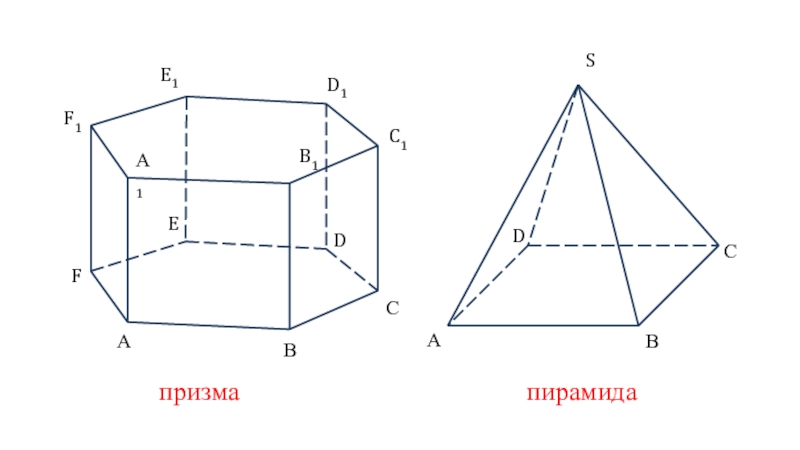
- 2. АВСDEFА1B1C1D1F1E1АВСDSпризмапирамида
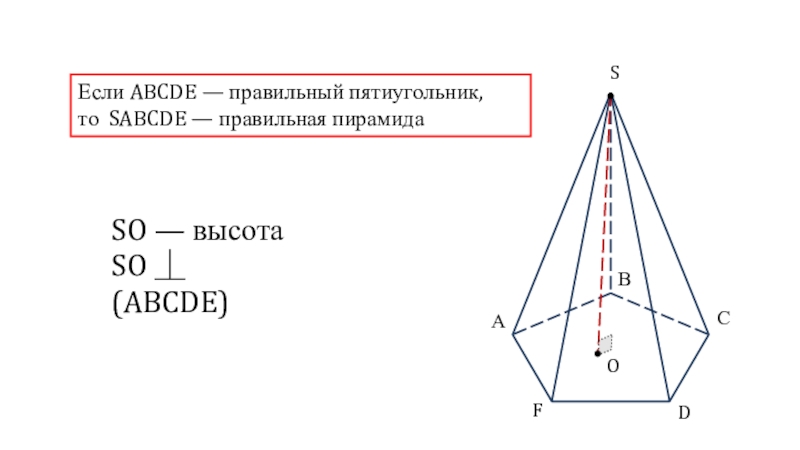
- 3. Если ABCDE — правильный пятиугольник, то SABCDE — правильная пирамидаSO — высотаSO ⏊ (ABCDE)АВСDFSO
- 4. PA1A2…An — правильная пирамидаА1Р — боковое реброΔА1РО
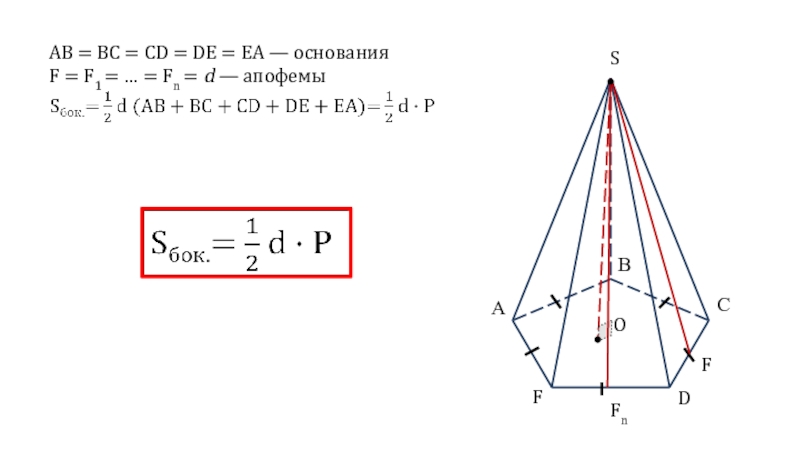
- 5. АВСDESOFMВсе апофемы правильной пирамиды равны, а так
- 6. АВСDFSOАВ = ВС = CD = DE
- 7. Задача 1SABCD — правильная пирамидаДано:SA = 12
- 8. Задача 2DABC — правильная пирамидаДано:(ABC)^(DBC) = 45°Решение:DABC
- 9. Скачать презентанцию
АВСDEFА1B1C1D1F1E1АВСDSпризмапирамида
Слайды и текст этой презентации
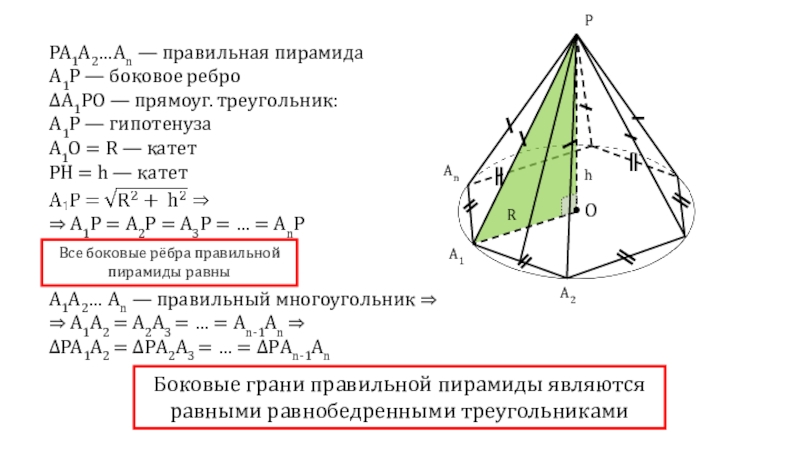
Слайд 4PA1A2…An — правильная пирамида
А1Р — боковое ребро
ΔА1РО — прямоуг. треугольник:
А1Р
— гипотенуза
А1О = R — катет
РН = h — катет
⇒
A1P = A2P = A3P = … = AnP Все боковые рёбра правильной пирамиды равны
P
An
A1
A2
h
О
R
A1A2… An — правильный многоугольник ⇒
⇒ A1A2 = А2А3 = … = Аn-1An ⇒
ΔPA1A2 = ΔPА2А3 = … = ΔPАn-1An
Боковые грани правильной пирамиды являются равными равнобедренными треугольниками
Слайд 5А
В
С
D
E
S
O
F
M
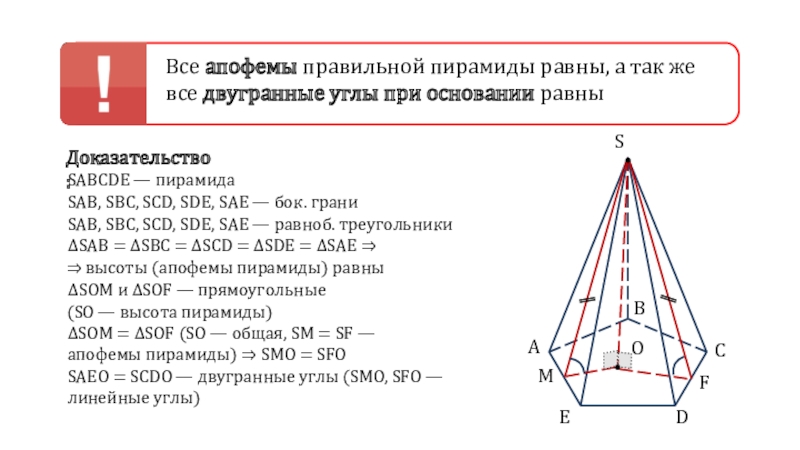
Все апофемы правильной пирамиды равны, а так же все двугранные
углы при основании равны
Доказательство:
SABCDE — пирамида
SAB, SBC, SCD, SDE,
SAE — бок. граниSAB, SBC, SCD, SDE, SAE — равноб. треугольники
ΔSAB = ΔSBC = ΔSCD = ΔSDE = ΔSAE ⇒
⇒ высоты (апофемы пирамиды) равны
ΔSОМ и ΔSОF — прямоугольные
ΔSОМ = ΔSОF (SO — общая, SM = SF —
апофемы пирамиды) ⇒ SMO = SFO
SAEO = SCDO — двугранные углы (SMO, SFO — линейные углы)
(SO — высота пирамиды)
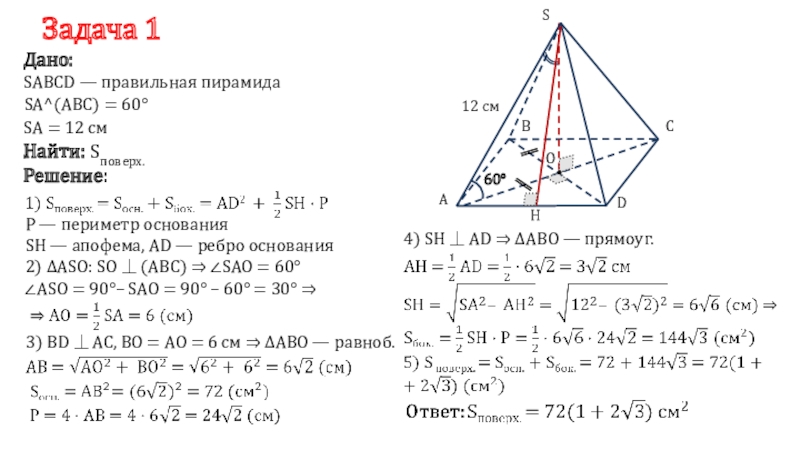
Слайд 7Задача 1
SABCD — правильная пирамида
Дано:
SA = 12 см
Решение:
SA^(ABC) = 60°
P — периметр основания
SH — апофема, AD — ребро основания
2)
∆ASO: SO ⏊ (ABC) ⇒ ∠SAO = 60°∠ASO = 90°– SAO = 90° – 60° = 30° ⇒
4) SH ⏊ AD ⇒ ∆ABO — прямоуг.
Найти: Sповерх.
3) BD ⏊ AC, BO = AO = 6 см ⇒ ∆ABO — равноб.
S
A
B
C
D
O
H
60°
12 см
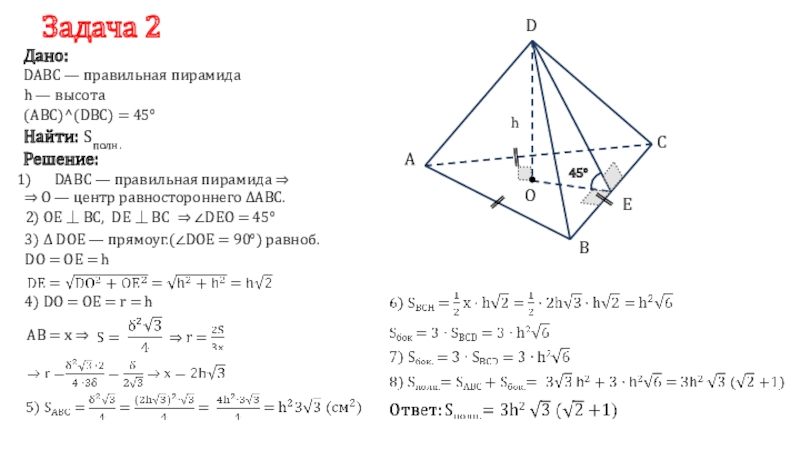
Слайд 8Задача 2
DABC — правильная пирамида
Дано:
(ABC)^(DBC) = 45°
Решение:
DABC — правильная пирамида
⇒
⇒ О — центр равностороннего ΔАВС.
h — высота
2) ОЕ
⏊ ВС, 3) Δ DOE — прямоуг.(∠DOE = 90°) равноб.
Найти: Sполн.
AB = x ⇒
4) DО = ОЕ = r = h
DO = OE = h
DE ⏊ BC
⇒ ∠DEO = 45°
A
B
C
D
O
h
45°
E
