Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
40. Компланарные вектора
Содержание
- 1. 40. Компланарные вектора
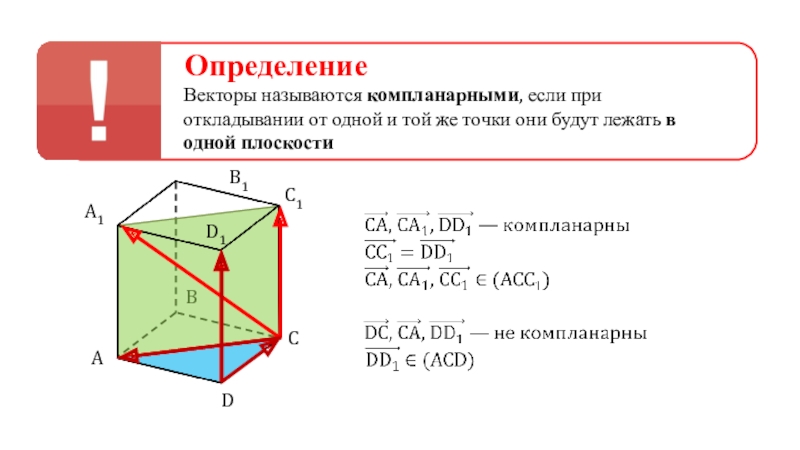
- 2. ОпределениеВекторы называются компланарными, если при откладывании от
- 3. — Любые два вектора компланарны— Три вектора,
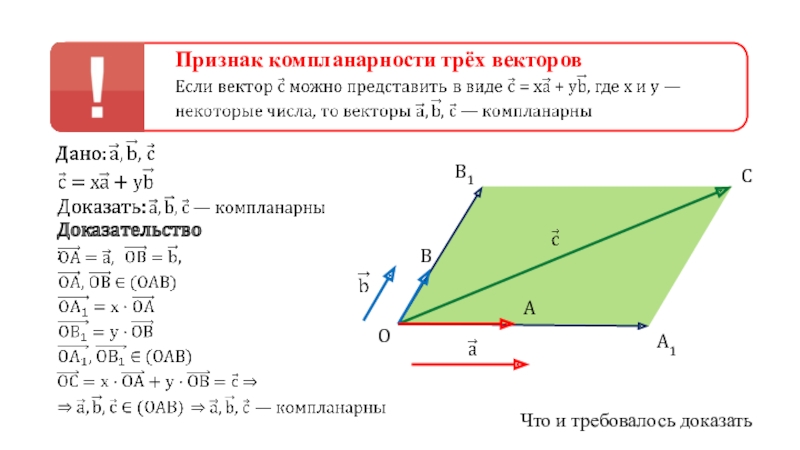
- 4. Признак компланарности трёх векторов Доказательство:B1CA1O AB Что и требовалось доказать
- 5. Утверждение, обратное признаку компланарности векторов:
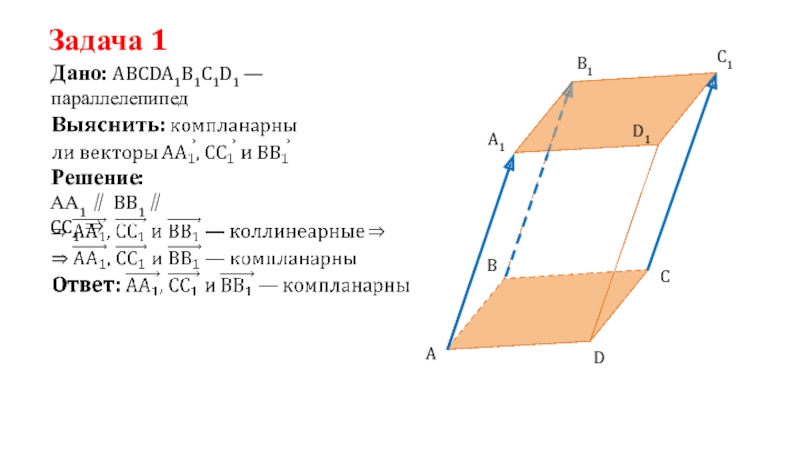
- 6. Задача 1Дано: ABCDA1B1C1D1 —параллелепипед Решение:АА1 ∥ BB1∥ CC1 ⇒ ADCBB1A1D1C1
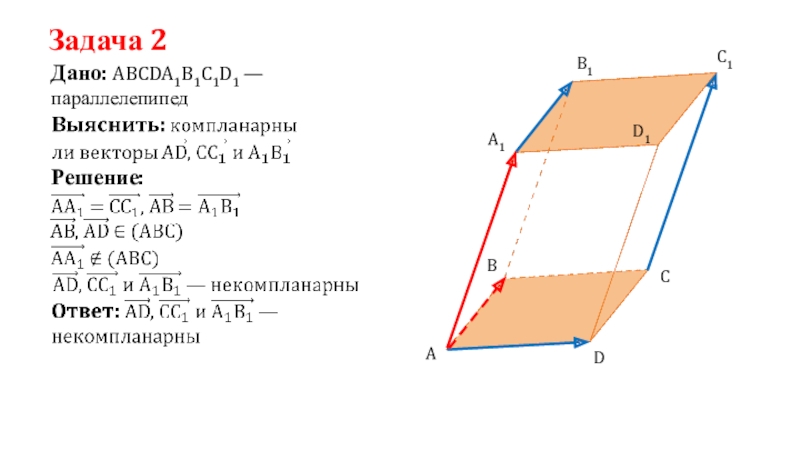
- 7. Задача 2Дано: ABCDA1B1C1D1 —параллелепипед Решение: ADCBB1A1D1C1
- 8. Скачать презентанцию
ОпределениеВекторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскостиCABDA1B1C1D1