Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
6. Трехмерное моделирование
Содержание
- 1. 6. Трехмерное моделирование
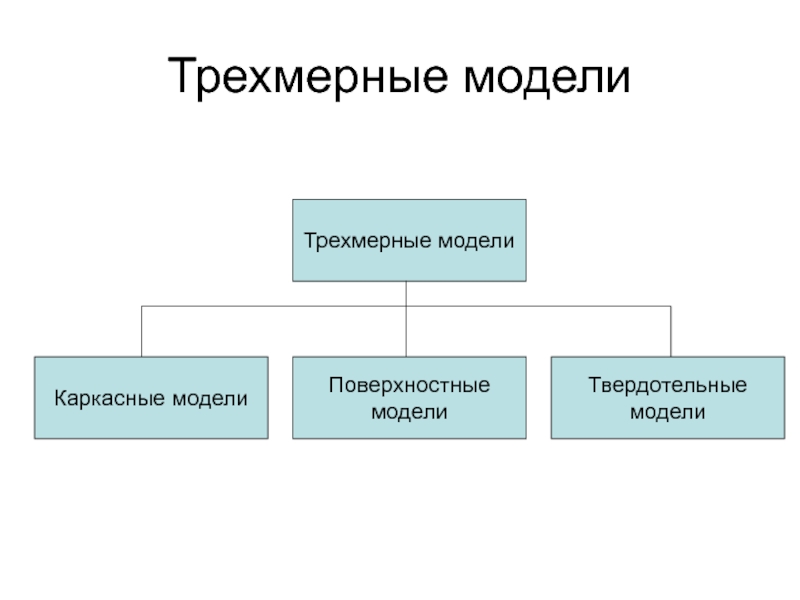
- 2. Трехмерные модели
- 3. Каркасные моделиГеометрический объект в каркасной модели представляется
- 4. Поверхностные моделиВ поверхностных моделях геометрический объект задается набором ограничивающих поверхностей.
- 5. Твердотельные моделиВ твердотельных моделях объект характеризуется границей
- 6. Аналитические моделиДля описания кривой на плоскости можно подобрать соответствующее аналитическое выражение.
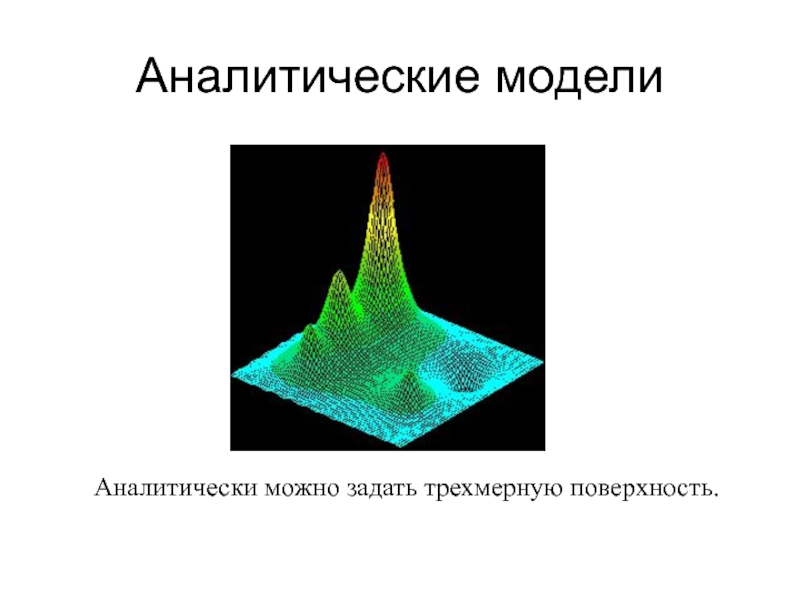
- 7. Аналитические моделиАналитически можно задать трехмерную поверхность.
- 8. Аналитические моделиПри аналитическом моделировании объектов часто используют
- 9. Аналитические модели
- 10. Аналитические моделиКубические кривыеx = X(t); y = Y(t); z = Z(t)
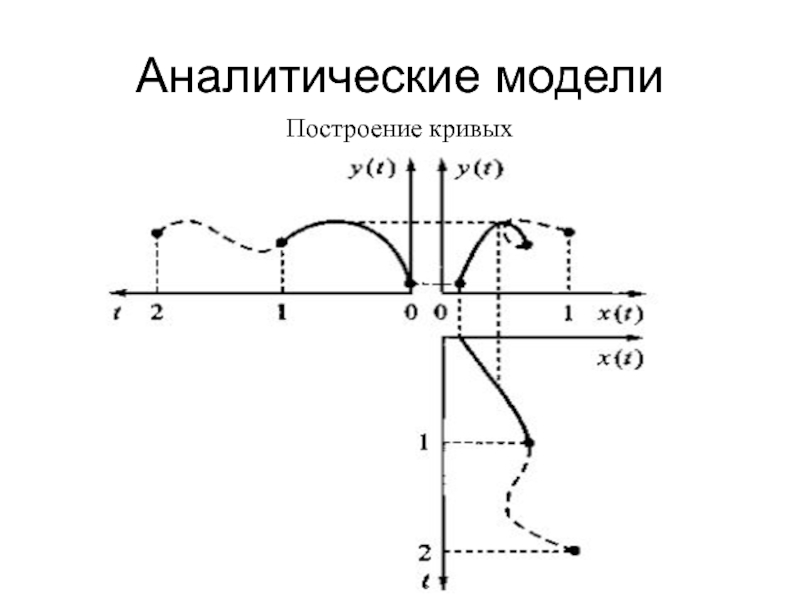
- 11. Аналитические моделиПостроение кривых
- 12. Аналитические моделиКубический полиномДля нахождения кубического полинома требуется
- 13. Аналитические моделиБазовая матрица, геометрический вектор, стыковочная матрицаQ(t)
- 14. Аналитические моделиКривые ЭрмитаКривые Эрмита – частный случай
- 15. Аналитические моделиБазовая матрица Эрмита
- 16. Аналитические моделиМатричное уравнение кривых ЭрмитаX(t) = TMGx,
- 17. Аналитические моделиКривые БезьеКривые Безье – специальный вид
- 18. Аналитические моделиПараметры кривых БезьеНачальный R1 и конечный
- 19. Аналитические моделиРасчет параметров кривых БезьеMh, Gh –
- 20. Аналитические моделиБазовая матрица кривых Безье
- 21. Аналитические моделиКубические B-сплайныB-сплайны – совокупность полиномиальных сегментов,
- 22. Аналитические моделиПример кубического B-сплайна
- 23. Аналитические моделиБазовая матрица кубического B-сплайна
- 24. Аналитические моделиБикубические поверхностиx = X(s, t); y
- 25. Аналитические моделиПоверхность произвольной формы разделяется на куски
- 26. Аналитические моделиКаждый участок бикубической поверхности задается шестнадцатью
- 27. Аналитические моделиТочки бикубической поверхности в форме Безье:(X,
- 28. Аналитические модели
- 29. Аналитические модели11Для сшивки двух кусков необходимо:совпадение смежных точекотсутствие излома в поперечном направлении
- 30. Полигональные моделиКривая на плоскости аппроксимируется набором отрезков,
- 31. Полигональные моделиВ этом случае поверхность аппроксимируется плоскими полигонами.
- 32. Полигональные моделиДля моделирования трехмерных объектом чаще всего
- 33. Полигональные моделиПолигоны описывается набором вершин – точек,
- 34. Аппроксимировать трехмерную плоскость можно с разной точностью.
- 35. Полигональные моделиПолигональная сетка – набор полигонов (граней),
- 36. Полигональные моделиПолигональная сетка задается списком полигонов и
- 37. Полигональные моделиСвойства полигональной сетки:Монолитность – сетка представляет
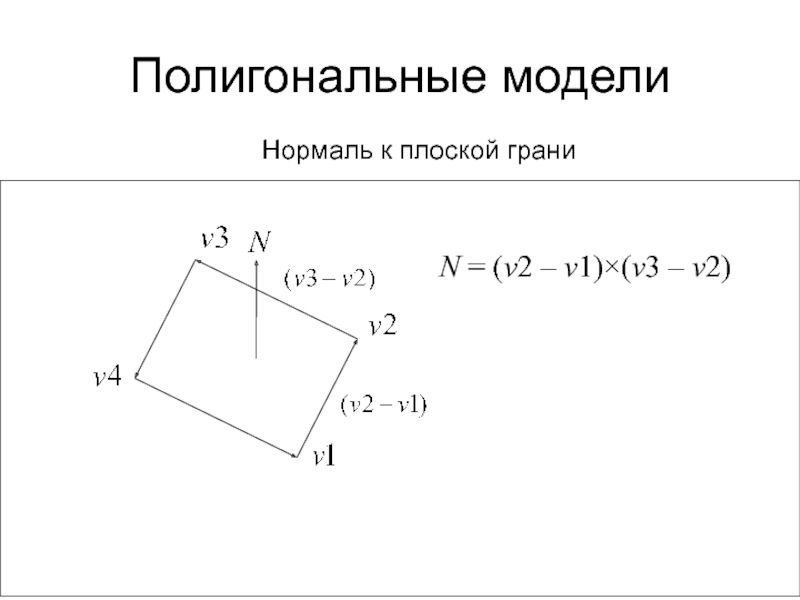
- 38. Полигональные моделиНормаль к плоской граниN = (v2 – v1)(v3 – v2)
- 39. Полигональные моделиМетод Ньюэлла
- 40. Полигональные моделиЕсли выполнять обход против часовой стрелки
- 41. Полигональные моделиV0 = (6, 1, 4), V1
- 42. Полигональные модели//грань 0glBegin(GL_POLYGON); glNormal3f(0.577, 0.577, 0.577); glVertex3f(1, 0, 0); glVertex3f(0,
- 43. Полигональные моделиСтруктура хранения данных полигональной сетки:в массиве
- 44. Полигональные модели
- 45. Полигональная модельПолиэдр – связная сетка из простых
- 46. Полигональные моделиФундаментальное соотношение между количеством граней F,
- 47. Полигональные моделиЕсли все грани полиэдра одинаковы и
- 48. Скачать презентанцию
Слайды и текст этой презентации
Слайд 3Каркасные модели
Геометрический объект в каркасной модели представляется набором ребер. В
качестве ребер выступают отрезки, кривые различных порядков, сплайны и др.
Слайд 4Поверхностные модели
В поверхностных моделях геометрический объект задается набором ограничивающих поверхностей.
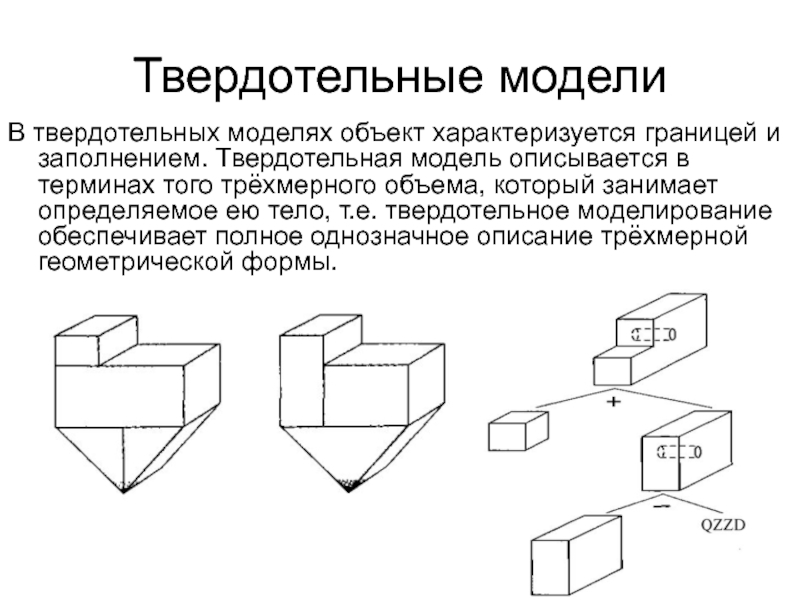
Слайд 5Твердотельные модели
В твердотельных моделях объект характеризуется границей и заполнением. Твердотельная
модель описывается в терминах того трёхмерного объема, который занимает определяемое
ею тело, т.е. твердотельное моделирование обеспечивает полное однозначное описание трёхмерной геометрической формы.Слайд 6Аналитические модели
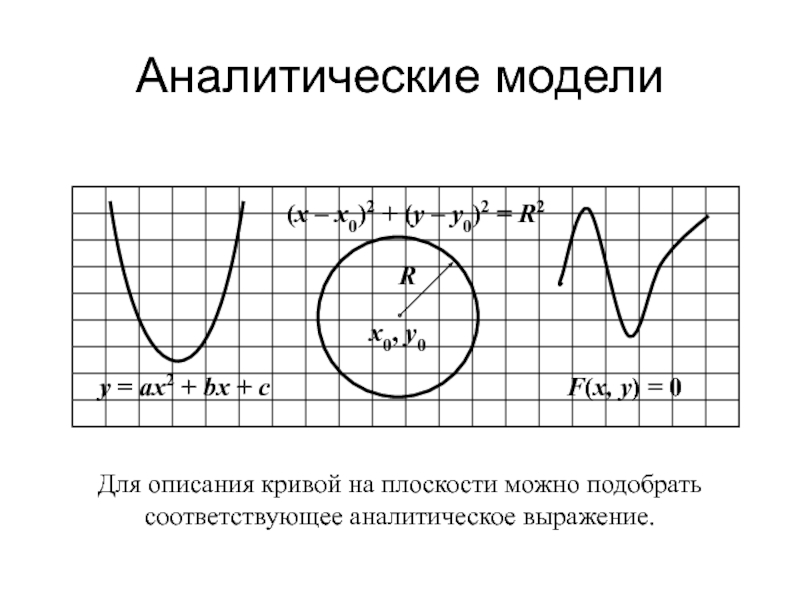
Для описания кривой на плоскости можно подобрать соответствующее аналитическое
выражение.
Слайд 8Аналитические модели
При аналитическом моделировании объектов часто используют поверхности второго порядка:
Ax2
+ By2 + Cz2 + Dxy + Exz + Fyz
+ Gx + Hy + Jz + K = 0Слайд 12Аналитические модели
Кубический полином
Для нахождения кубического полинома требуется установить значения его
четырех коэффициентов. Для этого следует наложить на кривую четыре дополнительных
условия. Такими условиями служат значения кубического сегмента на концевых точках, значения касательного вектора и условия связности между соседними сегментами.Касательный вектор:
Слайд 13Аналитические модели
Базовая матрица, геометрический вектор, стыковочная матрица
Q(t) = TC =
TMG = BG
M – базовая матрица четвертого порядка
G – геометрический
вектор (G = [G1 G2 G3 G4]T)B – стыковочная матрица (B = TM)
Слайд 14Аналитические модели
Кривые Эрмита
Кривые Эрмита – частный случай кубических полиномиальных кривых,
которые задаются концевыми точками P1, P4 и касательными векторами R1,
R4 в них.Слайд 16Аналитические модели
Матричное уравнение кривых Эрмита
X(t) = TMGx, Y(t) = TMGy,
Z(t) = TMGz
Q(t) = TMG
G = [P1 P4 R1 R4]T
Слайд 17Аналитические модели
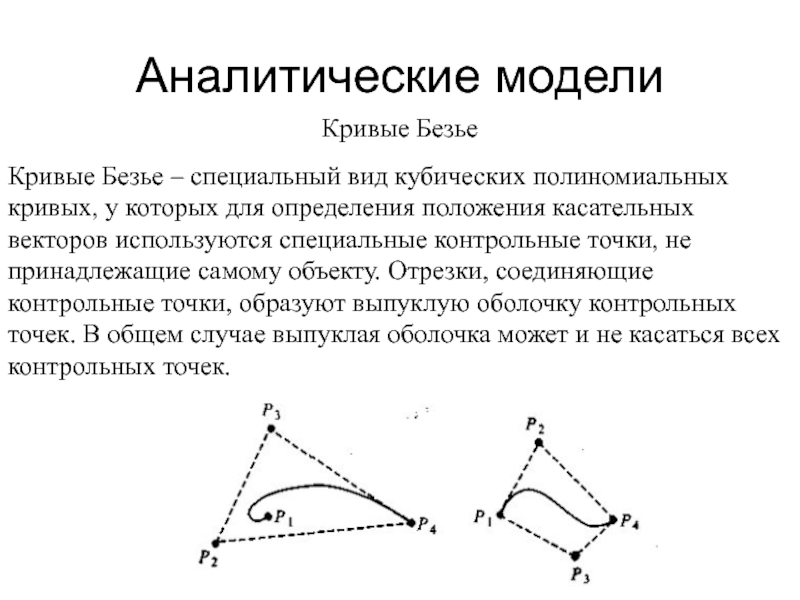
Кривые Безье
Кривые Безье – специальный вид кубических полиномиальных кривых,
у которых для определения положения касательных векторов используются специальные контрольные
точки, не принадлежащие самому объекту. Отрезки, соединяющие контрольные точки, образуют выпуклую оболочку контрольных точек. В общем случае выпуклая оболочка может и не касаться всех контрольных точек.Слайд 18Аналитические модели
Параметры кривых Безье
Начальный R1 и конечный R4 касательные векторы
кривой Безье зависят от радиус-векторов P1, P2, P3 и P4,
соединяющих контрольные точки с началом координат:Слайд 19Аналитические модели
Расчет параметров кривых Безье
Mh, Gh – базовая матрица и
геометрический вектор Эрмита
Mb, Gb – базовая матрица и геометрический вектор
БезьеMb – матрица преобразования геометрических векторов
Слайд 21Аналитические модели
Кубические B-сплайны
B-сплайны – совокупность полиномиальных сегментов, положение которых задается
контрольными точками. Кубический B-сплайн задается последовательностью полиномиальных сегментов Q3, Q4,
…, Qm, положение которых зависит от контрольных точек P0, P1, …, Pm (m 3). Сегменты определяются на интервалах ti t < ti+1, 3 i < m, t3 = 0, ti+1 – ti = 1.Геометрический вектор i-го сегмента:
Слайд 24Аналитические модели
Бикубические поверхности
x = X(s, t); y = Y(s, t);
z = Z(s, t)
A(s, t) = a11s3t3 + a12s3t2 +
a13s3t + a14s3 + a21s2t3 + a22s2t2 + a23s2t + a14s2 + a31st3 + a32st2 + a33st + a44s + a41t3 + a42t2 + a43t + a44Слайд 25Аналитические модели
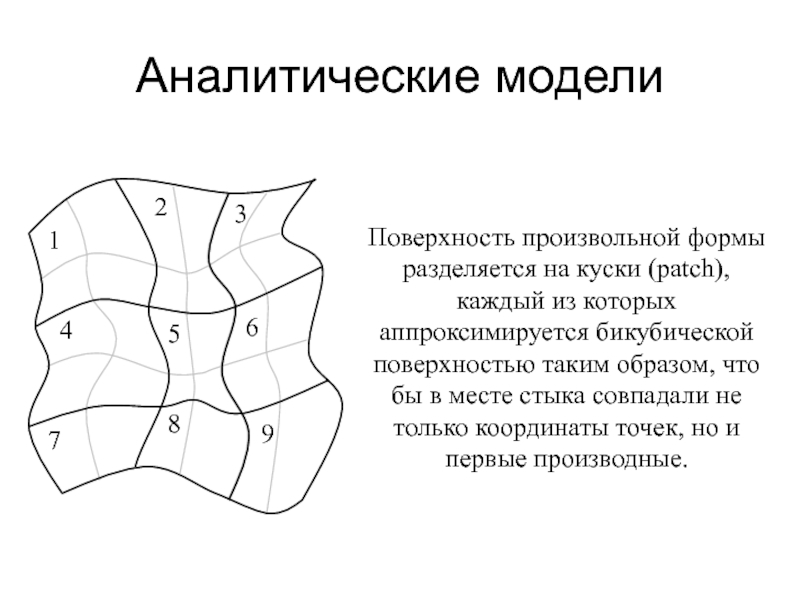
Поверхность произвольной формы разделяется на куски (patch), каждый из
которых аппроксимируется бикубической поверхностью таким образом, что бы в месте
стыка совпадали не только координаты точек, но и первые производные.Слайд 26Аналитические модели
Каждый участок бикубической поверхности задается шестнадцатью точками. Тогда бикубическая
поверхность в форме Безье задается в следующем виде:
X(s, t)
= SMbGbxMbTTT
Y(s, t) = SMbGbyMbTTT
Z(s, t) = SMbGbzMbTTTили в форме B-сплайна
X(s, t) = SMsGsxMsTTT
Y(s, t) = SMsGsyMsTTT
Z(s, t) = SMsGszMsTTT
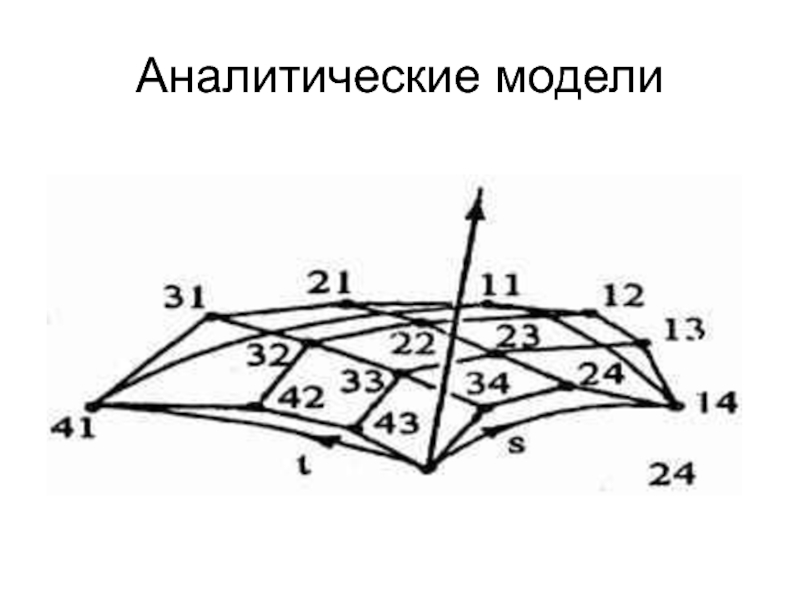
Слайд 27Аналитические модели
Точки бикубической поверхности в форме Безье:
(X, Y, Z)11, (X,
Y, Z)14, (X, Y, Z)41, (X, Y, Z)44 – координаты
четырех угловых точек;(X, Y, Z)21, (X, Y, Z)22, (X, Y, Z)12;
(X, Y, Z)13, (X, Y, Z)23, (X, Y, Z)24;
(X, Y, Z)43, (X, Y, Z)33, (X, Y, Z)34;
(X, Y, Z)42, (X, Y, Z)32, (X, Y, Z)31 – концы касательных векторов.
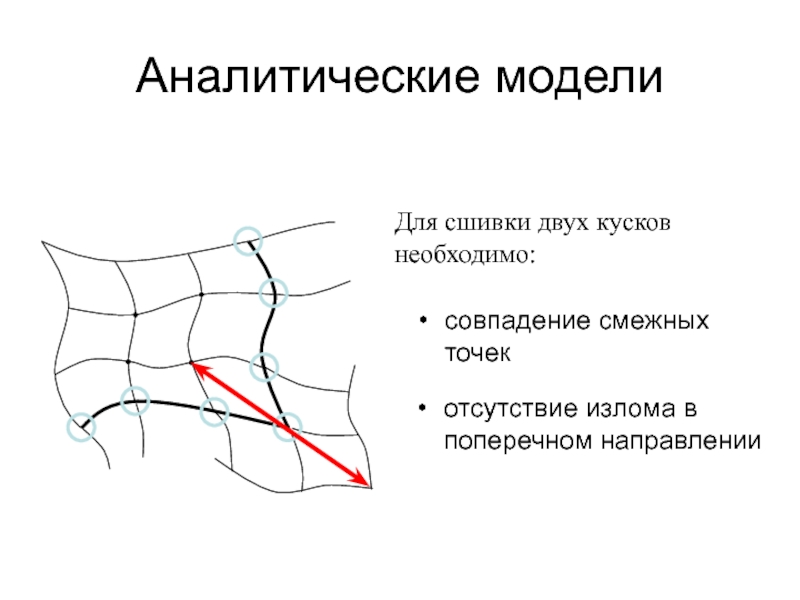
Слайд 29Аналитические модели
11
Для сшивки двух кусков необходимо:
совпадение смежных
точек
отсутствие излома в поперечном
направлении
Слайд 30Полигональные модели
Кривая на плоскости аппроксимируется набором отрезков, каждый из которых
определяется двумя точками – начала и конца
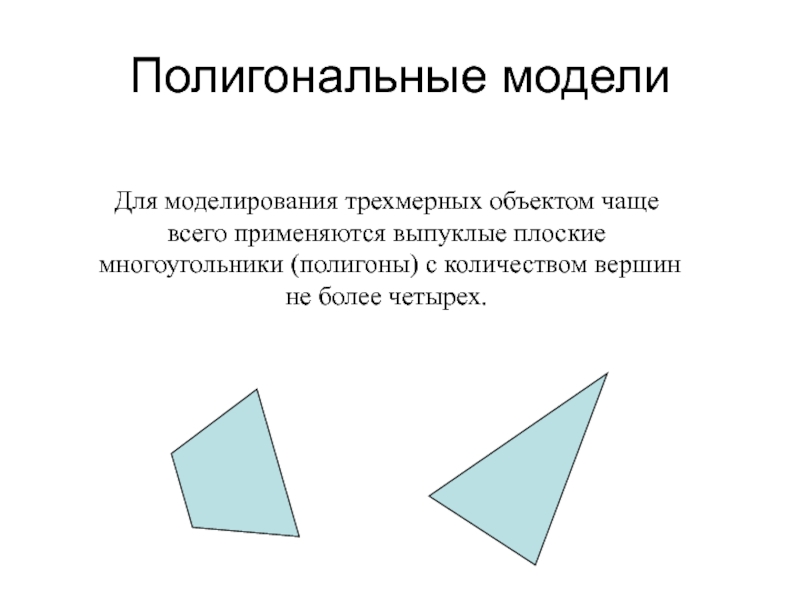
Слайд 32Полигональные модели
Для моделирования трехмерных объектом чаще всего применяются выпуклые плоские
многоугольники (полигоны) с количеством вершин не более четырех.
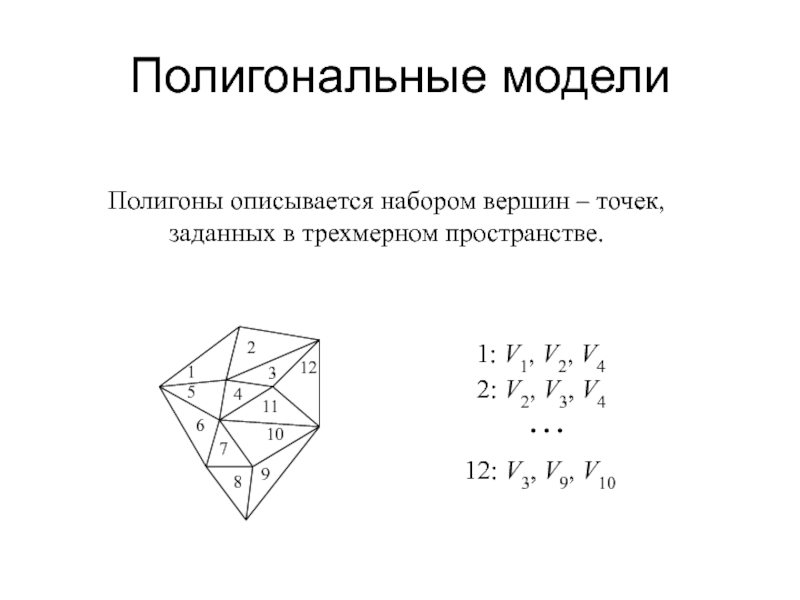
Слайд 33Полигональные модели
Полигоны описывается набором вершин – точек, заданных в трехмерном
пространстве.
1: V1, V2, V4
2: V2, V3, V4
. . .
12:
V3, V9, V10Слайд 34Аппроксимировать трехмерную плоскость можно с разной точностью. Количество вершин в
модели зависит от требуемого качества картинки и от ожидаемой скорости
рендеринга - чем больше вершин, тем выше качество и тем медленнее рендеринг.Полигональные модели
Слайд 35Полигональные модели
Полигональная сетка – набор полигонов (граней), которые в совокупности
образуют форму объекта.
Полигональная сетка является практически во всех графических системах
стандартным способом представления широкого класса объемных форм.Слайд 36Полигональные модели
Полигональная сетка задается списком полигонов и информацией о направлении,
куда обращен каждый полигон.
Информация о направлении задается в виде нормали к
плоскости грани.Нормаль указывает внешнее направление от объекта.
Слайд 37Полигональные модели
Свойства полигональной сетки:
Монолитность – сетка представляет монолитный объект, если
совокупность его граней заключает в себе некоторое конечное пространство;
Связность –
сетка называется связной, если между любыми двумя вершинами существует непрерывный путь вдоль ребер полигона (если сетка не является связной, то обычно она представляет более одного объекта);Простота – сетка называется простой, если отображаемый ею объект является монолитным и не содержит отверстий (это означает, что объект может быть деформирован в сферу, не подвергаясь разрезанию);
Плоскостность – сетка называется плоской, если каждая грань представляемого ею объекта является плоским полигоном, т.е. вершины каждой грани лежат в одной плоскости;
Выпуклость – сетка представляет выпуклый объект, если прямая, соединяющая любые две точки внутри этого объекта, целиком лежит внутри него.
Слайд 40Полигональные модели
Если выполнять обход против часовой стрелки с наружной стороны
грани, то полученный вектор показывает направление наружу от грани.
Слайд 42Полигональные модели
//грань 0
glBegin(GL_POLYGON);
glNormal3f(0.577, 0.577, 0.577);
glVertex3f(1, 0, 0);
glVertex3f(0, 1, 0);
glVertex3f(0, 0,
1);
glEnd();
//грань 1
glBegin(GL_POLYGON);
glNormal3f(0, 0, -1);
glVertex3f(0, 0, 0);
glVertex3f(0, 1, 0);
glVertex3f(1, 0, 0);
glEnd();
//грань
2glBegin(GL_POLYGON);
glNormal3f(-1, 0, 0);
glVertex3f(0, 0, 0);
glVertex3f(0, 0, 1);
glVertex3f(0, 1, 0);
glEnd();
//грань 3
glBegin(GL_POLYGON);
glNormal3f(0, -1, 0);
glVertex3f(1, 0, 0);
glVertex3f(0, 0, 1);
glVertex3f(0, 0, 0);
glEnd();
Описание тетраэдра в OpenGL
Слайд 43Полигональные модели
Структура хранения данных полигональной сетки:
в массиве вершин хранятся без
повторений координаты всех вершин;
в массиве нормалей хранятся без повторений компоненты
нормалей к каждой грани;в массиве граней для каждой грани хранятся индексы вершин из массива вершин и индексы нормалей, ассоциированных с каждой вершиной грани.
Слайд 45Полигональная модель
Полиэдр – связная сетка из простых плоских полигонов, которая
ограничивает конечный объем пространства.
Каждое ребро полиэдра принадлежит ровно двум граням;
В
каждой вершине полиэдра встречается не менее трех ребер;Грани полиэдра не являются взаимопроникающими: две грани не имеют общих точек или пересекаются только вдоль их общего ребра.
Слайд 46Полигональные модели
Фундаментальное соотношение между количеством граней F, ребер E и
вершин V простого многогранника устанавливает формула Эйлера:
V + F –
E = 2.Обощение этой формулы на непростой полиэдр имеет вид:
V + F – E = 2 + H – 2G,
где H – общее число отверстий, имеющихся в гранях, G – число отверстий в самом полиэдре.
Слайд 47Полигональные модели
Если все грани полиэдра одинаковы и каждая из них
является правильным многоугольником, то объект называется правильным многогранником. Существует всего
пять таких объектов, которые называют платоновыми телами:Тетраэдр: V = 4, F = 4, E = 6, грани – треугольники;
Гексаэдр: V = 8, F = 6, E = 12, грани – квадраты;
Октаэдр: V = 6, F = 8, E = 12, грани – треугольники;
Икосаэдр: V = 12, F = 20, E = 30, грани – треугольники;
Додекаэдр: V = 20, F = 12, E = 30, грани – пятиугольники.
Нормальный вектор к каждой грани платонового тела – это вектор из начала координат к центру грани, представляющему собой среднее значение вершин.