Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
7. Алгоритмизация и программирование
Содержание
- 1. 7. Алгоритмизация и программирование
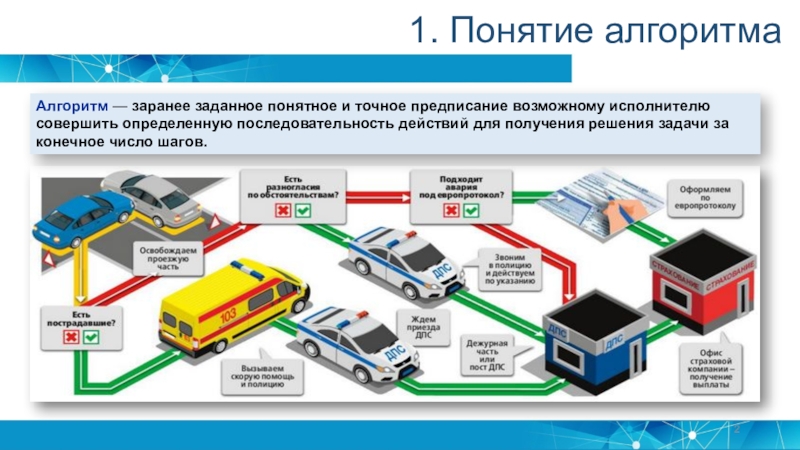
- 2. 1. Понятие алгоритмаАлгоритм — заранее заданное понятное
- 3. Алгоритм – это точно определенное описание способа
- 4. Программа – упорядоченная последовательность команд, необходимых для
- 5. Языки программирования – это искусственные языки с
- 6. При нарушении формы записи программы возникают синтаксические
- 7. С помощью языков программирования создается текст программы.
- 8. Компиляторы же полностью обрабатывают текст программы, просматривают
- 9. Этапы решения задач с помощью компьютераРешение задач
- 10. Этапы решения задач с помощью компьютера2. Анализ и
- 11. Этапы решения задач с помощью компьютера4. Пpогpаммиpование: выбор
- 12. Этапы решения задач с помощью компьютера6. Анализ результатов
- 13. 2. Свойства алгоритмаПонятность для исполнителя — исполнитель
- 14. 3. Формы записи алгоритмаСловесная (запись на естественном
- 15. Словесная форма записи алгоритмаАлгоритм в данной форме
- 16. Является более компактной и наглядной по сравнению
- 17. Графическая форма записи алгоритма
- 18. ПсевдокодПсевдокод представляет собой систему обозначений и правил,
- 19. ПсевдокодПримеры записи алгоритмов:алг Сумма квадратов (арг цел
- 20. Программная форма записиПримеры программной записи алгоритмовfunction sortBubble(data)
- 21. Правила составления схемы алгоритмаКаждый блок имеет один
- 22. 4. Базовые алгоритмические структурыАлгоритмические структуры — типовые группы элементарных шагов алгоритма. Алгоритмические структурыЛинейныеВетвленияЦиклическиеРекурсивныеВспомогательныеБазовые
- 23. Линейная структураЛинейный алгоритм P (или его часть)
- 24. Алгоритмы линейной структурыПример 1.Требуется вычислить площадь поперечного
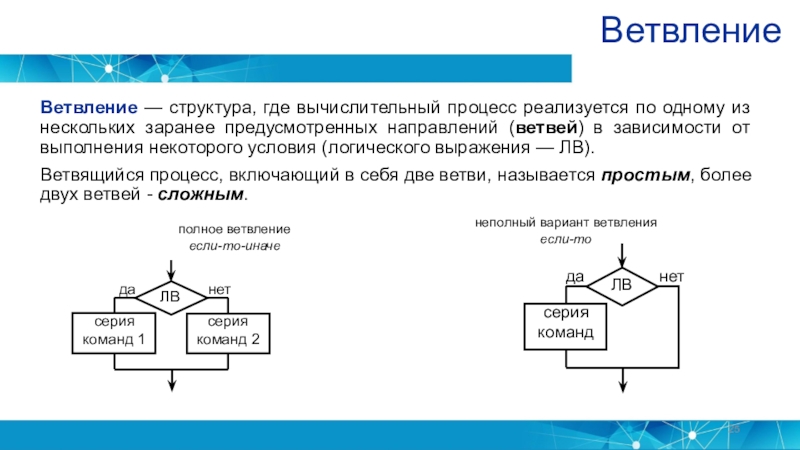
- 25. ВетвлениеВетвление — структура, где вычислительный процесс реализуется
- 26. Алгоритмы разветвляющейся структурыПример 2. Составить схему алгоритма
- 27. Алгоритмы разветвляющейся структуры x + a
- 28. Алгоритмы разветвляющейся структурыПример 4. Даны различные x,
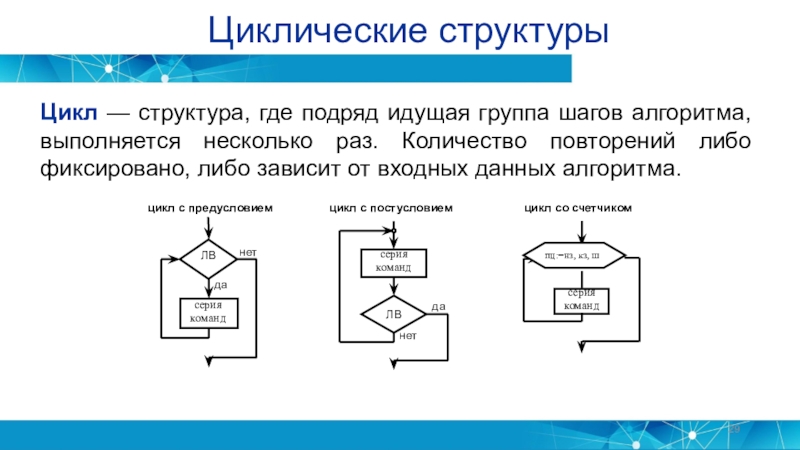
- 29. Циклические структурыЦикл — структура, где подряд идущая
- 30. Алгоритмы циклической структуры
- 31. Алгоритмы циклической структуры
- 32. Переменные и константыРеальные данные, с которыми работает
- 33. 6. Уровень языка программированияКлассификация языков программирования по
- 34. В зависимости от детализации предписаний определяют уровень
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 17. Алгоритмизация
и программирование
1. Понятие алгоритма
2. Свойства алгоритма
3. Формы записи
алгоритмов
Слайд 21. Понятие алгоритма
Алгоритм — заранее заданное понятное и точное предписание
возможному исполнителю совершить определенную последовательность действий для получения решения задачи
за конечное число шагов.Слайд 3Алгоритм – это точно определенное описание способа решения задачи в
виде конечной последовательности действий.
Для представления алгоритма в виде, понятном
ПК, служат языки программирования, с помощью которых пишется программа. Затем программа с помощью транслятора либо переводится в машинный код, либо исполняется. Слайд 4Программа – упорядоченная последовательность команд, необходимых для управления компьютером (ПК).
Эти команды поступают на процессор как совокупность нулей и единиц,
т.е. числами. Последовательность чисел – машинный код. Слайд 5Языки программирования – это искусственные языки с ограниченным числом слов,
значения которых понятно транслятору, и очень строгими правилами записи команд
(операторов).Слайд 6При нарушении формы записи программы возникают синтаксические либо логические ошибки.
Поиск ошибок – тестирование, процесс устранения ошибок – отладка.
Слайд 7С помощью языков программирования создается текст программы. Чтобы получить работающую
программу необходимо либо сразу перевести текст программы в машинный код
(откомпилировать), либо сразу выполнять команды языка с помощью интерпретатора, который поочередно анализирует отдельные команды и затем сразу же выполняет их. После того как текущий оператор выполнен, интерпретатор перейдет к следующему. Такие программы работают медленно и не могут выполняться сами, отдельно от интерпретатора.Слайд 8Компиляторы же полностью обрабатывают текст программы, просматривают его в поисках
синтаксических ошибок и автоматически переводят его в машинный код. В
результате получается компактная, быстрая «исполняемая» программа. Однако компиляторы неэффективны при работе с данными сложной структуры.Слайд 9Этапы решения задач с помощью компьютера
Решение задач с помощью компьютера
включает в себя следующие основные этапы, часть из которых осуществляется
без участия компьютера.Постановка задачи:
сбоp инфоpмации о задаче;
фоpмулиpовка условия задачи;
опpеделение конечных целей pешения задачи;
определение формы выдачи результатов;
описание данных (их типов, диапазонов величин, структуры и т.п. ).
Слайд 10Этапы решения задач с помощью компьютера
2. Анализ и исследование задачи, модели:
анализ существующих аналогов;
анализ технических и программных средств;
pазpаботка математической
модели; разработка структур данных.
3. Разработка алгоритма:
выбор метода проектирования алгоритма;
выбор формы записи алгоритма (блок-схемы, псевдокод и др.);
выбор тестов и метода тестирования;
проектирование алгоритма.
Слайд 11Этапы решения задач с помощью компьютера
4. Пpогpаммиpование:
выбор языка программирования;
уточнение
способов организации данных;
запись алгоpитма на выбpанном языке пpогpаммиpования.
5. Тестиpование
и отладка: синтаксическая отладка;
отладка семантики и логической стpуктуpы;
тестовые pасчеты и анализ pезультатов тестиpования;
совершенствование пpогpаммы.
Отладка программы — это процесс поиска и устранения ошибок в программе, производимый по результатам её прогона на компьютере.
Тестирование (англ. test — испытание) — это испытание, проверка правильности работы программы в целом, либо её составных частей.
Слайд 12Этапы решения задач с помощью компьютера
6. Анализ результатов решения задачи и
уточнение в случае необходимости математической модели с повторным выполнением этапов
2 — 5.7. Сопровождение программы: это работы, связанные с обслуживанием программ в процессе их эксплуатации
доработка программы для решения конкретных задач;
составление документации к pешенной задаче, к математической модели, к алгоpитму, к пpогpамме, к набору тестов, к использованию.
Слайд 132. Свойства алгоритма
Понятность для исполнителя — исполнитель алгоритма должен понимать,
как его выполнять.
Дискретность (прерывность, раздельность) — алгоритм должен представлять
решение задачи как последовательное выполнение простых (или ранее определённых) шагов (этапов).Определённость — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола.
Результативность (или конечность) — за конечное число шагов алгоритм либо должен приводить к решению задачи, либо останавливаться из-за невозможности получить решение с выдачей соответствующего сообщения, либо неограниченно продолжаться в течение заданного времени с выдачей промежуточных результатов.
Массовость — алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для класса задач, различающихся лишь исходными данными.
Слайд 143. Формы записи алгоритма
Словесная (запись на естественном языке);
Графическая (изображения из
графических символов);
Псевдокоды (полуформализованные описания алгоритмов на условном алгоритмическом языке, включающие
в себя как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.);Программная (тексты на языках программирования).
Слайд 15Словесная форма записи алгоритма
Алгоритм в данной форме записи представляет собой
последовательность действий:
задать два числа;
если числа равны, то взять любое из
них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;определить большее из чисел;
заменить большее из чисел разностью большего и меньшего из чисел;
повторить алгоритм с шага 2.
Недостатки словесного способа:
строго не формализуем для машинного исполнения;
избыточность;
допускают неоднозначность толкования отдельных предписаний.
Слайд 16Является более компактной и наглядной по сравнению со словесным;
Изображается в
виде последовательности связанных между собой функциональных блоков, каждый из которых
соответствует выполнению одного или нескольких действий;Такое графическое представление называется схемой алгоритма или блок-схемой.
Графическая форма записи алгоритма
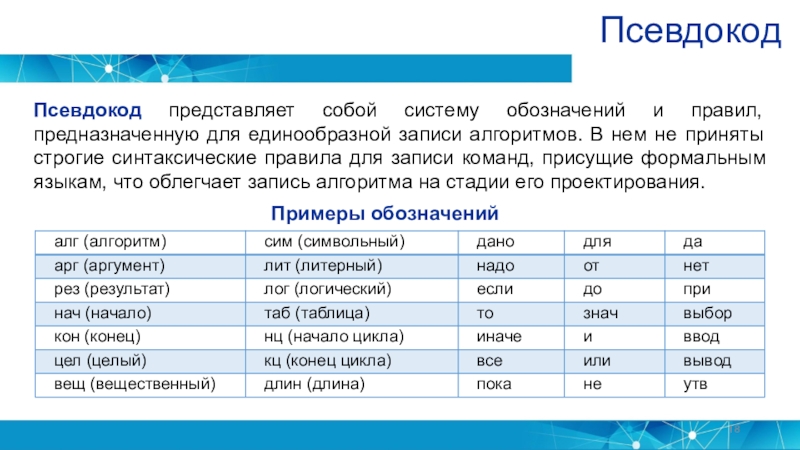
Слайд 18Псевдокод
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной
записи алгоритмов. В нем не приняты строгие синтаксические правила для
записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования.Примеры обозначений
Слайд 19Псевдокод
Примеры записи алгоритмов:
алг Сумма квадратов (арг цел n, рез цел
S)
дано | n > 0
надо | S = 1*1 +
2*2 + 3*3 + ... + n*nнач цел i
ввод n; S = 0
нц для i от 1 до n
S = S + i*i
кц
вывод "S = ", S
кон
Слайд 20Программная форма записи
Примеры программной записи алгоритмов
function sortBubble(data) {
var
tmp;
for (var i = data.length - 1;
i > 0; i--) { var counter=0;
for (var j = 0; j < i; j++) {
if (data[j] > data[j+1]) {
tmp = data[j]; data[j] = data[j+1];
data[j+1] = tmp; counter++;
}
}
if(counter==0){ break; }
}
return data;
};
void bubble(int* a, int n) {
for (int i = n - 1; i >= 0; i--) {
for (int j = 0; j < i; j++) {
if (a[j] > a[j + 1]) {
int tmp = a[j];
a[j] = a[j + 1];
a[j + 1] = tmp;
}
}
}
}
JavaScript
C++
Слайд 21Правила составления схемы алгоритма
Каждый блок имеет один или несколько входов,
кроме блока "НАЧАЛО", который не имеет входа вообще. Несколько стрелок,
идущих на вход некоторого блока, положено соединять до точки входа в блок.Каждый блок имеет строго один выход, кроме блока "КОНЕЦ", который не имеет выхода, и блока проверки условия, имеющего два выхода. Блок проверки условия обозначает разветвление вычислительного процесса в зависимости от выполнения некоторого условия. Чтобы различить выходы этого блока, их помечают словами "да" и "нет". Если условие, записанное в блоке, выполняется, то вычислительный процесс пойдет по стрелке со словом "да", иначе - по стрелке со словом "нет’’.
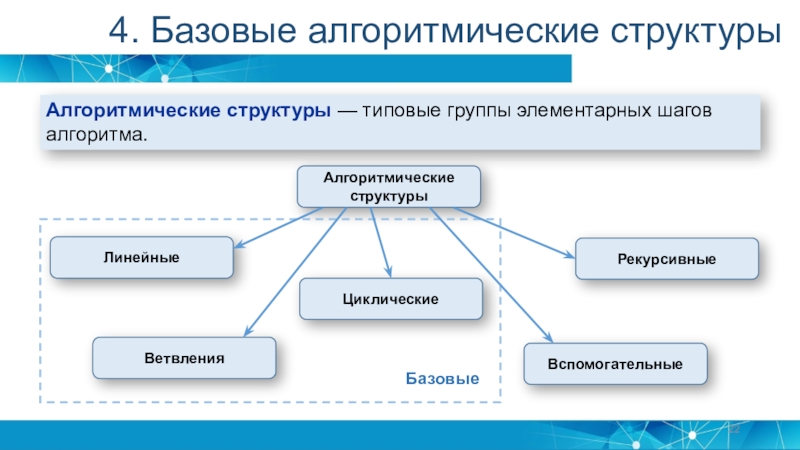
Слайд 224. Базовые алгоритмические структуры
Алгоритмические структуры — типовые группы элементарных шагов
алгоритма.
Алгоритмические структуры
Линейные
Ветвления
Циклические
Рекурсивные
Вспомогательные
Базовые
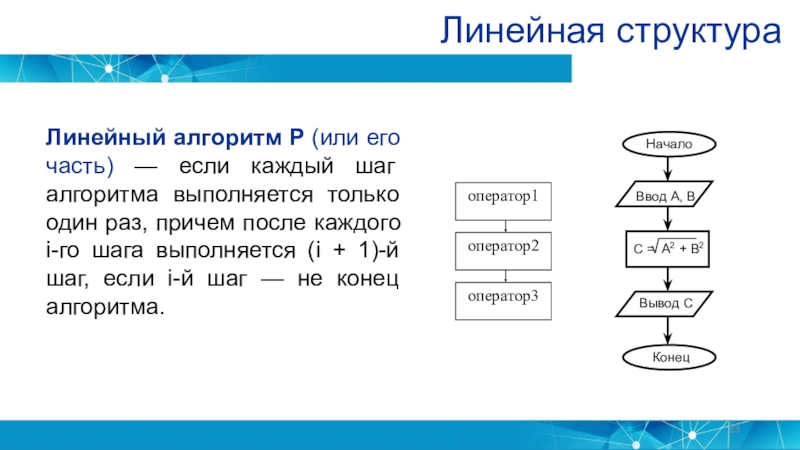
Слайд 23Линейная структура
Линейный алгоритм P (или его часть) — если каждый
шаг алгоритма выполняется только один раз, причем после каждого i-го
шага выполняется (i + 1)-й шаг, если i-й шаг — не конец алгоритма.Слайд 24Алгоритмы линейной структуры
Пример 1.Требуется вычислить площадь поперечного сечения ствола по
формуле эллипса g=·D· d/4, где D - наибольший диаметр сечения ствола,
d - наименьший диаметр сечения ствола, число =3.1416.Переменной называется величина, значение которой может меняться в процессе работы алгоритма. Каждой переменной отводится определённое место в памяти ЭВМ (ячейка памяти). В эту ячейку помещается текущее значение переменной. Вновь вычисленное значение переменной пересылается в ту же ячейку. При этом "старое содержимое" ячейки теряется.
Можно записать схему алгоритма так
начало
ввод D,d,
g=· D· d/4
вывод g
конец
Слайд 25Ветвление
Ветвление — структура, где вычислительный процесс реализуется по одному из
нескольких заранее предусмотренных направлений (ветвей) в зависимости от выполнения некоторого
условия (логического выражения — ЛВ).Ветвящийся процесс, включающий в себя две ветви, называется простым, более двух ветвей - сложным.
полное ветвление
если-то-иначе
неполный вариант ветвления
если-то
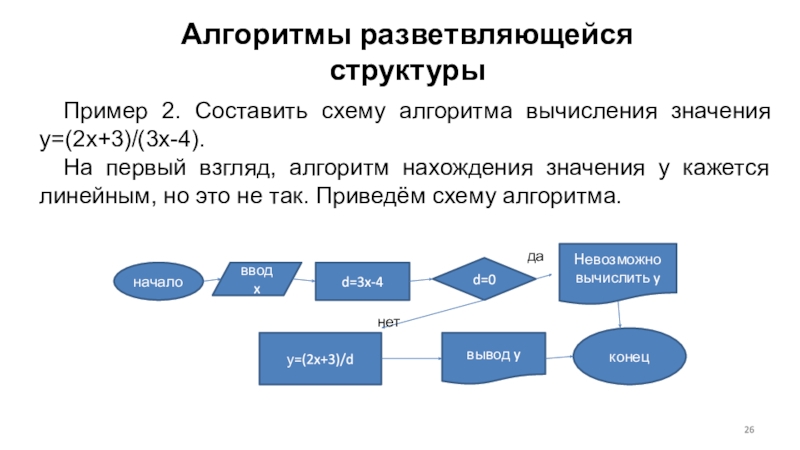
Слайд 26Алгоритмы разветвляющейся структуры
Пример 2. Составить схему алгоритма вычисления значения y=(2x+3)/(3x-4).
На
первый взгляд, алгоритм нахождения значения y кажется линейным, но это
не так. Приведём схему алгоритма.начало
ввод x
d=3x-4
d=0
у=(2x+3)/d
вывод y
конец
да
нет
Невозможно вычислить y
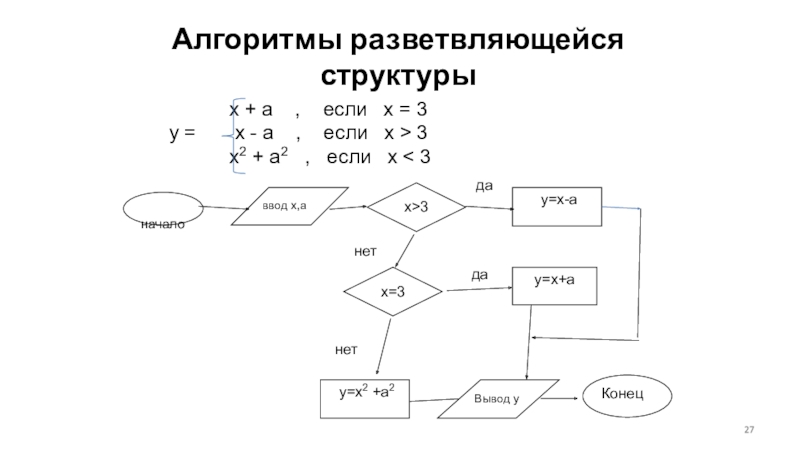
Слайд 27Алгоритмы разветвляющейся структуры
x + a , если
x = 3
y = x - a
, если x > 3x2 + a2 , если x < 3
начало
ввод x,a
y=x+a
x>3
y=x-a
y=x2 +a2
Вывод y
Конец
x=3
да
да
нет
нет
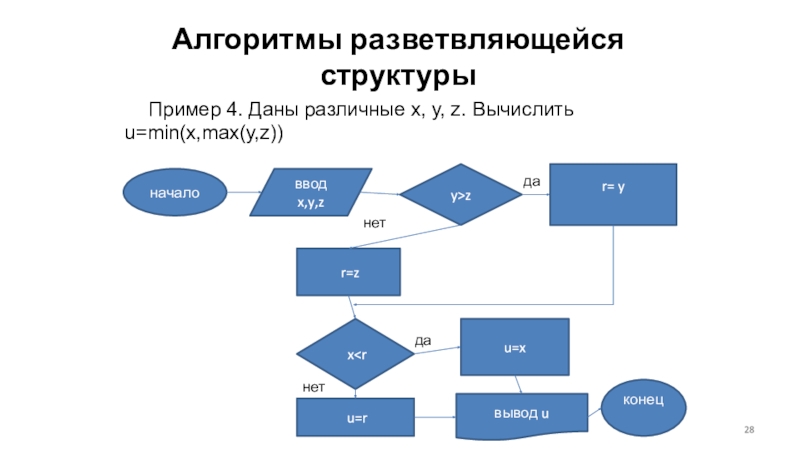
Слайд 28Алгоритмы разветвляющейся структуры
Пример 4. Даны различные x, y, z. Вычислить
u=min(x,max(y,z))
начало
ввод x,y,z
y>z
r= y
r=z
x u=r u=x вывод u конец да нет да нет
Слайд 29Циклические структуры
Цикл — структура, где подряд идущая группа шагов алгоритма,
выполняется несколько раз. Количество повторений либо фиксировано, либо зависит от
входных данных алгоритма.Слайд 30Алгоритмы циклической структуры
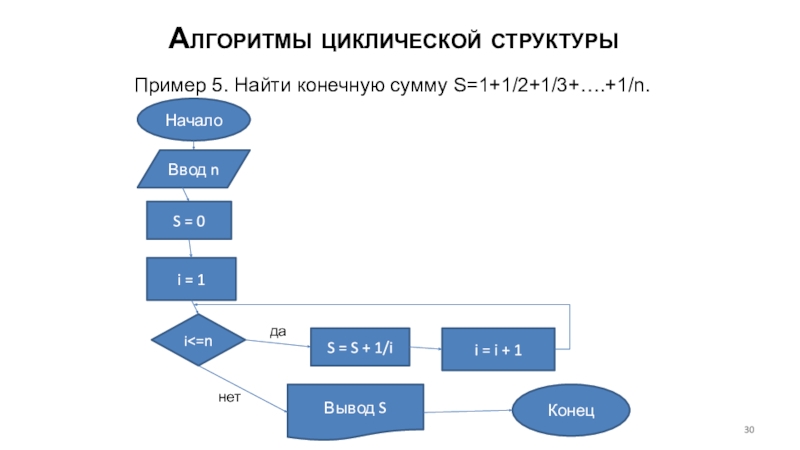
Пример 5. Найти конечную сумму S=1+1/2+1/3+….+1/n.
Начало
Ввод n
S = 0
i = 1
i<=n
Вывод S
Конец
S = S + 1/i
i = i + 1
да
нет
Слайд 31Алгоритмы циклической структуры
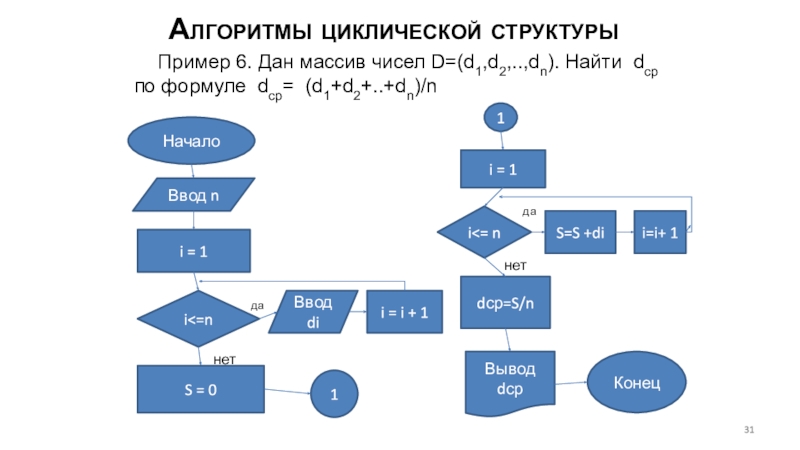
Пример 6. Дан массив чисел D=(d1,d2,..,dn). Найти dср по формуле dср= (d1+d2+..+dn)/n
Начало
Ввод n
i = 1
i<=n
S = 0
1
1
i = i + 1
i = 1
i<= n
dср=S/n
S=S +di
i=i+ 1
Вывод dср
Конец
Ввод di
да
да
нет
нет
Слайд 32Переменные и константы
Реальные данные, с которыми работает программа, - это:
числа;
строки;
логические величины (аналоги 1 и О, "да" и
"нет", "истина" и "ложь"). Эти типы данных называют базовыми.
Каждая единица информации хранится в ячейках памяти компьютера, имеющих свои адреса.
В языках программирования введено понятие переменной, позволяющее отвлечься от конкретных адресов и обращаться к содержимому памяти с помощью идентификатора или имени - последовательности, содержащей английские буквы, цифры, символы подчеркивания и начинающейся не с цифры.
Слайд 336. Уровень языка программирования
Классификация языков программирования по критерию детализации предписаний:
машинные (самого низкого уровня);
машинно-ориентированные (ассемблеры);
машинно-независимые (высокого уровня).
Слайд 34В зависимости от детализации предписаний определяют уровень языка программирования (чем
меньше детализация, тем выше уровень). По данному критерию различают следующие
языки программирования:машинные (самого низкого уровня);
машинно-ориентированные (ассемблеры);
машинно-независимые (высокого уровня).
Машинные и машинно-ориентированные языки требуют подробного описания самых мелких деталей процесса обработки данных.
Язык ассемблера — это машинно-зависимый язык низкого уровня, в котором отдельным машинным командам соответствуют мнемонические (легко запоминаемые) имена, записываемые в текстовом виде.
Языки высокого уровня более разнообразны и интуитивно понятны для человека.
Преимущества:
универсальность - программа, написанная на таком языке, может выполняться на разных машинах;
независимость от аппаратуры, т.к. языки высокого уровня в значительной мере являются машинно-независимыми.