Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
8 класс Л.С. Атанасян Геометрия 7-9 Савченко Е.М., учитель математики, МОУ
Содержание
- 1. 8 класс Л.С. Атанасян Геометрия 7-9 Савченко Е.М., учитель математики, МОУ
- 2. №664. Прямая АМ – касательная
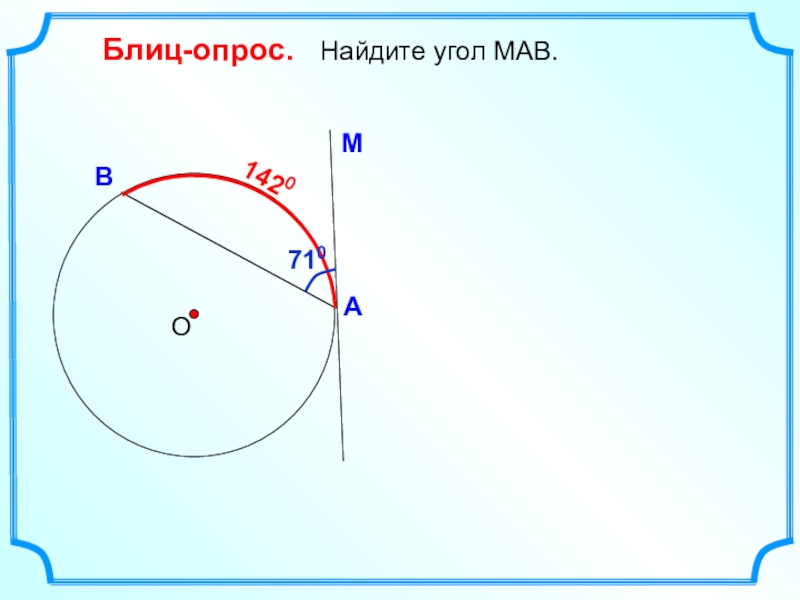
- 3. Блиц-опрос. Найдите угол МАВ. О1420710
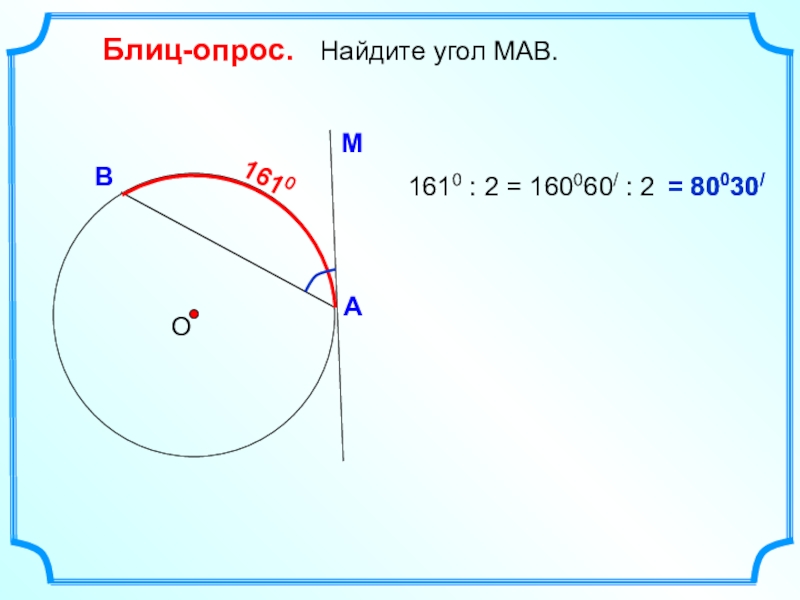
- 4. Блиц-опрос. Найдите угол МАВ.
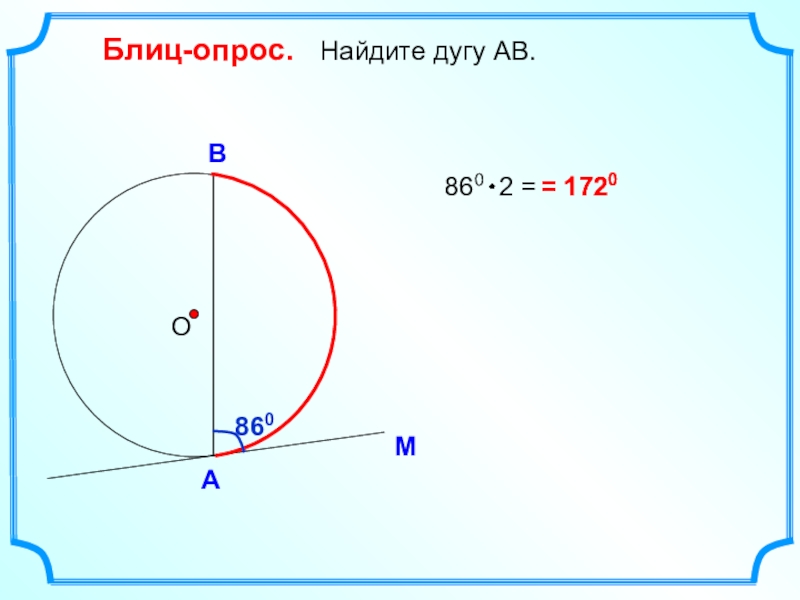
- 5. Блиц-опрос. Найдите дугу АВ. МАВО= 1720 8601720
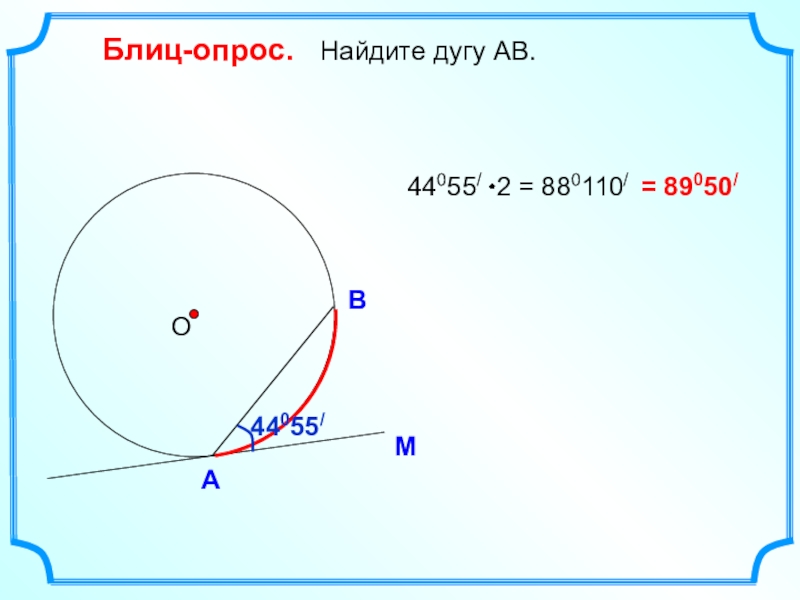
- 6. Блиц-опрос. Найдите дугу АВ. МАВО= 89050/ 44055/
- 7. №670. Через точку А
- 8. ?6 №671. Через точку А
- 9. №672. Через точку А,
- 10. АСВ Свойство медиан треугольника. Медианы
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
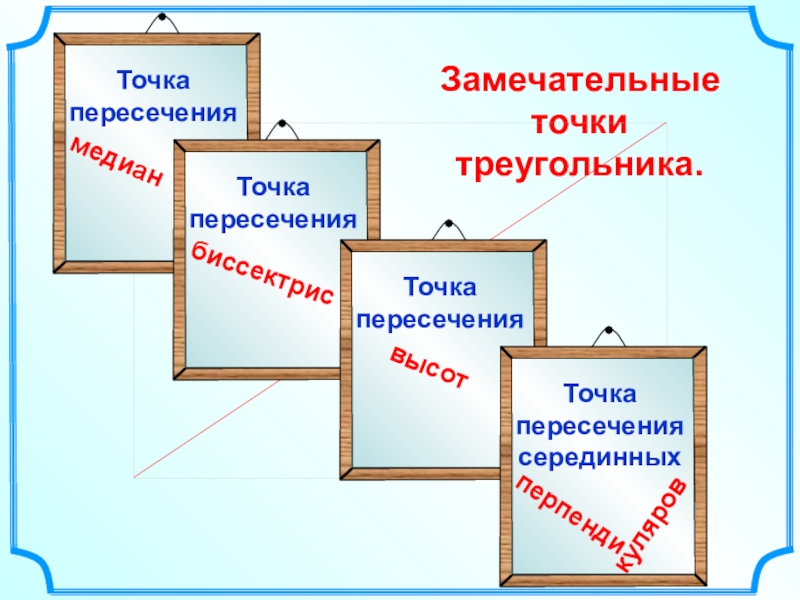
- 19. Замечательные точки треугольника.
- 20. Треугольник, который опирается на острие иглы
- 21. АВСКМТВысоты тупоугольного треугольника пересекаются в точке О,
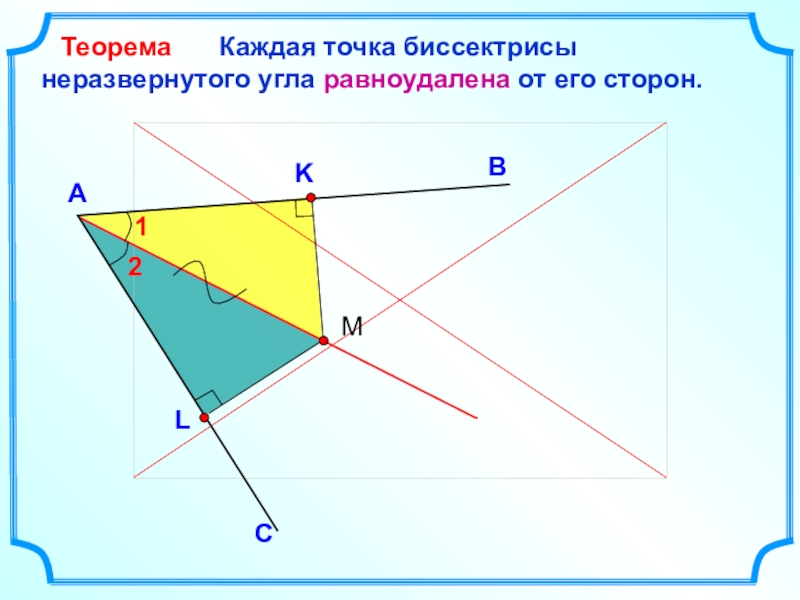
- 22. Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника
- 23. Эта точка замечательная – точка пересечения серединных
- 24. Скачать презентанцию
№664. Прямая АМ – касательная к окружности, АВ – хорда этой окружности. Докажите, что угол МАВ измеряется половиной дуги АВ, расположенной внутри угла МАВ.О
Слайды и текст этой презентации
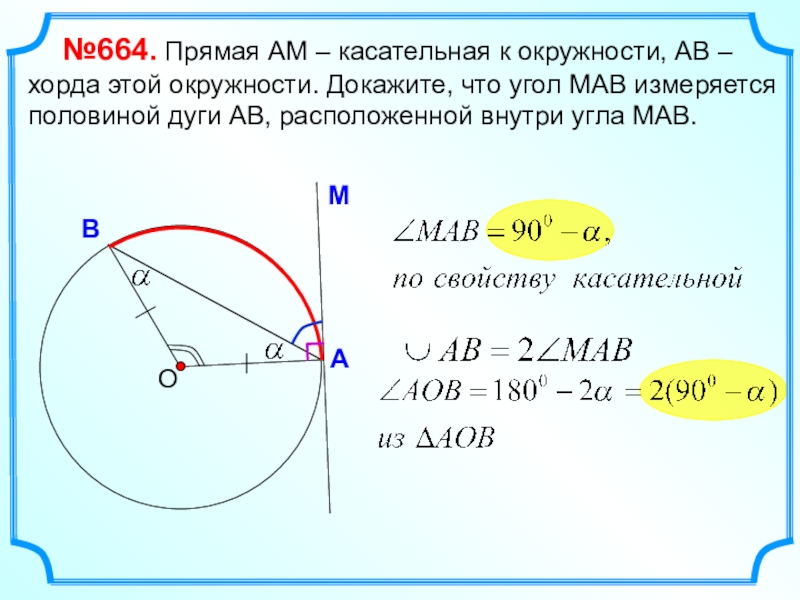
Слайд 2 №664. Прямая АМ – касательная к окружности, АВ
– хорда этой окружности. Докажите, что угол МАВ измеряется половиной
дуги АВ, расположенной внутри угла МАВ.О
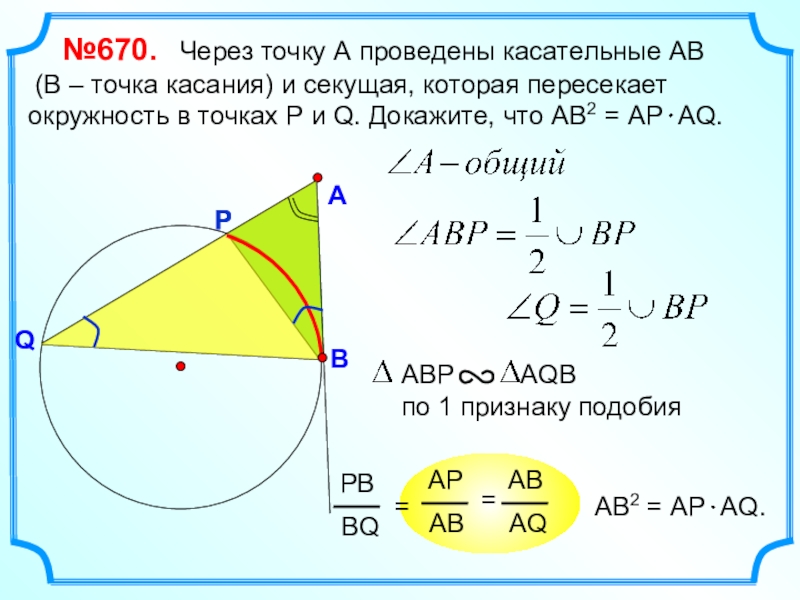
Слайд 7 №670. Через точку А проведены касательные АВ
(В – точка касания) и секущая, которая пересекает окружность в
точках Р и Q. Докажите, что АВ2 = АР АQ.АВ
АQ
Р
Слайд 8?
6
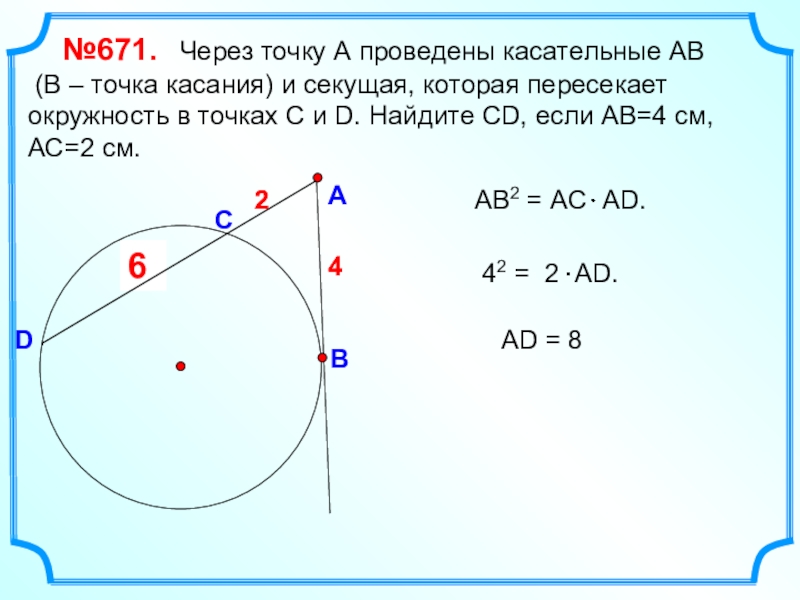
№671. Через точку А проведены касательные АВ
(В – точка касания) и секущая, которая пересекает окружность в
точках С и D. Найдите СD, если АВ=4 см,АС=2 см.
4
2
4
2
АD = 8
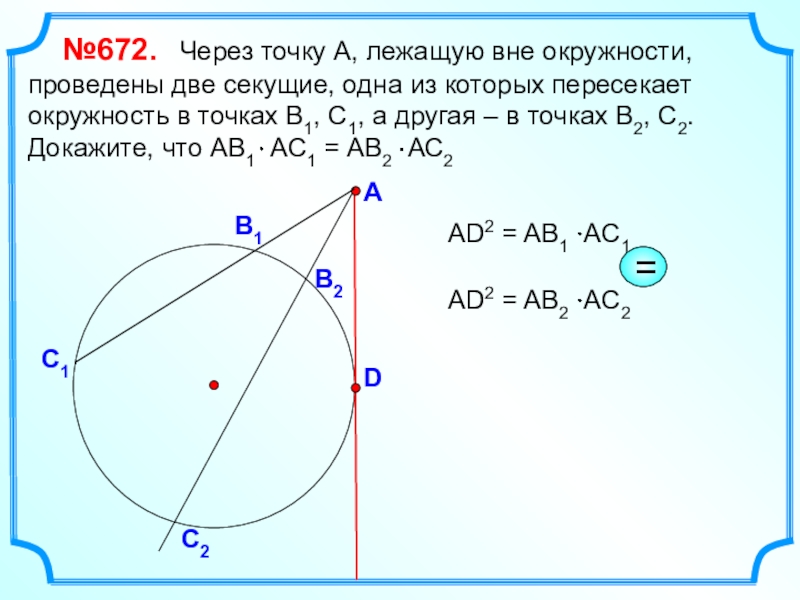
Слайд 9 №672. Через точку А, лежащую вне окружности,
проведены две секущие, одна из которых пересекает окружность в точках
В1, С1, а другая – в точках В2, С2. Докажите, что АВ1 АС1 = АВ2 АС2А
=
Слайд 10А
С
В
Свойство медиан треугольника.
Медианы треугольника пересекаются в
одной точке, которая делит каждую медиану в отношении 2:1, считая
от вершины.В1
А1
О
СО
С1О
=
С1
1
Слайд 12
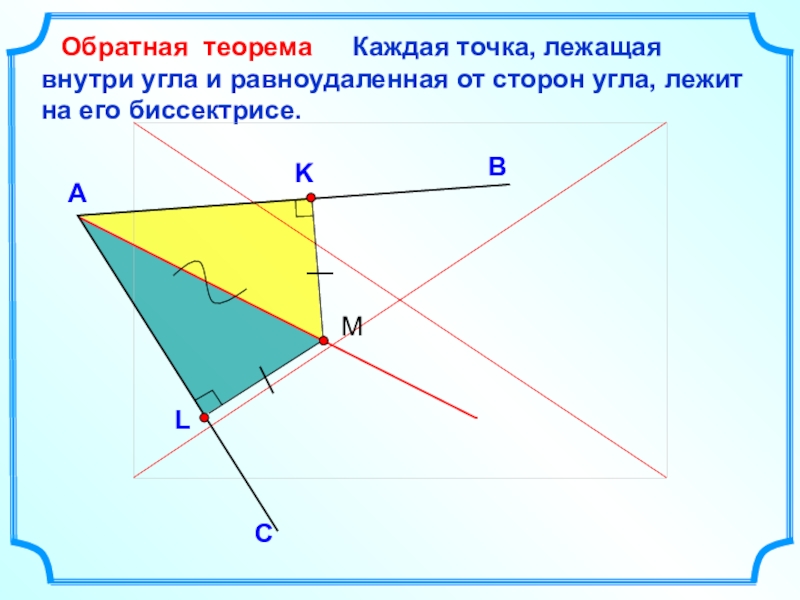
Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
В
А
Обратная теорема
С
Слайд 13
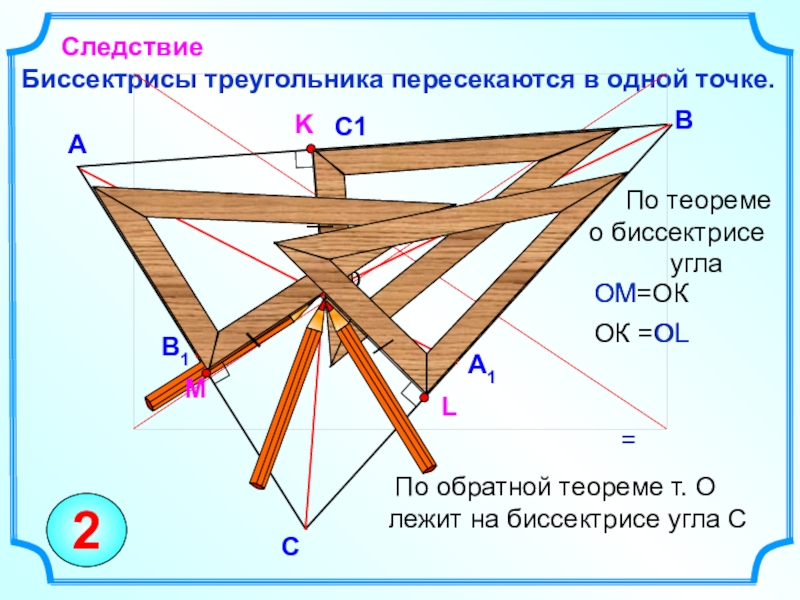
Биссектрисы треугольника пересекаются в одной точке.
В
А
Следствие
С
ОМ=ОК
По теореме о биссектрисе
угла
=
По обратной теореме т. О лежит на биссектрисе угла С
ОМ
ОL
2
Слайд 14
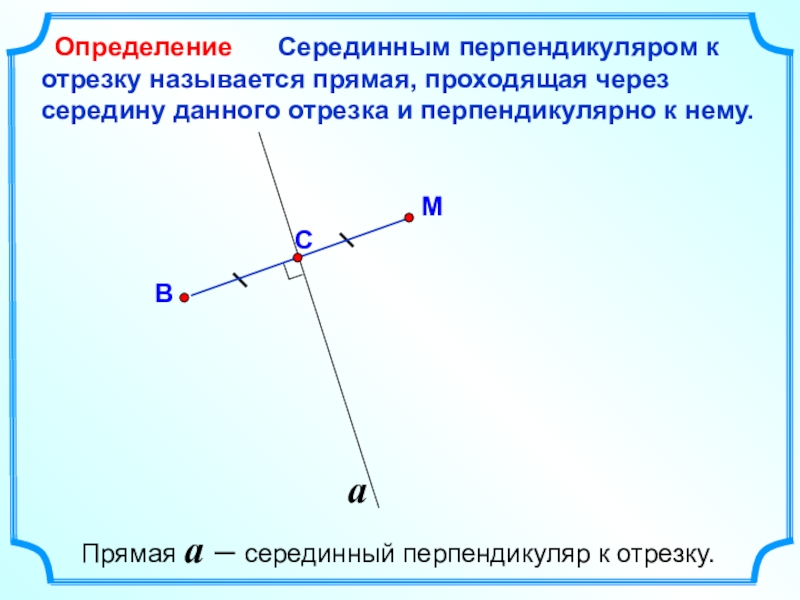
Серединным перпендикуляром к отрезку
называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему.М
В
Определение
Прямая a – серединный перпендикуляр к отрезку.
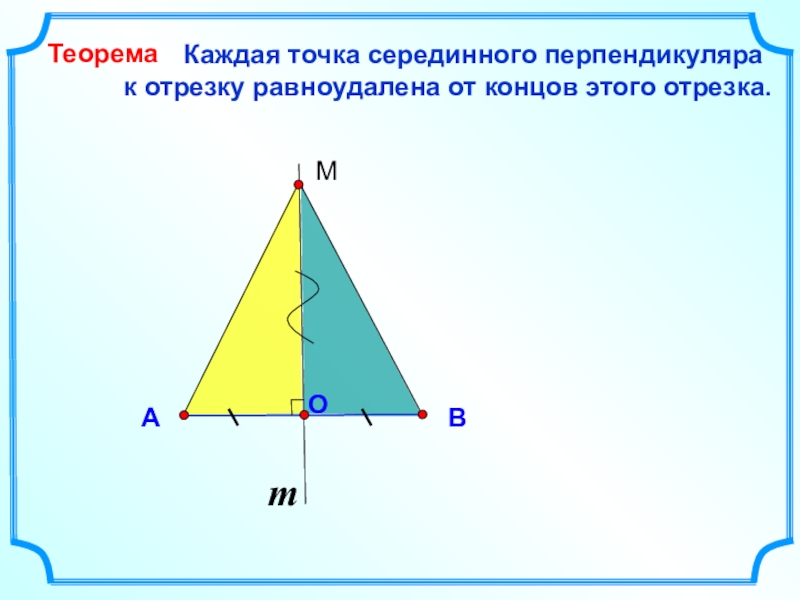
Слайд 15
Каждая точка серединного перпендикуляра
к отрезку равноудалена от концов этого отрезка. B
A
Теорема
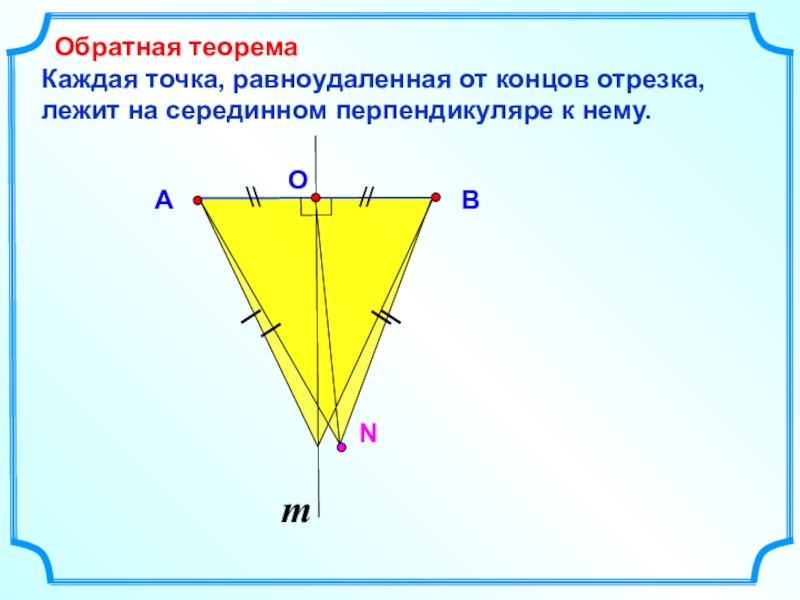
Слайд 16
Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Обратная теорема
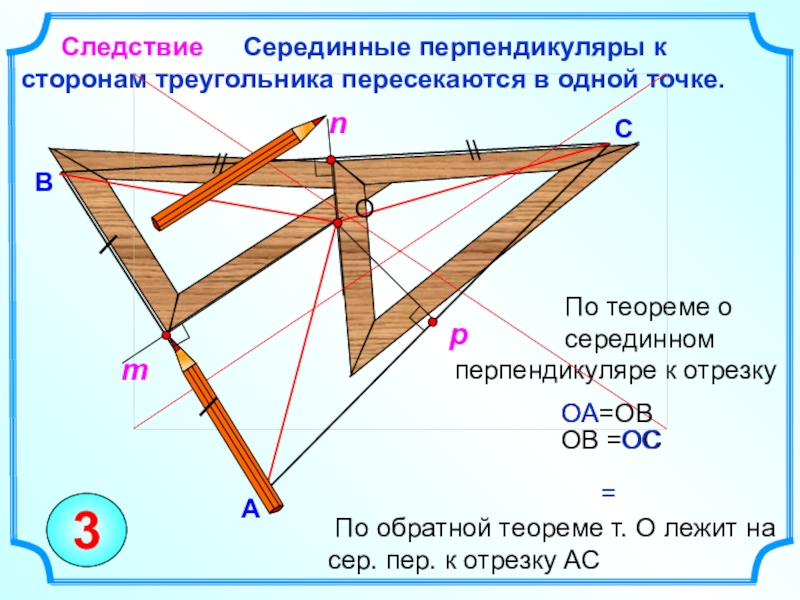
Слайд 17 По теореме
о
серединном
перпендикуляре к отрезку Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
C
B
Следствие
A
ОA=ОB
ОB =ОC
=
По обратной теореме т. О лежит на сер. пер. к отрезку АС
ОA
ОC
3
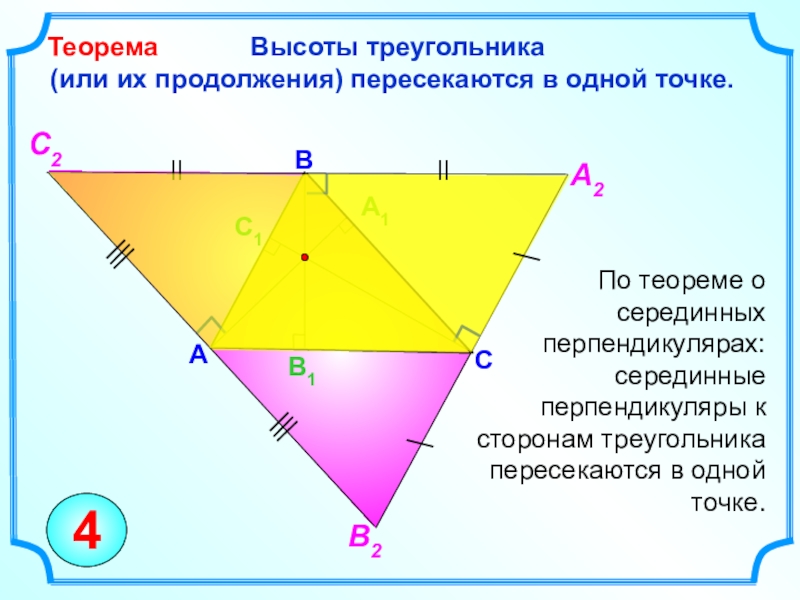
Слайд 18
Высоты треугольника
(или их продолжения) пересекаются в одной точке. Теорема
C
B
A
По теореме о серединных перпендикулярах: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
4
Слайд 20
Треугольник, который опирается на острие иглы в точке пересечения
медиан, находится в равновесии!
Точка, обладающая таким свойством, называется
центром тяжести треугольника.
Слайд 21А
В
С
К
М
Т
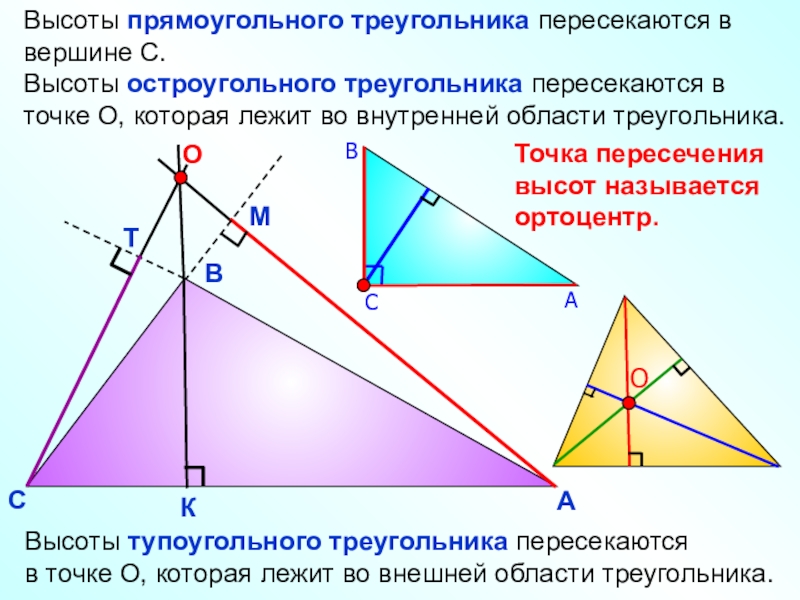
Высоты тупоугольного треугольника пересекаются
в точке О, которая лежит во
внешней области треугольника.
Высоты прямоугольного треугольника пересекаются в вершине С.
Высоты остроугольного
треугольника пересекаются в точке О, которая лежит во внутренней области треугольника. А
В
С
Точка пересечения
высот называется
ортоцентр.
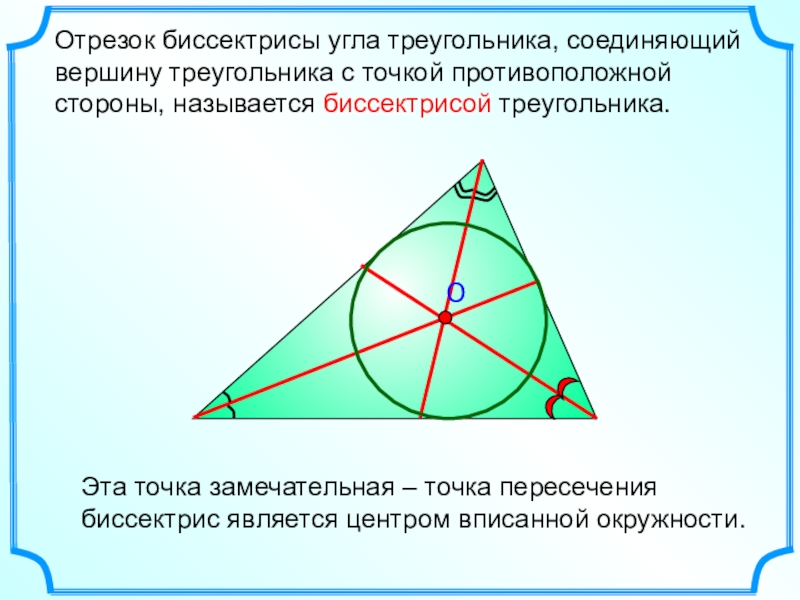
Слайд 22Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной
стороны, называется биссектрисой треугольника.
Эта точка замечательная – точка пересечения биссектрис
является центром вписанной окружности.
Слайд 23Эта точка замечательная –
точка пересечения
серединных перпендикуляров
к сторонам
треугольника
является центром описанной окружности.
Серединным перпендикуляром к отрезку
называется прямая, проходящая через
середину данного отрезка и
перпендикулярно к нему.
