Слайд 1Quick Quiz 4.1 Suppose you are standing directly behind someone
who steps back and accidentally stomps on your foot with
the heel of one shoe. Would you be better off if that person were (a) a large professional basketball player wearing sneakers (b) a petite woman wearing spike-heeled shoes?
Quick Quiz 4.2 A grandfather clock depends on the period of a pendulum to keep correct time. Suppose a grandfather clock is calibrated correctly and then a mischievous child slides the bob of the pendulum downward on the oscillating rod. Does the grandfather clock run (a) slow (b) fast (c) correctly?
Слайд 2Course of lectures «Contemporary Physics: Part1»
Lecture №7
Temperature.
Heat and the First
Law of Thermodynamics.
Слайд 3We now direct our attention to the study of thermodynamics,
which involves situations in which the temperature or state (solid,
liquid, gas) of a system changes due to energy transfers. As we shall see, thermodynamics is very successful in explaining the bulk properties of matter and the correlation between these properties and the mechanics of atoms and molecules.
Слайд 4Temperature and the Zeroth
Law of Thermodynamics
For purposes of the current
discussion, we assume that two objects are in thermal contact
with each other if energy can be exchanged between them by these processes due to a temperature difference.
Thermal equilibrium is a situation in which two objects would not exchange energy by heat or electromagnetic radiation if they were placed in thermal contact.
Слайд 5Temperature and the Zeroth
Law of Thermodynamics
Figure 19.1 The zeroth law
of thermodynamics. (a) and (b) If the temperatures of A
and B are measured to be the same by placing them in thermal contact with a thermometer (object C), no energy will be exchanged between them when they are placed in thermal contact with each other (c).
Слайд 6We can summarize these results in a statement known as
the zeroth law of thermodynamics (the law of equilibrium):
Temperature and
the Zeroth
Law of Thermodynamics
If objects A and B are separately in thermal equilibrium with a third object C, then A and B are in thermal equilibrium with each other.
Слайд 7Thermometers and the Celsius
Temperature Scale
As a result of thermal expansion,
the level of the mercury in the thermometer rises as
the mercury is heated by water in the test tube.
Слайд 8The Constant-Volume Gas Thermometer
and the Absolute Temperature Scale
A constant-volume gas
thermometer measures the pressure of the gas contained in the
flask immersed in the bath. The volume of gas in the flask is kept constant by raising or lowering reservoir B to keep the mercury level in column A constant.
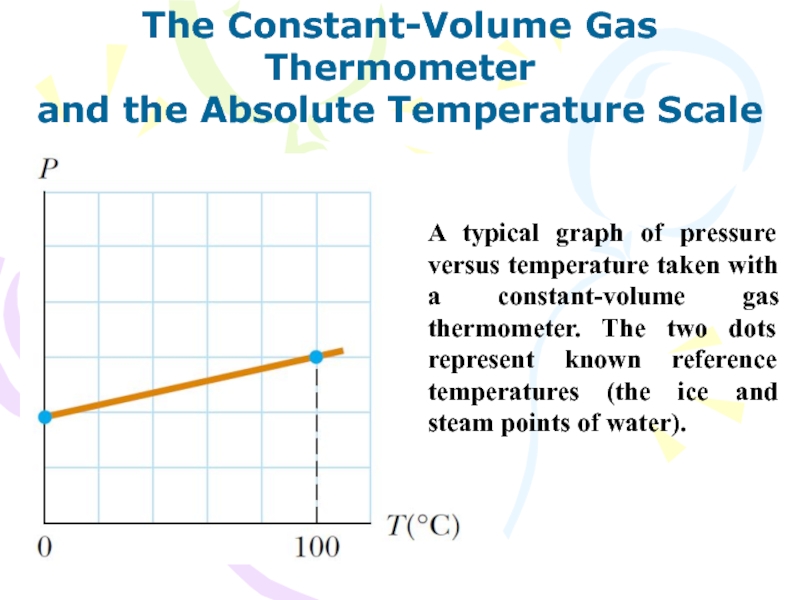
Слайд 9The Constant-Volume Gas Thermometer
and the Absolute Temperature Scale
A typical graph
of pressure versus temperature taken with a constant-volume gas thermometer.
The two dots represent known reference temperatures (the ice and steam points of water).
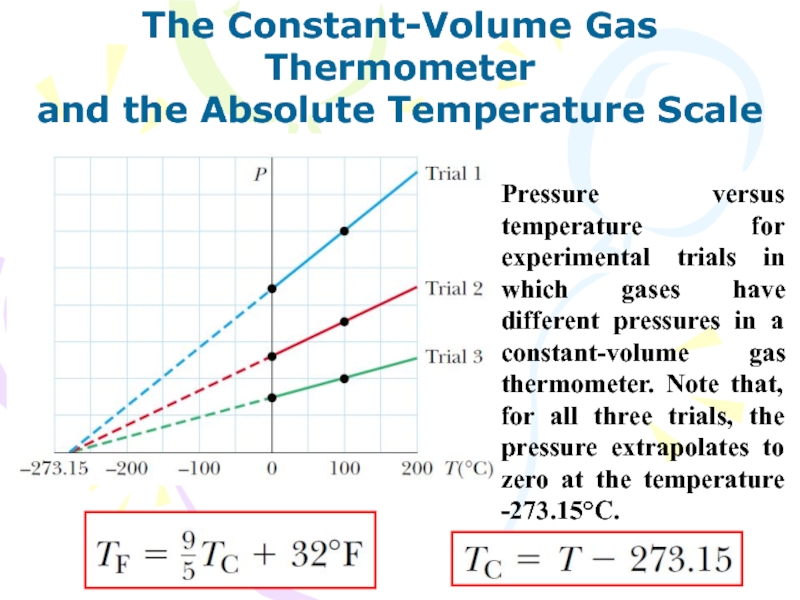
Слайд 10The Constant-Volume Gas Thermometer
and the Absolute Temperature Scale
Pressure versus temperature
for experimental trials in which gases have different pressures in
a constant-volume gas thermometer. Note that, for all three trials, the pressure extrapolates to zero at the temperature -273.15°C.
Слайд 11Thermal Expansion of Solids
and Liquids
Thermal expansion is a consequence
of the change in the average separation between the atoms
in an object.
Слайд 12Thermal Expansion of Solids
and Liquids
average coefficient of linear expansion
(9.1)
(9.2)
A
cavity in a piece of material expands in the same
way as if the cavity were filled with the material.
Слайд 13Thermal Expansion of Solids
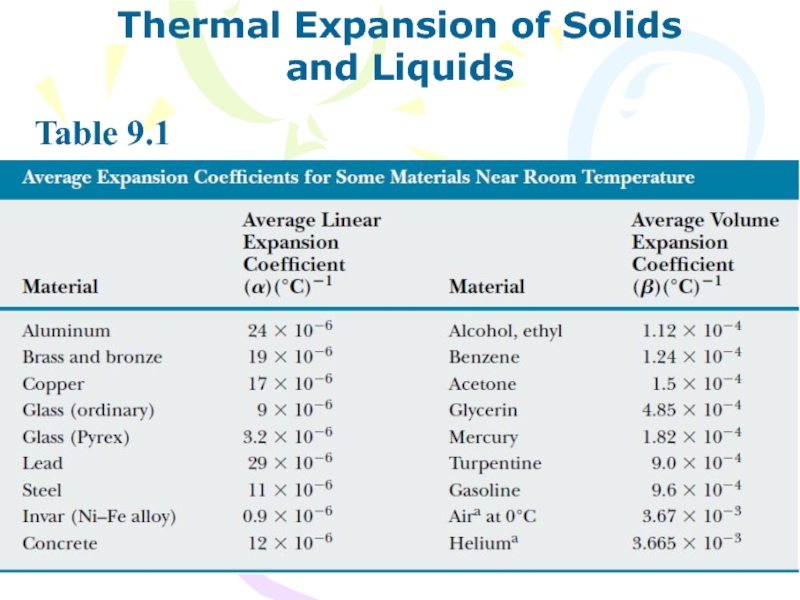
and Liquids
Table 9.1
Слайд 14Thermal Expansion of Solids
and Liquids
β is the average coefficient
of volume expansion.
(9.3)
Слайд 15Thermal Expansion of Solids
and Liquids
Слайд 16Thermal Expansion of Solids
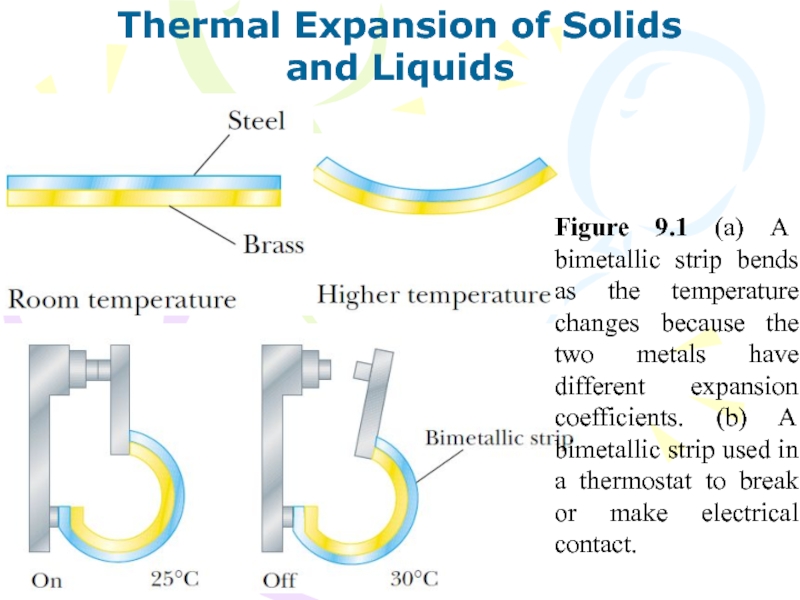
and Liquids
Figure 9.1 (a) A bimetallic
strip bends as the temperature changes because the two metals
have different expansion coefficients. (b) A bimetallic strip used in a thermostat to break or make electrical contact.
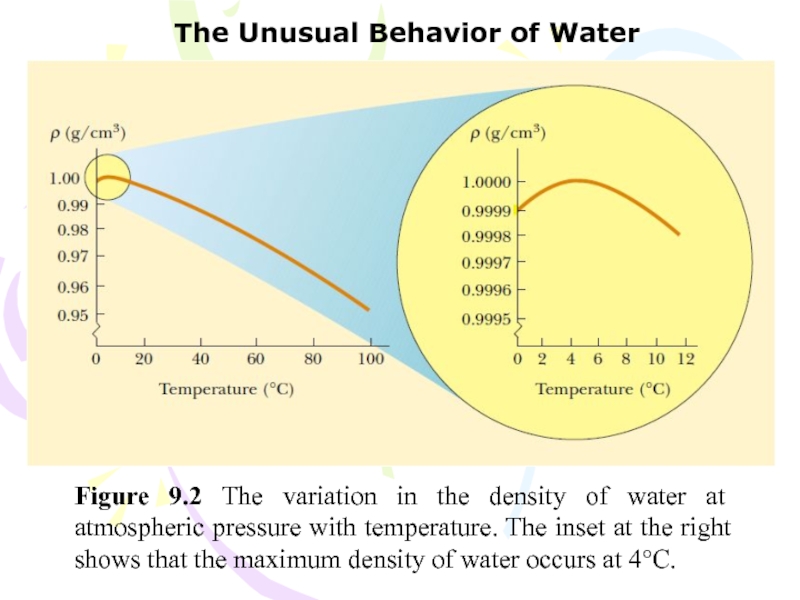
Слайд 17The Unusual Behavior of Water
Figure 9.2 The variation in the
density of water at atmospheric pressure with temperature. The inset
at the right shows that the maximum density of water occurs at 4°C.
Слайд 18Macroscopic Description of an Ideal Gas
It is convenient to express
the amount of gas in a given volume in terms
of the number of moles n. One mole of any substance is that amount of the substance that contains Avogadro’s number NA = 6.022 ) 1023 of constituent particles (atoms or molecules).
(9.4)
Слайд 19Macroscopic Description of an Ideal Gas
(9.5)
Equation of state for an
ideal gas
Слайд 20Macroscopic Description of an Ideal Gas
Figure 9.4 A bottle of
champagne is shaken and opened. Liquid spews out of the
opening. A common misconception is that the pressure inside the bottle is increased due to the shaking.
Слайд 21Macroscopic Description of an Ideal Gas
(9.6)
Слайд 22Heat and Internal Energy
Internal energy is all the energy of
a system that is associated with its microscopic components—atoms and
molecules—when viewed from a reference frame at rest with respect to the center of mass of the system.
Heat is defined as the transfer of energy across the boundary of a system due to a temperature difference between the system and its surroundings.
Слайд 23Units of Heat
An energy unit related to thermal processes, the
calorie (cal), which is defined as the amount of energy
transfer necessary to raise the temperature of 1 g of water from 14.5°C to 15.5°C. (Note that the “Calorie,” written with a capital “C” and used in describing the energy content of foods, is actually a kilocalorie.) The unit of energy in the U.S. customary system is the British thermal unit (Btu), which is defined as the amount of energy transfer required to raise the temperature of 1 lb of water from 63°F to 64°F.
Scientists are increasingly using the SI unit of energy, the joule, when describing thermal processes.
Слайд 24The Mechanical Equivalent of Heat
(9.7)
Figure 9.5 Joule’s experiment for determining
the mechanical equivalent of heat. The falling blocks rotate the
paddles, causing the temperature of the water to increase.
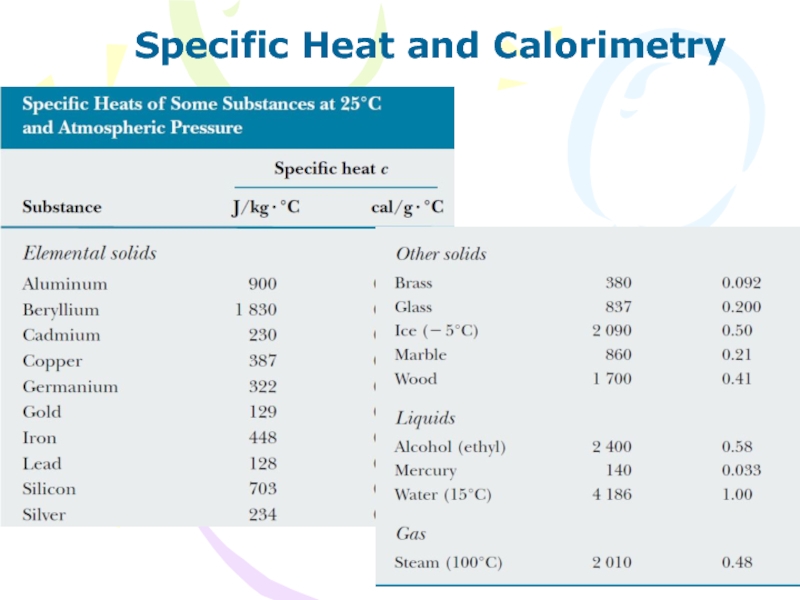
Слайд 25Specific Heat and Calorimetry
The heat capacity C of a particular
sample of a substance is defined as the amount of
energy needed to raise the temperature of that sample by 1°C.
The specific heat c of a substance is the heat capacity per unit mass.
(9.8)
(9.9)
Слайд 26Specific Heat and Calorimetry
From this definition, we can relate the
energy Q transferred between a sample of mass m of
a material and its surroundings to a temperature change ∆T as
(9.10)
Слайд 28Conservation of Energy: Calorimetry
(9.11)
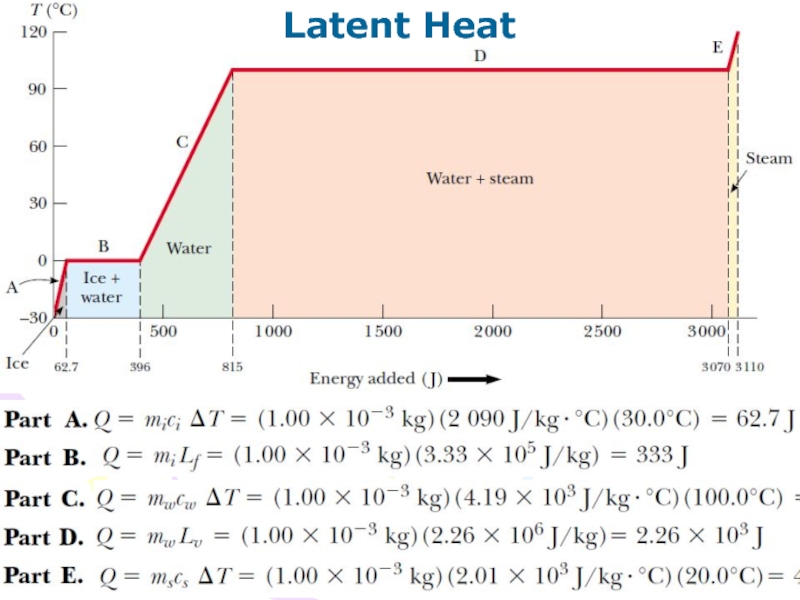
Слайд 29Latent Heat
From the definition of latent heat, and again choosing
heat as our energy transfer mechanism, we find that the
energy required to change the phase of a given mass m of a pure substance is
(9.12)
Latent heat of fusion Lf is the term used when the phase change is from solid to liquid (to fuse means “to combine by melting”), and latent heat of vaporization Lv is the term used when the phase change is from liquid to gas (the liquid “vaporizes”).
Слайд 31Work and Heat in Thermodynamic Processes
Figure 9.6 Work is done
on a gas contained in a cylinder at a pressure
P as the piston is pushed downward so that the gas is compressed.
(9.13)
(9.14)
Слайд 32Work and Heat in Thermodynamic Processes
Figure 9.7 A gas is
compressed quasi-statically (slowly) from state i to state f. The
work done on the gas equals the negative of the area under the PV curve.
The work done on a gas in a quasi-static process that takes the gas from an initial state to a final state is the negative of the area under the curve on a PV diagram, evaluated between the initial and final states.
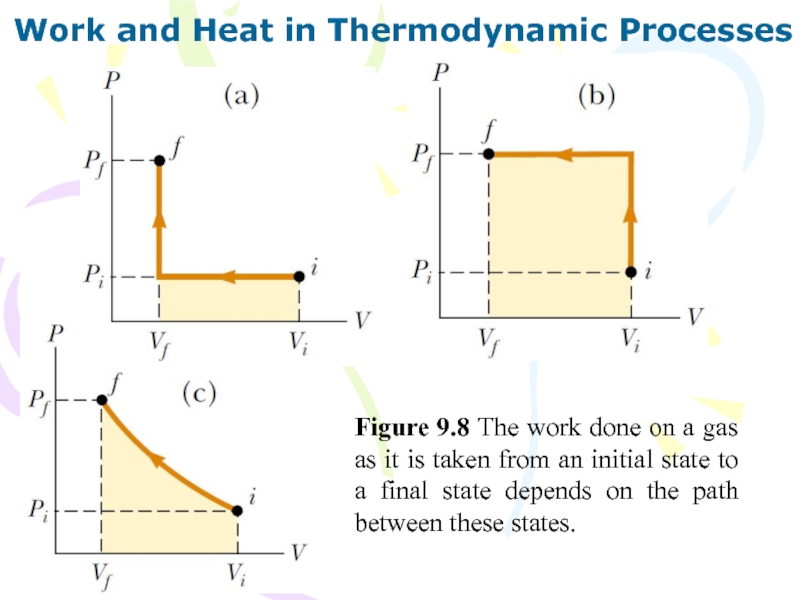
Слайд 33Work and Heat in Thermodynamic Processes
Figure 9.8 The work done
on a gas as it is taken from an initial
state to a final state depends on the path between these states.
Слайд 34Work and Heat in Thermodynamic Processes
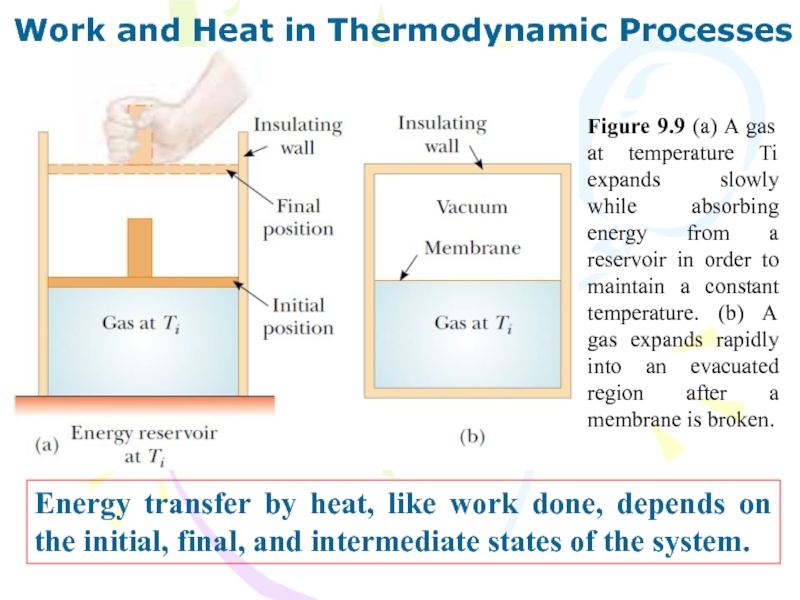
Energy transfer by heat, like
work done, depends on the initial, final, and intermediate states
of the system.
Figure 9.9 (a) A gas at temperature Ti expands slowly while absorbing energy from a reservoir in order to maintain a constant temperature. (b) A gas expands rapidly into an evacuated region after a membrane is broken.
Слайд 35The First Law of Thermodynamics
the change in the internal energy
of the system,
independent of the path.
the internal energy
the change
in internal energy
The first law of thermodynamics
(9.15)
Слайд 36The First Law of Thermodynamics
First, consider an isolated system—that is,
one that does not interact with its surroundings.
The internal energy
Eint of an isolated system remains constant.
Слайд 37The First Law of Thermodynamics
Next, consider the case of a
system (one not isolated from its surroundings) that is taken
through a cyclic process—that is, a process that starts and ends at the same state.
In a cyclic process, the net work done on the system per cycle equals the area enclosed by the path representing the process on a PV diagram.
Слайд 38Quick Quiz 5.1
Two objects, with different sizes, masses, and
temperatures, are placed in thermal contact. Energy travels (a) from
the larger object to the smaller object (b) from the object with more mass to the one with less (c) from the object at higher temperature to the object at lower temperature.
Слайд 39Quick Quiz 5.2
Consider the following pairs of materials. Which
pair represents two materials, one of which is twice as
hot as the other? (a) boiling water at 100°C, a glass of water at 50°C (b) boiling water at 100°C, frozen methane at -50°C (c) an ice cube at -20°C, flames from a circus fire-eater at 233°C (d) No pair represents materials one of which is twice as hot as the other