TA1

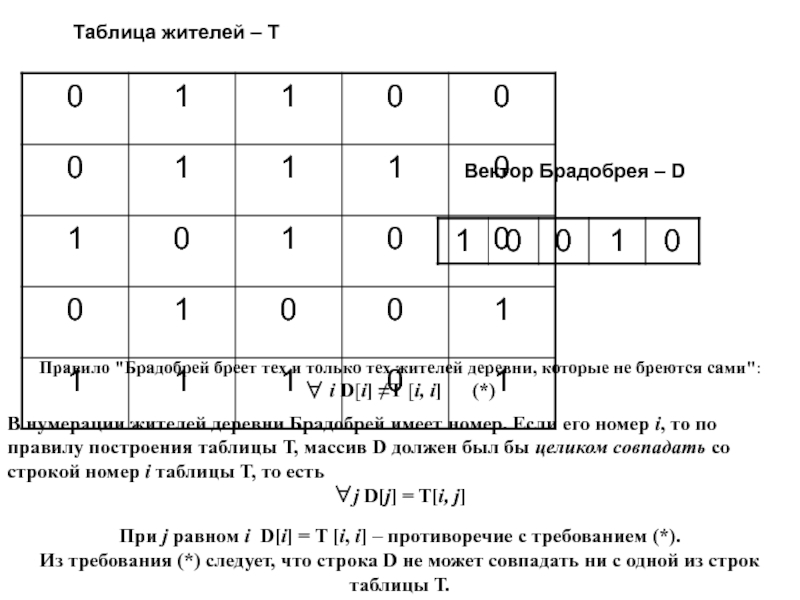
не бреются сами":

∀ i D[i] ≠Т [i, i] (*)

В нумерации жителей деревни Брадобрей имеет номер. Если его номер i, то по правилу построения таблицы Т, массив D должен был бы целиком совпадать со строкой номер i таблицы Т, то есть
∀j D[j] = T[i, j]

При j равном i D[i] = Т [i, i] – противоречие с требованием (*).
Из требования (*) следует, что строка D не может совпадать ни с одной из строк таблицы Т.

Таблица жителей – T

Вектор Брадобрея – D

цикла" в программе на Паскале:
х:= 1; repeat { какие-то действия, которые не

изменяют значение переменной x. }; until x>10;

if z=0 then
writeln("He зациклится") (A)
else
writein("зациклится");

if z=0 then
repeat until false (B)
else writein("зациклится");

однозначное отображение f : Z0 → X между множеством

неотрицательных целых чисел Z0 и множеством X.
Определение 2. Множество называют не более чем счетным, если оно счетно или конечно.
Определение 3. Перечислением или нумерацией множества X называется отображение
f : Z0 → X множества Z0 на множество X.
Перечисление f определяет на множестве X некоторую бесконечную последовательность
x0, x1, x2 … (xi = f ( i ).
Если отображение f - взаимно однозначно, то f называют перечислением или нумерацией без повторений.
Определение 4. Множество X называется эффективно счетным, если существует функция f : Z0 → X , устанавливающая взаимно однозначное соответствие между множествами Z0 и X такая, что f и f -1 - вычислимые функции.
Теорема 1. Следующие множества являются эффективно счетными:

МНР включает четыре типа команд Z(n), S(n), T(m, n),
J(m,

n, q), где

Определим взаимно однозначное отображение

β (Z (n) ) = 4 × (n - 1);
β (S (n) ) = 4 × (n - 1) + 1;

произвольная программа для МНР.
Определим взаимно однозначное отображение


Определение 5.

Пусть f – n-местная функция, вычислимая по программе P с геделевым номером m = γ (P). Число m будем называть индексом функции f. Вычислимую функцию от n переменных с индексом m будем обозначать символом

Каждая n-местная вычислимая функция f представлена в перечислении

проблемы Pr1 приводит к решению другой проблемы Pr2. В этом

случае говорят, что проблема Pr2 сводится к проблеме Pr1. Таким образом, если проблема Pr2 сводится к проблеме Pr1, то из разрешимости Pr1 следует разрешимость Pr2 и, наоборот, из неразрешимости Pr2 следует неразрешимость Pr1.

формулировкой проблемы в форме: «Остановится ли МНР, работая по программе

с начальной конфигурацией (x)?». Другими словами: «Применима ли программа к своему кодовому номеру?».
Теорему 9 часто интерпретируют как утверждение о неразрешимости проблемы остановки, в которой говорится, что не существует общего метода, устанавливающего, остановится ли некоторая конкретная программа, запущенная с некоторым конкретным набором начальных данных.
Смысл этого утверждения для теоретического программирования очевиден: не существует общего метода проверки программ на наличие в них бесконечных циклов.