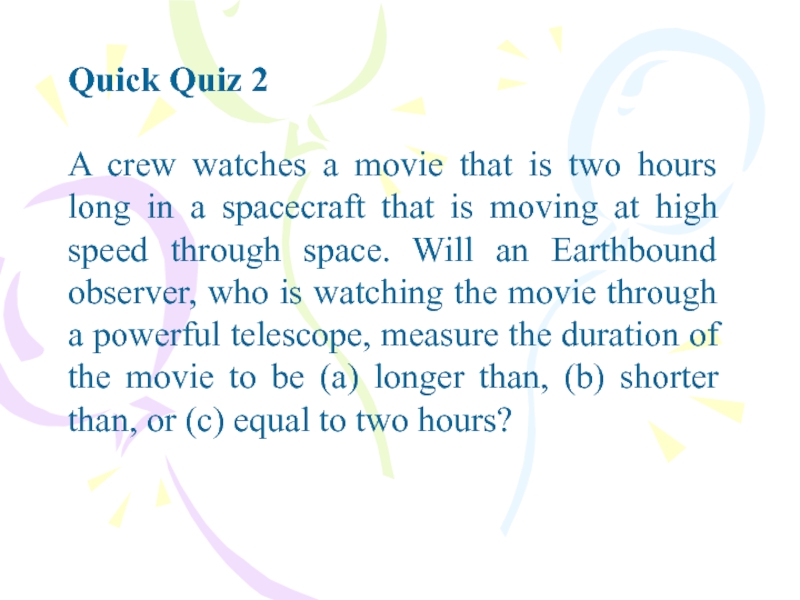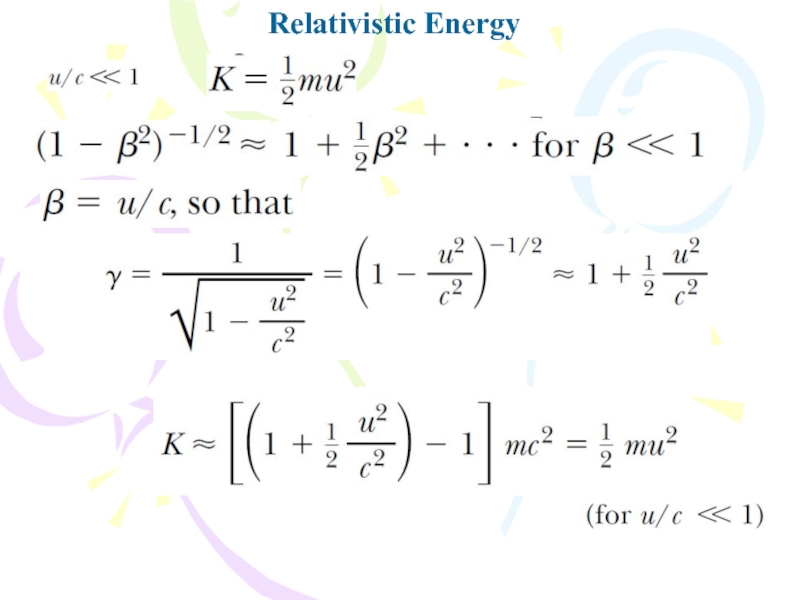Слайд 1Quick Quiz 1
A baseball pitcher with a 90-mi/h fastball throws
a ball while standing on a railroad flatcar moving at
110 mi/h. The ball is thrown in the same direction as that of the velocity of the train. Applying the Galilean velocity transformation equation, the speed of the ball relative to the Earth is (a) 90 mi/h
(b) 110 mi/h (c) 20 mi/h (d) 200 mi/h (e) impossible to determine.
Слайд 2Quick Quiz 2
A crew watches a movie that is two
hours long in a spacecraft that is moving at high
speed through space. Will an Earthbound observer, who is watching the movie through a powerful telescope, measure the duration of the movie to be (a) longer than, (b) shorter than, or (c) equal to two hours?
Слайд 3Quick Quiz 3
Suppose astronauts are paid according to the amount
of time they spend traveling in space. After a long
voyage traveling at a speed approaching c, would a crew rather be paid according to (a) an Earth-based clock, (b) their spacecraft’s clock, or (c) either clock?
Слайд 4Quick Quiz 4
You are packing for a trip to another
star. During the journey, you will be traveling at 0.99c.
You are trying to decide whether you should buy smaller sizes of your clothing, because you will be thinner on your trip, due to length contraction. Also, you are considering saving money by reserving a smaller cabin to sleep in, because you will be shorter when you lie down. Should you (a) buy smaller sizes of clothing, (b) reserve a smaller cabin, (c) do neither of these, or (d) do both of these?
Слайд 5Course of lectures «Contemporary Physics: Part2»
Lecture №7
The Lorentz Transformation Equations.
The Lorentz Velocity Transformation
Equations. Relativistic Linear Momentum and
the Relativistic Form
of Newton’s Laws. Relativistic Energy. Mass and Energy. The General Theory of Relativity.
Слайд 6The Lorentz Transformation Equations
The equations that are valid for all
speeds and enable us to transform coordinates from S to
S’ are the Lorentz transformation equations:
Слайд 7The Lorentz Transformation Equations
If we wish to transform coordinates in
the S’ frame to coordinates in the S frame, we
simply replace v by -v and interchange the primed and unprimed coordinates:
the Lorentz transformation equations should reduce to the Galilean equations
as v approaches zero,
Слайд 8The Lorentz Transformation Equations
In many situations, we would like to
know the difference in coordinates between two events or the
time interval between two events as seen by observers O and O’. We can accomplish this by writing the Lorentz equations in a form suitable for describing pairs of events. We can express the differences between the four variables x, x’, t, and t’ in the form:
the differences measured by observer O’
the differences measured by observer O
Слайд 9The Lorentz Velocity Transformation Equations
Suppose two observers in relative motion
with respect to each other are both observing the motion
of an object. Previously, we defined an event as occurring at an instant of time. Now, we wish to interpret the “event” as the motion of the object. We know that the Galilean velocity transformation is valid for low speeds. How do the observers’ measurements of the velocity of the object relate to each other if the speed of the object is close to that of light? Once again S’ is our frame moving at a speed v relative to S. Suppose that an object has a velocity component u’x measured in the S frame, where
(1)
Слайд 10The Lorentz Velocity Transformation Equations
If the object has velocity components
along the y and z axes, the components as measured
by an observer in S’ are
When v is much smaller than c (the nonrelativistic case), the denominator of Equation 1 approaches unity, and so
which is the Galilean velocity transformation equation.
In another extreme, when Equation 1 becomes
Слайд 11Relativistic Linear Momentum and
the Relativistic Form of Newton’s Laws
We have
seen that in order to describe properly the motion of
particles within the framework of the special theory of relativity, we must replace the Galilean transformation equations by the Lorentz transformation equations. Because the laws of physics must remain unchanged under the Lorentz transformation, we must generalize Newton’s laws and the definitions of linear momentum and energy to
conform to the Lorentz transformation equations and the principle of relativity. These generalized definitions should reduce to the classical (nonrelativistic) definitions for
Слайд 12First, recall that the law of conservation of linear momentum
states that when two particles (or objects that can be
modeled as particles) collide, the total momentum of the isolated system of the two particles remains constant. Suppose that we observe this collision in a reference frame S and confirm that the momentum of the system is conserved. Now imagine that the momenta of the particles are measured by an observer in a second reference frame S" moving with velocity v relative to the first frame. Using the Lorentz velocity transformation equation and the classical definition of linear momentum, p = mu (where u is the velocity of a particle), we find that linear momentum is not measured to be conserved by the observer in S’. However, because the laws of physics are the same in all inertial frames, linear momentum of the system must be conserved in all frames. We have a contradiction.
Relativistic Linear Momentum and
the Relativistic Form of Newton’s Laws
Слайд 13Relativistic Linear Momentum and
the Relativistic Form of Newton’s Laws
In view
of this contradiction and assuming that the Lorentz velocity transformation
equation is correct, we must modify the definition of linear momentum to satisfy the following conditions:
• The linear momentum of an isolated system must be conserved in all collisions.
• The relativistic value calculated for the linear momentum p of a particle must approach the classical value mu as u approaches zero.
For any particle, the correct relativistic equation for linear momentum that satisfies these conditions is
where u is the velocity of the particle and m is the mass of the particle. When u is much less than c,
approaches unity and p approaches mu.
Слайд 14Relativistic Linear Momentum and
the Relativistic Form of Newton’s Laws
The relativistic
force F acting on a particle whose linear momentum is
p is defined as
This expression, which is the relativistic form of Newton’s second law, is reasonable because it preserves classical mechanics in the limit of low velocities and is consistent with conservation of linear momentum for an isolated system (F=0) both relativistically and classically.
Слайд 15Relativistic Energy
We have seen that the definition of linear momentum
requires generalization to make it compatible with Einstein’s postulates. This
implies that most likely the definition of kinetic energy must also be modified. To derive the relativistic form of the work–kinetic energy theorem, let us imagine a particle moving in one dimension along the x axis. The work done by the force F on the particle is
Слайд 16Relativistic Energy
Evaluating the integral, we find that
the work done by
a force acting on a system consisting of a single
particle equals the change in kinetic energy of the particle. Because we assumed that the initial speed of the particle is zero, we know that its initial kinetic energy is zero. We therefore conclude that the work W is equivalent to the relativistic kinetic energy K:
This equation is routinely confirmed by experiments using high-energy particle accelerators.
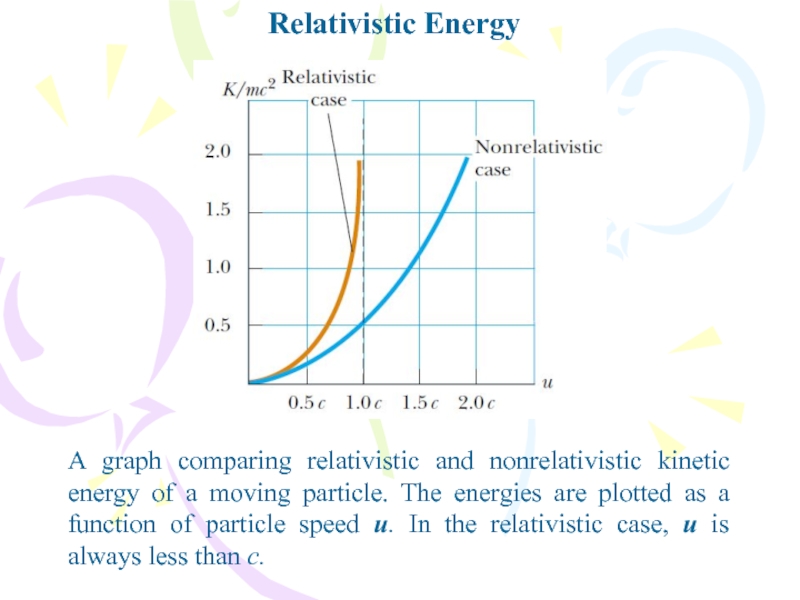
Слайд 18Relativistic Energy
A graph comparing relativistic and nonrelativistic kinetic energy of
a moving particle. The energies are plotted as a function
of particle speed u. In the relativistic case, u is always less than c.
Слайд 19Relativistic Energy
the rest energy ER of the particle
The term γmc2,
which does depend on the particle speed, is therefore the
sum of the kinetic and rest energies. We define γmc2 to be the total energy E:
This expression shows that a small mass corresponds to an enormous amount of energy, a concept fundamental to nuclear and elementary-particle physics.
Слайд 20Relativistic Energy
In many situations, the linear momentum or energy of
a particle is measured rather than its speed. It is
therefore useful to have an expression relating the total energy E to the relativistic linear momentum p.
Finally, note that because the mass m of a particle is independent of its motion, m must have the same value in all reference frames. For this reason, m is often called the invariant mass. On the other hand, because the total energy and linear momentum of a particle both depend on velocity, these quantities depend on the reference frame in which they are measured.
Слайд 21Relativistic Energy
When we are dealing with subatomic particles, it is
convenient to express their energy in electron volts because the
particles are usually given this energy by acceleration through a potential difference. The conversion factor is
For example, the mass of an electron is 9.11·10-31 kg. Hence, the rest energy of the electron is
Слайд 22Mass and Energy
Equation E=γmc2, which represents the total energy of
a particle, suggests that even when a particle is at
rest (γ=1) it still possesses enormous energy through its mass. The clearest experimental proof of the equivalence of mass and energy occurs in nuclear and elementary particle interactions in which the conversion of mass into kinetic energy takes place. Because of this, in relativistic situations, we cannot use the principle of conservation of energy. We must include rest energy as another form of energy storage.
This concept is important in atomic and nuclear processes, in which the change in mass is a relatively large fraction of the initial mass. For example, in a conventional nuclear reactor, the uranium nucleus undergoes fission, a reaction that results in several lighter fragments having considerable kinetic energy.
Слайд 23The General Theory of Relativity
Up to this point, we have
sidestepped a curious puzzle. Mass has two seemingly different properties:
a gravitational attraction for other masses and an inertial property that represents a resistance to acceleration. To designate these two attributes, we use the subscripts g and i and write
The value for the gravitational constant G was chosen to make the magnitudes of mg and mi numerically equal. Regardless of how G is chosen, however, the strict proportionality of mg and mi has been established experimentally to an extremely high degree: a few parts in 1012. Thus, it appears that gravitational mass and inertial mass may indeed be exactly proportional.
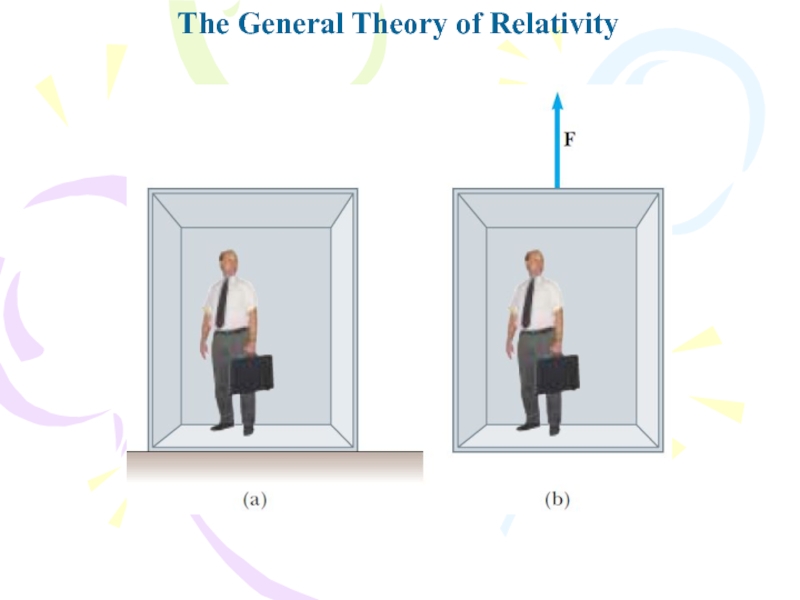
Слайд 24The General Theory of Relativity
Слайд 25The General Theory of Relativity
Слайд 26The General Theory of Relativity
The two postulates of Einstein’s general
theory of relativity are
• All the laws of nature have
the same form for observers in any frame of reference, whether accelerated or not.
• In the vicinity of any point, a gravitational field is equivalent to an accelerated frame of reference in the absence of gravitational effects. (This is the principle of equivalence.)
One interesting effect predicted by the general theory is that time is altered by gravity. A clock in the presence of gravity runs slower than one located where gravity is negligible. Consequently, the frequencies of radiation emitted by atoms in the presence of a strong gravitational field are red-shifted to lower frequencies when compared with the same emissions in the presence of a weak field. This gravitational red shift has been detected in spectral lines emitted by atoms in massive stars. It has also been verified on the Earth by comparing the frequencies of gamma rays emitted from nuclei separated vertically by about 20 m.
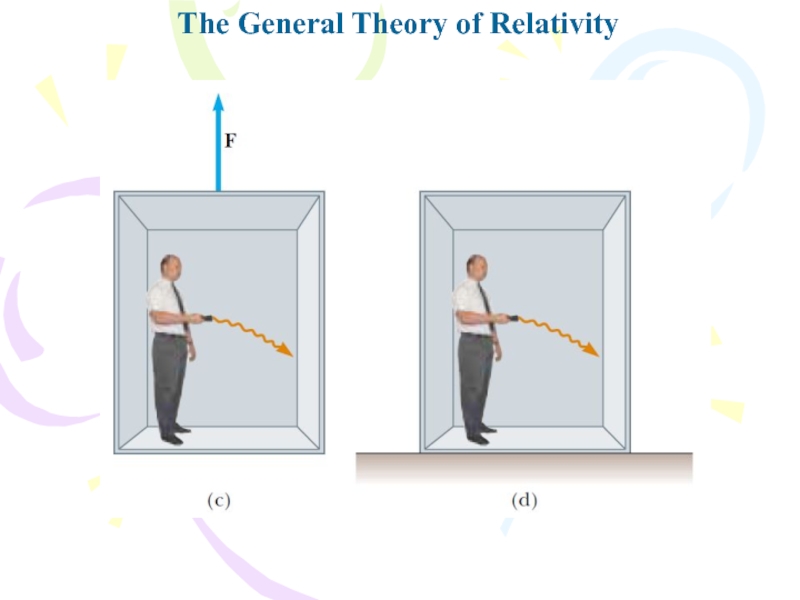
Слайд 27The General Theory of Relativity
The second postulate suggests that a
gravitational field may be “transformed away” at any point if
we choose an appropriate accelerated frame of reference—a freely falling one. Einstein developed an ingenious method of describing the acceleration necessary to make the gravitational field “disappear.” He specified a concept, the curvature of space–time, that describes the gravitational effect at every point. In fact, the curvature of space–time completely replaces Newton’s gravitational theory. According to Einstein, there is no such thing as a gravitational force. Rather, the presence of a mass causes a curvature of space–time in the vicinity of the mass, and this curvature dictates the space–time path that all freely moving objects must follow. In 1979, John Wheeler summarized Einstein’s general theory of relativity in a single sentence: “Space tells matter how to move and matter tells space how to curve.”
Слайд 28The General Theory of Relativity
As an example of the effects
of curved space–time, imagine two travelers moving on parallel paths
a few meters apart on the surface of the Earth and maintaining an exact northward heading along two longitude lines. As they observe each other near the equator, they will claim that their paths are exactly parallel. As they approach the North Pole, however, they notice that they are moving closer together, and they will actually meet at the North Pole. Thus, they will claim that they moved along parallel paths, but moved toward each other, as if there were an attractive force between them. They will make this conclusion based on their everyday experience of moving on flat surfaces. From our mental representation, however, we realize that they are walking on a curved surface, and it is the geometry of the curved surface that causes them to converge, rather than an attractive force. In a similar way, general relativity replaces the notion of forces with the movement of objects through curved space–time.
Слайд 29The General Theory of Relativity
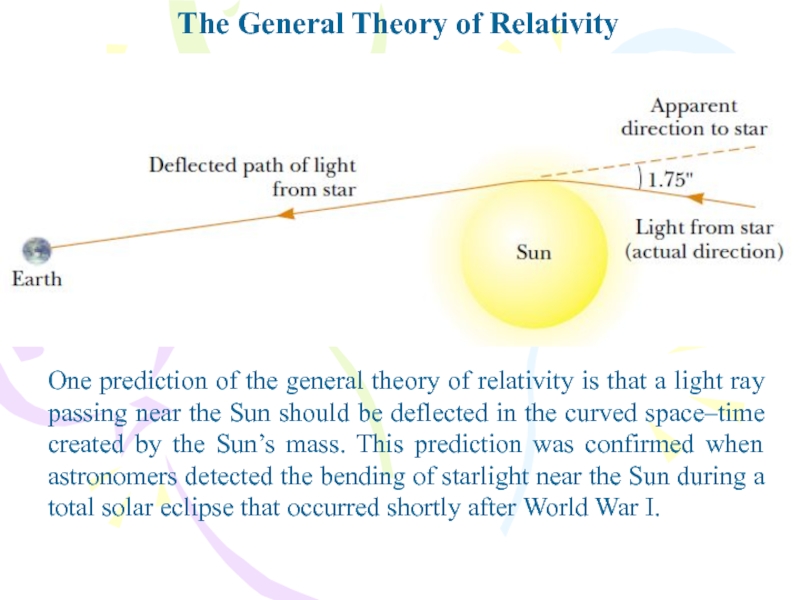
One prediction of the general theory
of relativity is that a light ray passing near the
Sun should be deflected in the curved space–time created by the Sun’s mass. This prediction was confirmed when astronomers detected the bending of starlight near the Sun during a total solar eclipse that occurred shortly after World War I.
Слайд 30Quick Quiz 1
The following pairs of energies represent the rest
energy and total energy of three different particles: particle 1:
E, 2E; particle 2: E, 3E; particle 3: 2E, 4E. Rank the particles, from greatest to least, according to their (a) mass; (b) kinetic energy; (c) speed.