Абсолютная геометрия

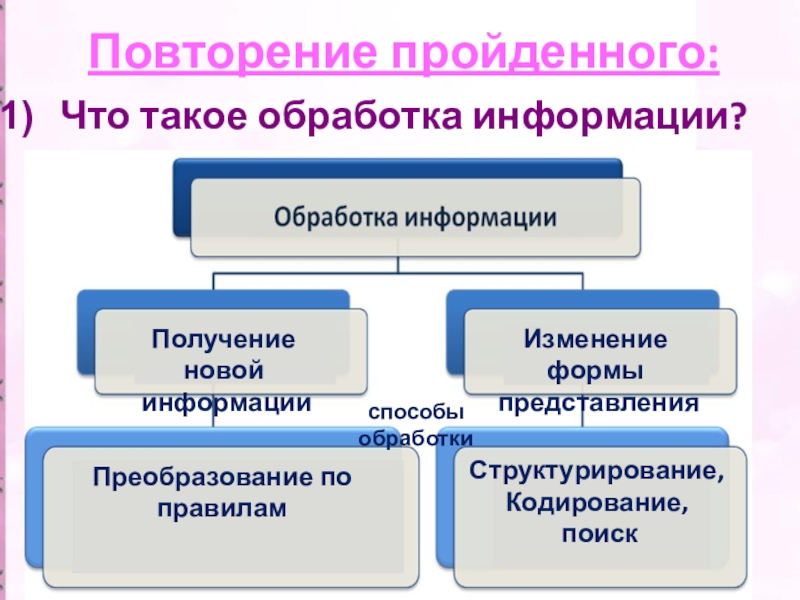
называется евклидовой геометрией.
Евклидова плоскость:

Евклидово пространство:

Определение. Геометрия четырёх

групп аксиом I-IV системы аксиом Гильберта и аксиомы параллельности Лобачевского V* называется геометрией Лобачевского.
Плоскость Лобачевского:

Пространство Лобачевского:

четырех группах аксиом системы аксиом Гильберта.
Факты абсолютной геометрии одновременно справедливы,

как в евклидовой геометрии, так и в геометрии Лобачевского.
Таким образом, все следствия, которые можно получить из групп аксиом: I,I-II,I-III,I-IV системы аксиом Гильберта, включая и теорию длин отрезков, относятся к абсолютной геометрии. Эти следствия ранее были более подробно изучены в курсе дисциплины «Основания геометрии».

оси.
Для начала вспомним, что значит установить порядок точек на

прямой. Рассмотрим прямую и некоторую точку О, принадлежащую ей. Точка О разбивает прямую на 2 луча (класса). Обозначим их – I и II.
На I луче точка М предшествует точке N, если М*ON.

На II луче точка P предшествует точке Q, если P*QO.

Все точки I класса предшествуют точкам II класса.

точку О. Каждой точке данной прямой отнесем вещественное число по

следующему правилу:
Если точка О предшествует точке М, то соответствующее число равняется длине отреза ОМ.

М → |OM|

Если точка M предшествует точке О, то число отличается знаком от длины отрезка.

Точке О сопоставляем число 0.

М → ─ |OM|

O → 0

Определение. Ось, точкам которой отнесены указанным способом вещественные числа, называется числовой осью.

числа взаимно однозначно – каждой точке соответствует число, разным точкам

соответствуют разные числа и всякое вещественное число является сопоставленным с некоторой точкой прямо
Построенное отображение сохраняет порядок, т. е. если точки М, N имеют координаты xm, xn, то точка М тогда и только тогда предшествует точке N, когда xm < xn. Это свойство прямой называется непрерывностью.
Свойство непрерывности прямой позволяет установить в абсолютной геометрии следующее предложение Дедекинда:
Если все точки направленной прямой распределены по некоторому закону на два непустых класса так, что 1) каждая точка относится к одному и только одному классу; 2) каждая точка первого класса предшествует точкам второго класса; то существует точка, которая является либо последней точкой первого класса, либо первой точкой второго класса.

две взаимно ортогональные прямые Ох и Оу пересекаются в точке

О. На каждой из них выберем положительное направление и построим числовые оси Ох, Оу.

Возьмем произвольную точку М на плоскости хОу и опустим из нее перпендикуляр ММ1 на ось Ох. Координату х точки М1 оси Ох примем за абсциссу точки М. За ординату точки М примем длину отрезка ММ1 с положительным или отрицательным знаком в зависимости от того, лежит ли

точка М и положительная полуось Оу соответственно по одну или по разные стороны относительно оси Ох.
Замечание: эта система координат не является прямоугольной декартовой, так как угол М2ММ1, вообще говоря, не прямой, он может быть прямым и острым.

углов любого треугольника в абсолютной геометрии не может быть больше

2d (двух прямых).
Дано: ∆MNK – любой.
Доказать: ∠M+∠N+∠K < 2d.
Доказательство (методом от противного).
Пусть существует в абсолютной геометрии ∆АВС, такой что ∠А+∠B+∠C > 2d.
1. Продолжим сторону АС. Построим последовательно, как показано на
рисунке, n-1 треугольник, равный данному. Таким образом, имеем:
А1А2= А2А3 = … = Аn-1Аn = AC,
А1B1= А2B2 = … = Аn-1 Bn-1,
∠B1А1Аn = ∠B2А2Аn = … = ∠Bn-1Аn-1Аn = ∠BАC .
Все треугольники равны друг другу по двум сторонам и заключенному между ними углу.

отрезки, вообще говоря, не принадлежат одной прямой.
3. По предположению

имеем:
∠A+ ∠B+ ∠C > 2d.
С другой стороны:
∠А+ ∠BСB1 + ∠С = ∠С+ ∠BСB1 + ∠ B1CА2 = 2d.
Отсюда следует, что ∠B > ∠BСB1, т.е. стороны в ∆АВС и ∆ВB1С, лежащие против указанных углов, связаны неравенством АС > ВB1.
4. Ломаная АВB1…Bn-1An больше замыкающей АAn, тогда
АВ+ВB1(n–1)+ВС > nАС.
Сгруппируем слагаемые с n: АВ - ВB1+ВС > n(АС - ВB1).
В полученном неравенстве левая часть – фиксированный отрезок АВ - ВB1+ВС, в правой – отрезок n(АС - ВB1), где n – произвольное натуральное число. Это невозможно по аксиоме Архимеда. Пришли к противоречию, следовательно предположение неверно, т.е. сумма углов любого треугольника в абсолютной геометрии не больше 2d, ч.т.д.

треугольнике на плоскости абсолютной геометрии сумма углов равна 2d, то

сумма углов любого треугольника равна 2d.
Схема доказательства (ссылка).
Для доказательства теоремы необходимо воспользоваться определением дефекта треугольника и его свойствами. (Дефектом δ(АВС) треугольника ∆АВС называют разность между развернутым углом и суммой его углов: δ(АВС) = 2d - (∠А+∠B+∠C)). Достаточно доказать, что из равенства нулю дефекта какого-либо треугольника на плоскости следует равенство нулю дефекта любого другого треугольника.
Прежде всего, доказывается это утверждение для прямоугольных треугольников. Далее рассматриваем произвольный треугольник. Если дан не прямоугольный треугольник, то его всегда можно разбить на два прямоугольных треугольника. Для этого достаточно провести высоту к его большей стороне, которая будет лежать внутри треугольника. 
Следствие. Если в одном треугольнике сумма углов меньше 2d, то сумма углов всякого треугольника меньше 2d.

то выполняется аксиома параллельности Евклида.

Дано: прямая a и точка A

∉ a, сумма углов треугольника равна 2d. Доказать: выполнение аксиомы параллельности Евклида.
Доказательство.

1. Проведем AB и a՛, такие что AB ⊥ a, a՛⊥AB, A ∈ a՛. 2. Известно, что a ⋂ a՛ = ø. Докажем, что всякая другая прямая b, проходящая через точку А, пересекает прямую а в той полуплоскости с границей АВ, которая содержит острый угол β.
3. В этой полуплоскости отложим последовательно на прямой а отрезки BB1 = AB, B1B2 = AB1, … , Bn-1Bn = ABn-1.
4. Так как сумма углов каждого треугольника равна 2d и треугольник ∆ABB1 - равнобедренный, то ∠BAB1 = ∠AB1B = d/2.

d/4 = d/22.

Продолжая далее, находим:
∠ABnB = d/2n ,
тогда

∠BABn = d - d/2n .
6. По условию β – острый (фиксированный), т.е. β < d. Можно взять такое большое n, что ∠BABn > β. Тогда получим, что прямая b проходит через вершину А треугольника ∆ABBn и пересекает его внутреннюю область. Отсюда можно заключить, что прямая b пересекает прямую а в некоторой точке, лежащей между точками B и Bn, ч.т.д.
Примечание. Аксиома Евклида: «Если сумма внутренних углов с общей стороной, образованных двумя прямыми при пересечении их третьей, с одной из сторон от секущей меньше 180°, то эти прямые пересекаются, и притом по ту же сторону от секущей».