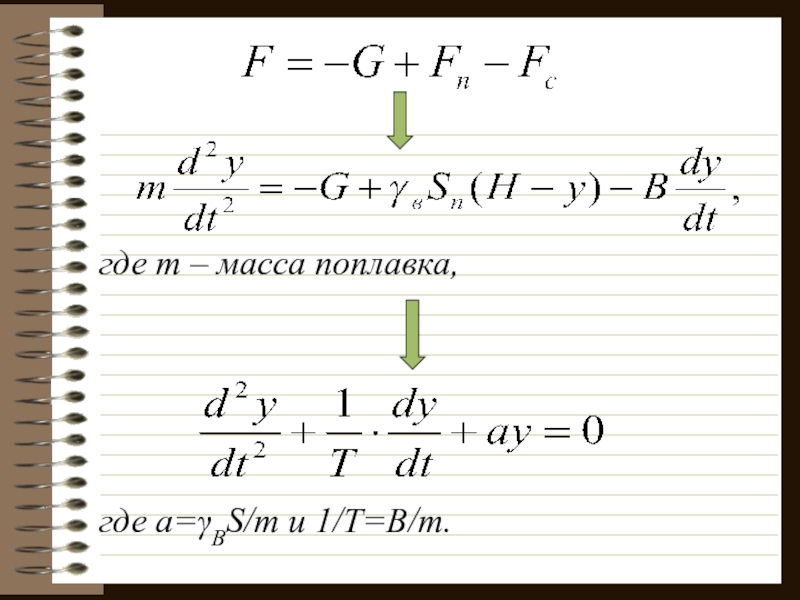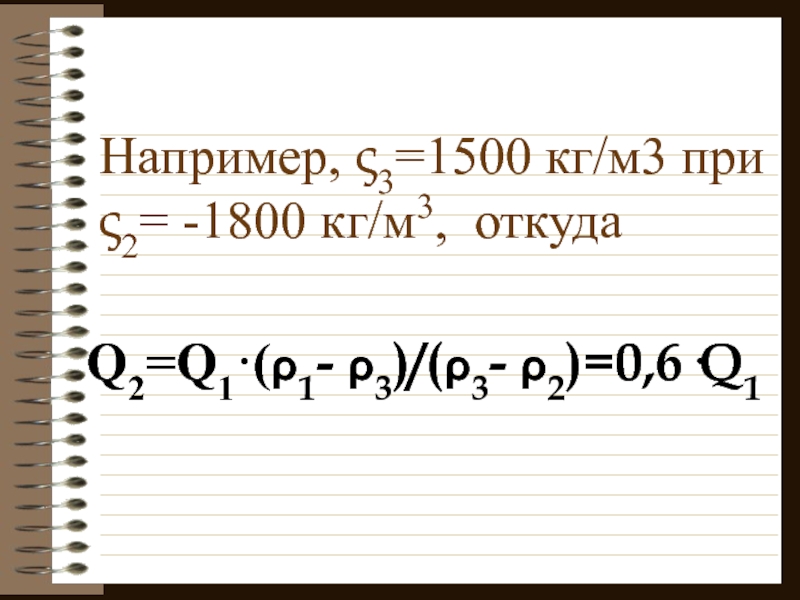Слайд 2Цель лекции.
Изложение основных понятий и методов моделирования технических процессов.
Этапы абстрактного
моделирования.
Классификация моделей по признаку наличия предварительной информации.
Методы построения моделей детерминированного
и стохастического типа.
Модели с использованием марковских цепей и иммитационные модели.
Слайд 3Физическая модель – это копия прибора, приспособления или машины, называемой
натуральной, которая подчиняется определенным правилам.
Цель моделирования – изучение определенной ситуации
для выбора оптимального решения, удовлетворяющего какому-то критерию.
Слайд 4Этапы абстрактного моделирования
Информационная модель
Логико-математическая модель
Алгоритм и программа
Исследование на ЭВМ
Интерпретация результатов,
проверка и, если необходимо, корректировка моделей и программ
Слайд 5– это конкретное словесное описание ситуации, изучаемого явления, где отвечается
на вопросы: что происходит, почему происходит и при каких условиях
происходит (при этом очень важно уточнить начальные и граничные условия ).
Информационная модель переводится на логико-математический язык .
Информационная модель
Слайд 6Перед построением математических моделей необходимо составить информационную модель.
Классификация моделей по
признаку наличия информации:
Первая группа - модели, в которых информация
отсутствует .
Вторая группа - модели, в которых информация достаточна.
Слайд 7Классификация моделей:
детерминированные, к которым относятся статические
(алгебраические) и
динамические, представляемые в виде систем дифференциальных
уравнений;
стохастические (вероятностные), когда имеем дело с массовыми явлениями.
Слайд 8Если расчет на модели дает результаты такого же порядка, как
и результаты опытных исследований, можно считать, что модель адекватна.
Слайд 9Детерминированные процессы:
Закон сохранения массы:
dV=(Q1-Q2).dt
при плотности Q1=Q2=const, dV – изменение объема
жидкости в резервуаре, Q1 и Q2 – входящий и исходящий
расход жидкости за время dt.
Слайд 10Детерминированные процессы:
2. Закон сохранения импульса силы или количества движения:
d(mV)=(ΣF).dt,
m
– масса тела, V – его скорость, ΣF – внешние
силы и dt – элементарный промежуток времени.
Слайд 11Детерминированные процессы:
3. Закон сохранения момента количества движения.
Этот закон, как и
предыдущий, находит большое применение при построении математических моделей разных явлений,
начиная от самых простых, до сложных случаев. Этот закон находит применение в расчетах турбин, компрессоров, насосов и аналогичных лопаточных устройств
Слайд 12Детерминированные процессы:
4. Закон сохранения энергии:
гидромеханика:
P – давление, γ - объемный
вес, z - высота, V - скорость потока, g
- ускорение силы тяжести.
Слайд 13Детерминированные процессы:
Термодинамика
Эп+Эк=U=const
сумма потенциальной, кинетической и внутренней энергии есть
величина постоянная.
Слайд 14Детерминированные процессы:
явления переноса:
диффузия;
внутреннее трение или вязкость;
теплопроводность.
Слайд 15Распространение молекул примеси в жидкости или газе при отсутствии
макроскопических перемещений подчиняется закону Фука
где q — поток диффундирующего
вещества; D — коэффициент диффузии;
ΔC/ΔY — градиент концентрации вещества.
Слайд 16Сила внутреннего трения равна
где η - коэффициент вязкости
Через газ,
заключенный между параллельными стенкам имеющими разные температуры Т1 и Т2
в направлении, нормальном к стенке, будет распространятся поток тепла, описываемый законом Фурье:
где λ - коэффициент теплопроводности, ΔТ — приращение температуры.
Слайд 17Многие модели в электротехнике строятся на основании закона Ома для
постоянного тока:
где i — сила тока, Е
— электродвижущая сила, г — внутреннее сопротивление источника, R — нагрузка.
Для переменного тока при наличии индуктивности L и емкости С закон Ома представим в виде:
Слайд 18Так как Q=V.C и dQ=i.dt, имеем dV/dt = i/C.
Подставляя dV/dt в уравнение и дифференцируя его, получим:
Слайд 19На основании первого закона Кирхгофа для сходящихся
в точке токов имеем Σi=0 - как выражение закона
сохранения электрического заряда.
По второму закону Кирхгофа для замкнутого контура имеем
ΣiR+ Σir= ΣE,
т.е. алгебраическая сумма произведений токов на сопротивление равна алгебраической сумме электродвижущих сил, действующих в замкнутом контуре.
Слайд 20В физике имеется группа уравнений в частных производных, известных под
названием уравнений математической физики. Уравнение теплопроводности или диффузии представим в
общем виде:
Слайд 21Явление выделения
Пусть за время dt выделяется масса dm, определяемая выражением
-dm=
p·m·dt,
где р - коэффициент пропорциональности, (1/с). Тогда
dm/m=-p·dt
Интегрируя это выражение, получаем:
lnm
= -pt + C
при t0=O, C·ln m0. Потенцируя выражение получим m=m0 ·e-pt . Если обозначить р через 1/t0, то m=m0exp(-t/t0). В безразмерном виде m=m0ехр (- τ ), где τ=t/t0 или μ=ехр(- τ).
Слайд 22Уравнение движения поплавка
Будем исходить из уравнения баланса массы.
Изменение объема воды в резервуаре за время dt равно разнице
между
входом и выходом, что можно представить в виде уравнения
S·dH = (Q - q) · dt,
где Q - приток воды, q - расход воды, S - площадь сечения резервуара, Н - высота.
Слайд 23Для короткого трубопровода справедливо соотношение:
где f(y), [м2] – функция высоты
Н. Можно предположить, что f(y)=B·y в случае прямоугольного сечения отводящей
трубы. При μ=const:
В установившемся режиме:
Слайд 24Динамические модели на основе модели поплавка
Учет колебаний воды в
трубопроводе приводит к сложному явлению «гидравлического удара».
На попловок действует
сила веса G, подъемная сила
Fn=γвSn(H-y),
А также сила вязкости сопротивления
Слайд 25
где m – масса поплавка,
где a=γВS/m и 1/T=B/m.
Слайд 26при dE/dt ≠ 0 получаем типичный вынужденный колебательный процесс
Решение
этого типа уравнений имеет вид затухающего "скачка" или затухающих колебаний
при большом сопротивлении и dE/dt=0
при dE/dt ≠ 0 получаем типичный вынужденный колебательный процесс
где
φ - угол поворота вала; Т - постоянная, учитывающая момент инерции масс (с2);
U - напряжение.
Слайд 27Вероятностные (стохастические) модели
В стохастических моделях участвуют случайные величины.
Слайд 28рассмотрим процесс осаждения группы тяжелых частиц в канале при распределенной
скорости воды, являющейся функцией глубины канала.
частицы в канале имеют нулевую
скорость в точке Х=0 и h = h0 =2м
скорость воды в канале соответствует v=(1-0,25h) · h
при h=h max=2m максимальная скорость составляет величину vmax =1м/с
Слайд 29частицы испытывают воздействия турбулентных пульсаций скорости потока fx и fy
частицы имеют скорость опускания
U= f (d)
пульсации имеют нормальное
распределение со средним значением
f х= f y= 0 и средним квадратическим отклонением Se=qv, где q - коэффициент пропорциональности.
Таким образом, величина пульсации пропорциональна скорости потока.
Слайд 30вычисляют два случайных числа, равномерно распределенных в пределах
0≤ р ≤1
вычисляют уже нормально распределенные числа при Рср=0
и σ2=1, где
σ2- дисперсия,
Рср -среднеквадратичное отклонение
Слайд 31скорости перемещения частиц будут следующими:
по высоте (вниз) — (u+fv)
по длине — (v+fx).
За время d t имеем перемещения частиц
по высоте и длине соответственно:
h = h- (u + fv) ·dt,
Х = Х+ (V+ fx ) ·dt.
Опускание частицы заканчивается при h=0. При этом отмечается расстояние х опускания частиц.
Слайд 32Численный эксперимент состоит в последовательном опускании частиц и регистрации расстояния
опускания Lx. Целью эксперимента может быть, например, изучение распределения частиц
по дну канала в зависимости от глубины, скорости воды и ее градиента по высоте, а также анализ влияния крупности частиц или пульсаций скорости потока воды на распределение частиц по высоте канала до момента опускания их на дно.
Слайд 33Пример построения математической модели с последующим усложнением
Необходимо
построить математическую модель смесителя в виде резервуара, в который
поступает тяжелая жидкость с плотностью -
ρ1 (кг/м3) и расходом Q1 ( м3/ с). Растворителем служит вода с плотностью -
ρ2 =1000 (кг/м3) и расходом Q2 (м3/ с) соответственно. Из резервуара вытекает смесь с расходом Q3 (м3/ с) при заданной плотности ρ3 (кг/м3).
Слайд 34При равновесии систем имеем уравнение баланса количества жидкости
Q1+Q2=Q3
а также уравнение баланса массы
ρ1Q1+ ρ 2Q2= ρ 3Q3
откуда
ρ 3=(Q1
ρ 1+ Q2 ρ 2)/(Q1+Q2)
Слайд 35Например, ς3=1500 кг/м3 при
ς2= -1800 кг/м3, откуда
Q2=Q1·(ρ1- ρ3)/(ρ3- ρ2)=0,6·Q1
Слайд 36В динамике также будем исходить из уравнения сохранения массы -
массового баланса за время d t.
Изменение массы в системе:
dm
= (Q1 ρ1+ Q2 ρ2- Q3 ρ)·dt
однако
dm = d (V ρ) = ρ ·dV+V·d ρ
dV = d(Fh) = h·dF+F·dh
Слайд 37Введем первое ограничение, что резервуар цилиндрический, и тогда
dV=F·dh
и dm= ρ F · dh + V ·d ρ.
Пусть
резервуар заполнен водой до уровня, при котором
Q3=Q1+Q2
следовательно
dV=0, так как V=const
Слайд 38Тогда Vd ρ = (Q1 ρ1+Q2 ρ2-Q3 ρ) dt
получаем
Решение
-1/b ·ln(a-by)=x+c
или –ln(ρ∞-ρ)=t/T+C, где
T=V/Q3
И окончательно
ρ = (ρ∞-ρ2)·e-t/T(кг/м3)
при
t=0
C= - ln(ρ∞-ρ2)
Слайд 39Рассмотрим более общую модель
dV=F·dh+h·dF=(Q1+Q2-Q3) · dt, где
При F=const, dV=F·dh
Слайд 42Марковские цепи
Для описания многих явлений, которые можно представить как
совокупность ряда состояний, в современной вычислительной математике находит применение теория
цепей Маркова. Очень эффективно эта теория используется в случае явлений, описываемых моделями с распределенными параметрами.
Слайд 43рассмотрим диффузионное осаждение тяжелых частиц в жидкости, приняв одномерную модель.
Частица, находящаяся в i -м слое, в результате случайных блужданий
может перейти за время d t в прилегающие соседние слои, один из которых расположен выше, а другой – ниже данного слоя с вероятностью соответственно Pi,i-1 и Pi,i+1 или оставаться в данном слое с вероятностью Pi,i. Первый индекс вероятностей указывает, из какого слоя переходит данная частица, а второй — в какой слой.
Слайд 44Частицы могут переходить и на более удалённые слои, то есть
Pi,i-j , …, Pi,i+1.
Слайд 45Пользуясь матричным исчислением, можно представить переход из одной временной совокупности
состояний
в совокупность состояний для момента времени
при помощи умножения вектора аt
на матрицу Р в виде
Слайд 46Например, при размерности матрицы, равной трем, имеем:
Тогда
Слайд 47Если речь идет о количестве частиц в замкнутом
резервуаре, то соблюдается закон сохранения
Слайд 48Связь между дифференциальным уравнение в частных производных параболического типа и
цепями Маркова
уравнения Фоккера-Планка:
где в общем случае A,D = const.
Слайд 49производные в виде конечных разностей
Слайд 50Конечно-разностный аналог уравнения
Слайд 52Обозначим также Рi,i=1-2c, Pi-1,i= - b+c,
Pi+1,i= - b+c
Так
как b>0 и с>0, то для устойчивости решения требуется лишь,
чтобы Рi,j ≥ 0. Отметим также, что здесь имеет место закон сохранения величины (массы, импульса и т.д.)
Расчет марковской цепи
Слайд 53Формулы вычислений имеют вид
Формы для вычисления шага интегрирования или, точнее,
дискретного шага расчета марковской цепи.
Слайд 54Имитационное моделирование
Имитационное моделирование является перспективным направлением моделирования явлений
и процессов в природе и технике. Оно возникло с
появлением ЭВМ и получит еще более широкое применение по мере развития вычислительной техники.
Слайд 55рассмотрим модель, в которой волк преследует зайца. Пусть в момент
времени t=t0
заяц находится в точке x=xz, у = 0, а волк — в точке х=хv, у = уy. Заяц может перемещаться лишь вдоль оси х с постоянной скоростью Vz.
Слайд 56Составим - дифференциальное уравнение, описывающее движение волка. Пусть за время
dt заяц переместился на dxz=Vz dt, а волк — на
Vvdt. В проекции на оси координат имеем
dx = Vvdt·sinΘ,
-dy = Vvdt·cosΘ,
где
Отсюда
Слайд 57Так как при t=0 заяц находится в начале координат, то
xz=Vz·· t. Таким образом, в качестве модели преследования имеем систему
нелинейных дифференциальных уравнений:
Слайд 58Рассмотрим теперь модель, когда заяц бежит, прыгая случайно вперед-налево с
вероятностью Р=0,40, а вперед-направо — с вероятностью Р=0,60. Его скорость
увеличивается по мере уменьшения расстояния d между преследователем и преследуемым по закону
Vv=(1-exp(-60/d))·VV0.
Vz=(1-exp (-100/d))·Vz0.
В то же время скорость волка растет по аналогичному закону






















![Абстрактное моделирование Для короткого трубопровода справедливо соотношение:где f(y), [м2] – функция высоты Н. Для короткого трубопровода справедливо соотношение:где f(y), [м2] – функция высоты Н. Можно предположить, что f(y)=B·y в случае](/img/tmb/2/154271/63b054b4a1953c6cf17c53f70302de25-800x.jpg)