Алгоритм Дейкстры

абонентов.

Введем обозначения:

D(v) – суммарная стоимость минимального пути от

источника (узел с номером 1) до получателя (узел с номером v),

l(i,j) – стоимость канала от узла i до узла j. Определена только для смежных узлов. Для несмежных равна ∞.

Это подход является алгоритмом Дейкстры для сетевой маршрутизации.

Алгоритм Дейкстры

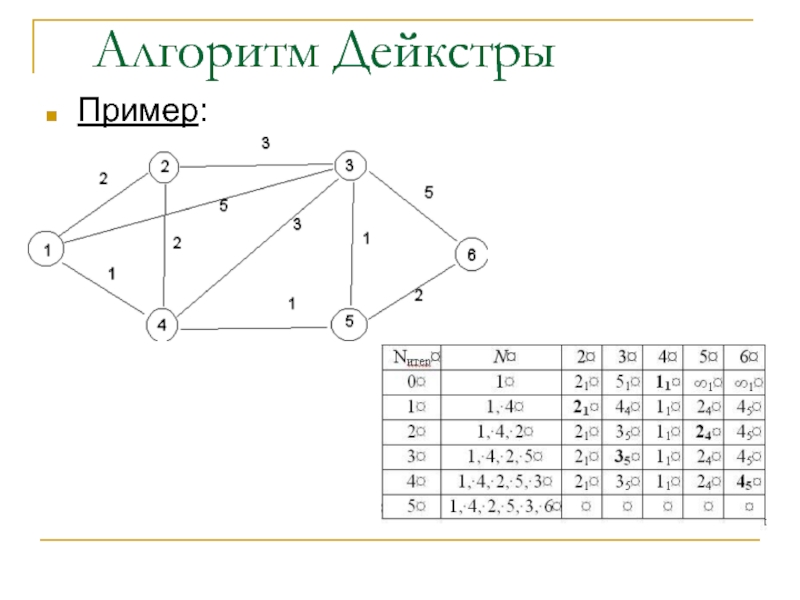
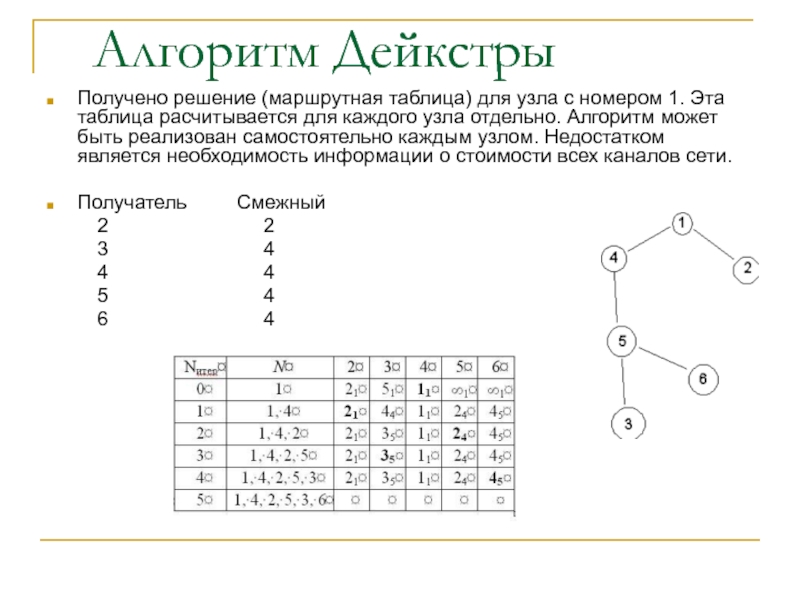
(первого). Строится таблица: строки таблицы – итерации, столбцы – номер

операции, множество N, номера узлов (начиная со второго). В строке для нулевой итерации, в столбце для узла v фиксируется значение D1(v) = l(1,v). Нижний индекс показывает номер узла, через который достигается текущее оптимальное значение. Строиться корень дерева с узлом 1.

Шаг k (k = 1,2,3,…).
В текущей строке выбираем узел v такой, что он не из множества N, но является смежным с каким-либо из узлов множества N и такой, что значение Dp(v) минимально. Узел v включается во множество N. В дереве добавляется узел с номером v в качестве потомка узла с номером p. Далее формируется новая строка таблицы, делается пересчет. Для всех узлов w∉N проверяем, изменилось ли стоимость маршрута по следующему правилу: , w* – любое, , если было оставлено старое значение, иначе.

Алгоритм заканчивает работу, исчерпав все множество вершин.

Алгоритм Дейкстры

таблица расчитывается для каждого узла отдельно. Алгоритм может быть реализован

самостоятельно каждым узлом. Недостатком является необходимость информации о стоимости всех каналов сети.

Получатель Смежный
2 2
3 4
4 4
5 4
6 4

Алгоритм Дейкстры