Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритмы на графах Тема лекции: Поиск по графу
Содержание
- 1. Алгоритмы на графах Тема лекции: Поиск по графу
- 2. 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокОбход
- 3. 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокСтруктура смежности: Множество:124356897Обход закончен!
- 4. 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокsearch
- 5. 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокProcedure
- 6. 07.04.2014Поиск на графахПОИСК В ШИРИНУ( Breadth First
- 7. 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m)
- 8. 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m)
- 9. 07.04.2014Поиск на графахПОИСК В ШИРИНУ ПримерОчередь:124356789Обход закончен!987654321
- 10. 07.04.2014Поиск на графахПОИСК В ШИРИНУ = Волновой
- 11. 07.04.2014Поиск на графахsearchDFS (vert v){ global bool
- 12. 07.04.2014Поиск на графахПОИСК В ГЛУБИНУ (ПВГ) (
- 13. 07.04.2014Поиск на графахПОИСК В ГЛУБИНУ пример
- 14. Применение ПВГПВГ с виду прост и его
- 15. 07.04.2014Поиск на графахСВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину){…setVert
- 16. 07.04.2014Поиск на графахСВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину)Рекурсивная
- 17. 07.04.2014Поиск на графахПример (нахождение связных компонент) 121234567891011111122222233Все вершины помечены. Обход закончен!
- 18. 07.04.2014Поиск на графахПример (нахождение связных компонент) 121234567891011111122222233Лес
- 19. 07.04.2014Поиск на графахСравнение с динамическим алгоритмом нахождения
- 20. 07.04.2014Поиск на графахПостроение остовного дерева и
- 21. 07.04.2014Поиск на графахпродолжение iV ++; // посетить v
- 22. 07.04.2014Поиск на графахПродолжение Собственно поиск в глубину
- 23. 07.04.2014Поиск на графахПостроение «глубинного» остовного дерева пример1234567891243567891- Номер посещения1- Номер использованияОбход закончен!
- 24. 07.04.2014Поиск на графахЗадание: Выполнить поиск в глубину
- 25. 07.04.2014Поиск на графахСвойство DFS-остова (глубинного остовного дерева)
- 26. 07.04.2014Поиск на графахИллюстрация к доказательству: {u,v} ∈
- 27. 07.04.2014Поиск на графахЗамечанияРаскраска вершинНумерация посещенных и использованных
- 28. Другая формулировка свойства DFSp[v] – номер посещаемой
- 29. Свойство DFS-остоваДля любых двух вершин u, v
- 30. 07.04.2014Поиск на графахПостроение остовного дерева пример
- 31. 07.04.2014Поиск на графахПостроение остовного дерева Единая
- 32. Замечание про прямую, обратную и противоположную теоремы
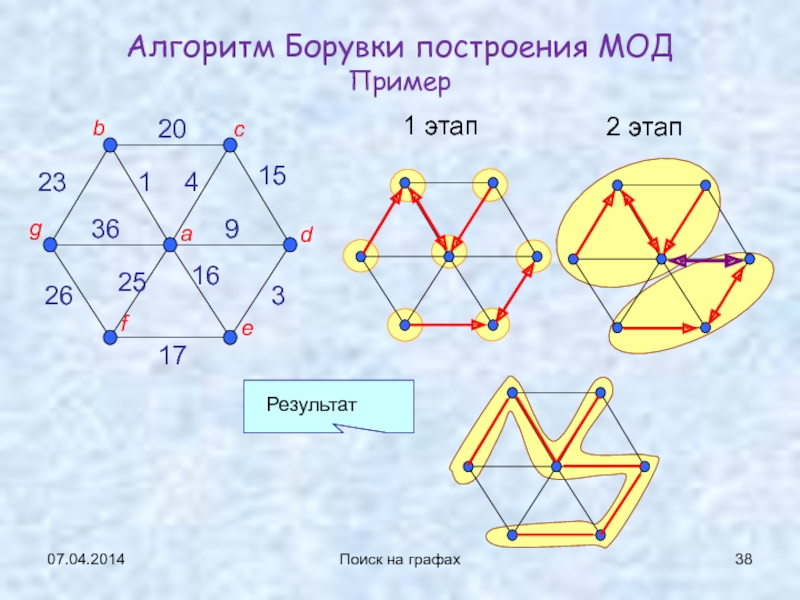
- 33. 07.04.2014Поиск на графахАлгоритм Борувки построения МОД
- 34. 07.04.2014Поиск на графахИдея алгоритмаW[a, b] = min
- 35. 07.04.2014Поиск на графахСлучай равных весов(W[b, c] =
- 36. 07.04.2014Поиск на графах{ T={ }; C={ {v1},...,{vn}
- 37. 07.04.2014Поиск на графахПродолжение (детализация)for (∀{u,v}∈E) { пусть i
- 38. 07.04.2014Поиск на графахАлгоритм Борувки построения МОД Пример1 этап2 этапРезультат
- 39. 07.04.2014Поиск на графахСложность алгоритмаНа каждом новом этапе
- 40. 07.04.2014Поиск на графахКОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 41. Скачать презентанцию
Слайды и текст этой презентации
Слайд 107.04.2014
Поиск на графах
Построение и анализ алгоритмов
Лекция 8
Раздел: Алгоритмы на графах
Тема
лекции:
Слайд 207.04.2014
Поиск на графах
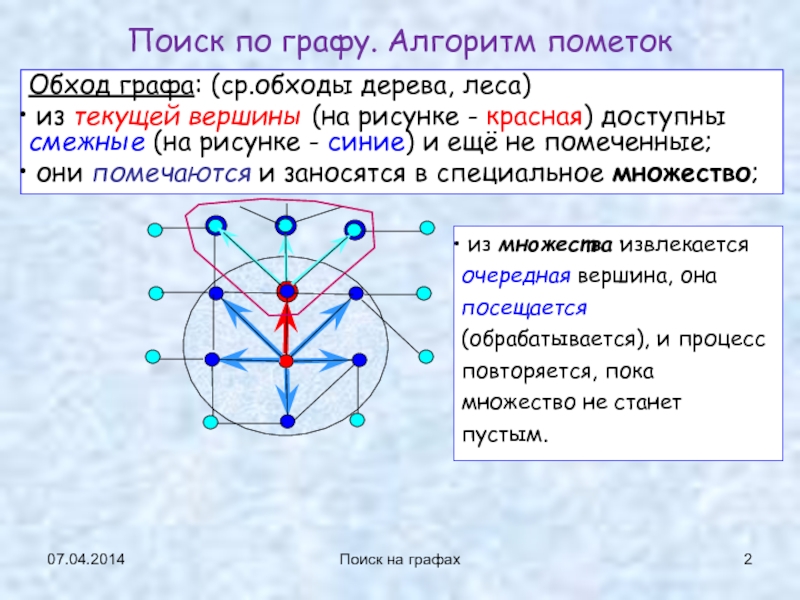
Поиск по графу. Алгоритм пометок
Обход графа: (ср.обходы дерева,
леса)
из текущей вершины (на рисунке - красная) доступны смежные
(на рисунке - синие) и ещё не помеченные;они помечаются и заносятся в специальное множество;
из множества извлекается очередная вершина, она посещается (обрабатывается), и процесс повторяется, пока множество не станет пустым.
Слайд 307.04.2014
Поиск на графах
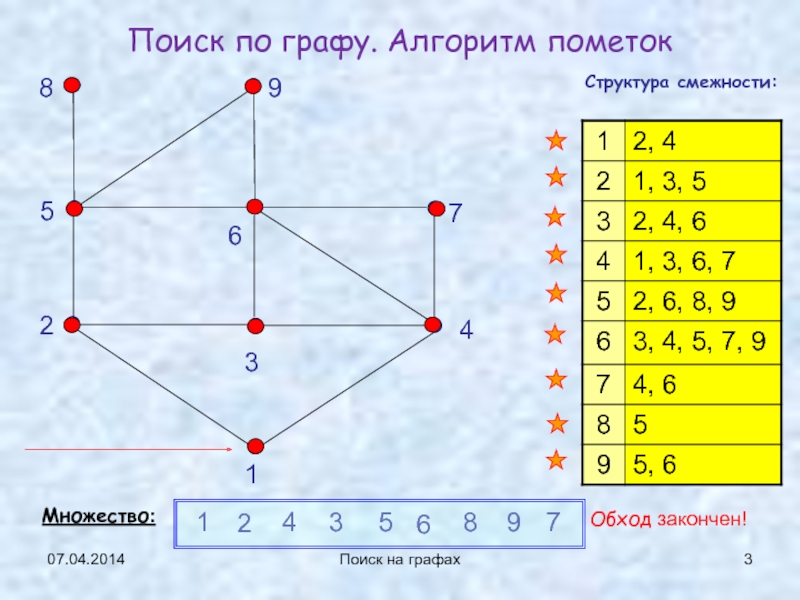
Поиск по графу. Алгоритм пометок
Структура смежности:
Множество:
1
2
4
3
5
6
8
9
7
Обход закончен!
Слайд 407.04.2014
Поиск на графах
Поиск по графу. Алгоритм пометок
search (vert v0)
{ setVert Q;
// рабочее множество вершин графа
bool newVert [n];
global setVert V; //множество вершин
графа G=(V,E), Card(V)=nlistVert adj [n]; //списки смежности
for (∀v∈V) newVert[v] = true; //пометить вершины как необследованные
Q = { v0 }; NewVert[v0] = false;
while (Q ≠ { }) {
v = произвольный элемент из Q;
удалить v из Q;
посетить ( v );
for (∀ u ∈ Adj[v]) {
if (NewVert[u]) {
Q = Q + {u};
NewVert[u] = false;
} // if
}//for
// вершина v - использована
} //while
} //search
O(n + m)
каждая вершина один раз заносится в множество и один раз исключается
Каждое ребро при анализе пометки проверяется дважды
Слайд 507.04.2014
Поиск на графах
Поиск по графу. Алгоритм пометок
Procedure Search ( v0:
Vert );
var Q : SetVert;
NewVert : Array [1..n] of
Boolean;global V : SetVert; {множество вершин графа G=(V,E), Card(V)=n }
Adj: array [1..n] of ListVert; { списки смежности }
begin
for ∀ v ∈ V do NewVert[v] := True; { - пометить все вершины как необследованные }
Q := { v0 }; NewVert[v0] := False;
While Q ≠ { } do
begin
v := произвольный элемент из Q; удалить v из Q;
посетить ( v );
for ∀ u ∈ Adj[v] do
if NewVert[u] then
begin
Q := Q + {u}; NewVert[u] := False
end {if-for}
{ вершина v - использована }
end {while}
end { Search }
O(n + m)
каждая вершина один раз заносится в множество и один раз исключается
Каждое ребро при анализе пометки проверяется дважды
Слайд 6
07.04.2014
Поиск на графах
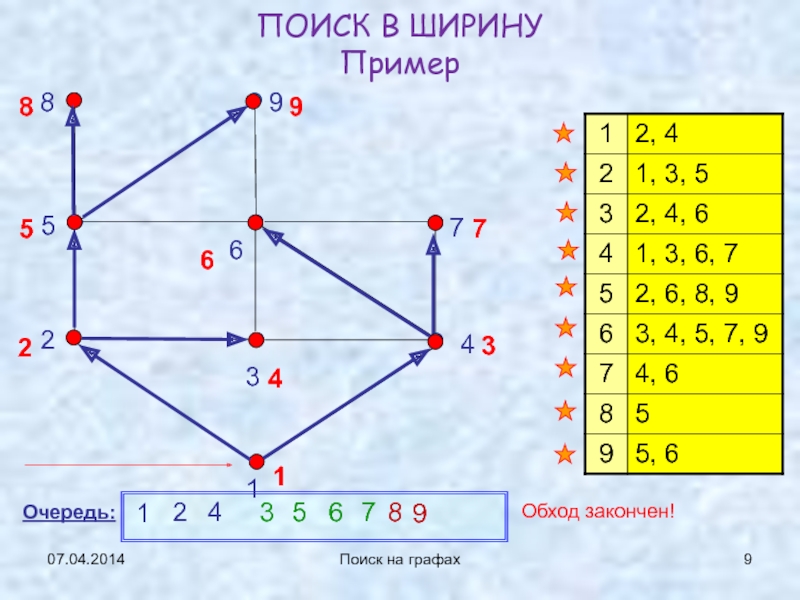
ПОИСК В ШИРИНУ
( Breadth First Search - BFS
)
Множество Q реализуется очередью q (раньше посетили - раньше использовали).
Заодно
строится остовное дерево (T – множество древесных ребер)search_BFS (vert v0)
{ queueVert q;
bool newVert [n];
global setVert V; //множество вершин графа G=(V,E), Card(V)=n
listVert adj [n]; //списки смежности
setBr T; // множество ветвей (branch) дерева
Слайд 707.04.2014
Поиск на графах
ПОИСК В ШИРИНУ ( O(n+m) )
for (∀v∈V) newVert[v]=true;//пометить
вершины как необследованные
Create(q);
q ← v0;
newVert[v0] =false;
T =
{ };while ( !Null( q )) {
v ← q;
посетить ( v );
for (∀u∈Adj[v] ) {
if (newVert[u] ) {
q ← u;
newVert[u] =false;
T = T + {
// predVert[u] = v
} //if
} //for вершина v - использована
} //while
} // searchBFS
Слайд 807.04.2014
Поиск на графах
ПОИСК В ШИРИНУ ( O(n+m) )
begin
for ∀ v
∈ V do NewVert[v] := True;
{ - пометить все
вершины как необследованные }Create(q); q ← v0;
NewVert[v0] := False; T := { };
While not Null( q ) do
begin
v ← q; посетить ( v );
for ∀ u ∈ Adj[v] do
if NewVert[u] then
begin
q ← u; NewVert[u] := False;
T := T + {
{ PredVert[u] := v }
end {if-for}
{ вершина v - использована }
end {while}
end { BFS }
Слайд 1007.04.2014
Поиск на графах
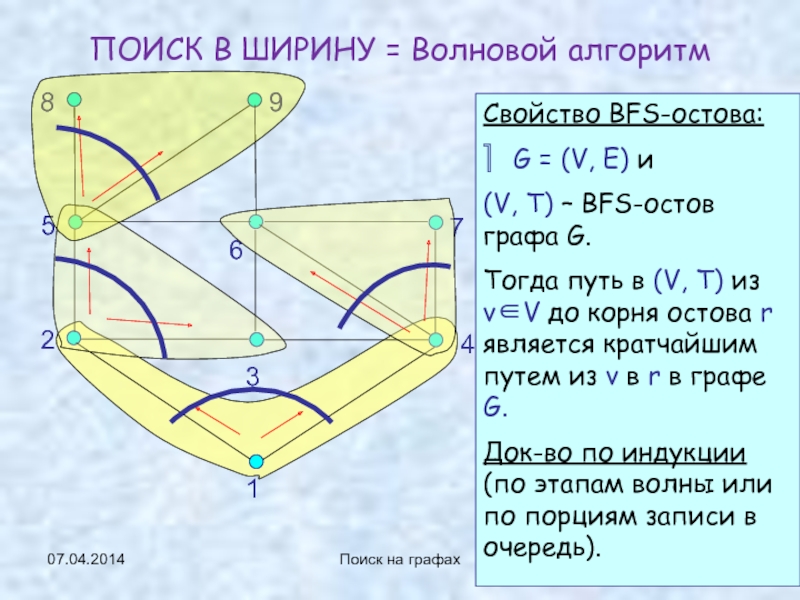
ПОИСК В ШИРИНУ = Волновой алгоритм
Свойство BFS-остова:
⎤ G
= (V, E) и
(V, T) – BFS-остов графа G.
Тогда путь
в (V, T) из v∈V до корня остова r является кратчайшим путем из v в r в графе G.Док-во по индукции (по этапам волны или по порциям записи в очередь).
Слайд 1107.04.2014
Поиск на графах
searchDFS (vert v)
{ global bool newVert [n];
setVert V;
//множество вершин графа G=(V,E), Card(V)=n
listVert adj [n];
//списки смежностиsetBr T; // множество ветвей (branch) дерева
посетить v;
newVert[v] =false;
for (∀u∈Adj[v] )
if (newVert[u]) searchDFS(u);
//v - использована
} // searchDFS
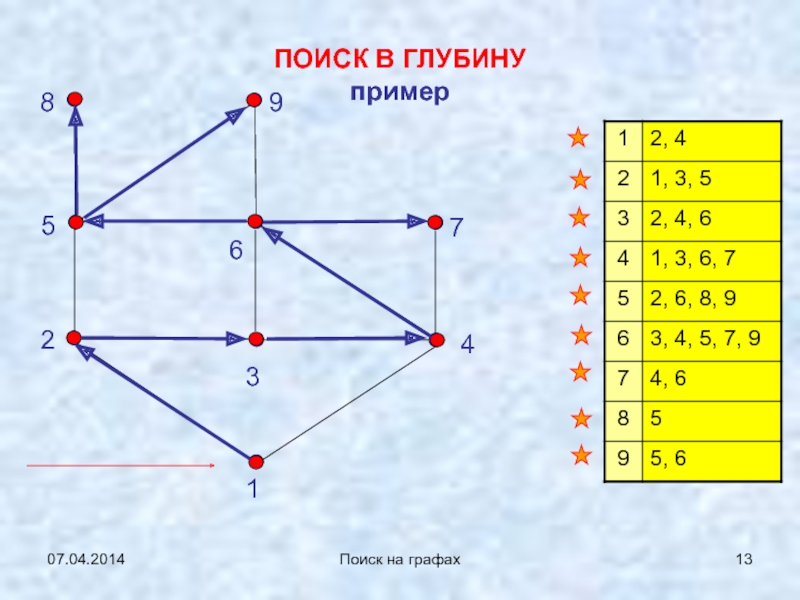
ПОИСК В ГЛУБИНУ
( Depth First Search - DFS )
Q = Stack. Можно сразу рекурсивно.
Слайд 1207.04.2014
Поиск на графах
ПОИСК В ГЛУБИНУ (ПВГ)
( Depth First Search -
DFS )
// cобственно поиск в глубину в графе G=(V,E)
{…
setVert V;
//множество вершин графа G=(V,E), Card(V)=nlistVert adj [n]; //списки смежности
for (∀v∈V) newVert[v] = true;
// - пометить все вершины как необследованные
for (∀v∈V)
if (newVert[v] ) searchDFS(v);
}
Слайд 14Применение ПВГ
ПВГ с виду прост и его несложно реализовать
На самом
деле это очень гибкий и мощный алгоритм (схема), который можно
применять для решения многих трудных задач обработки графов(Седжвик)
07.04.2014
Поиск на графах
Слайд 1507.04.2014
Поиск на графах
СВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину)
{…
setVert V; //множество вершин
графа G=(V,E), Card(V)=n }
int numComp [n1];
//вершина помечается номером своей
связной компонентыint iC ; //номер связной компоненты
for (∀v∈V) numComp[v] = 0;
// - пометить все вершины как необследованные
iC = 0;
for (∀v∈V)
if (numComp[v] == 0) {
iC++;
comp(v);
} //if
} // for
}
Слайд 1607.04.2014
Поиск на графах
СВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину)
Рекурсивная процедура (функция)
нахождения
связных компонент графа
comp (vert v)
{global int numComp [n1];
listVert adj
[n]; //списки смежностиiC : Num; //номер связной компоненты
numComp[v] = iC;
for (∀u∈Adj[v])
if (numComp[u] == 0) comp(u);
// v - использована
} //comp
Слайд 1707.04.2014
Поиск на графах
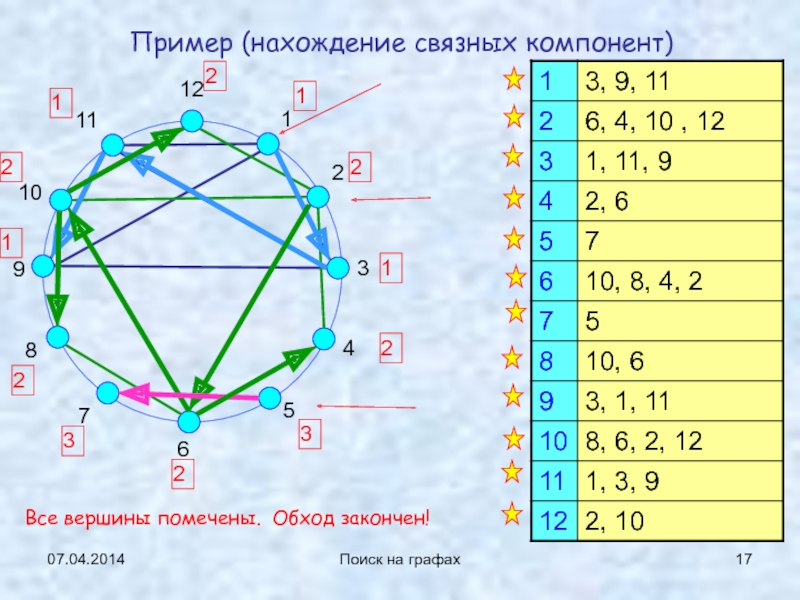
Пример (нахождение связных компонент)
12
1
2
3
4
5
6
7
8
9
10
11
1
1
1
1
2
2
2
2
2
2
3
3
Все вершины помечены. Обход
закончен!
Слайд 1807.04.2014
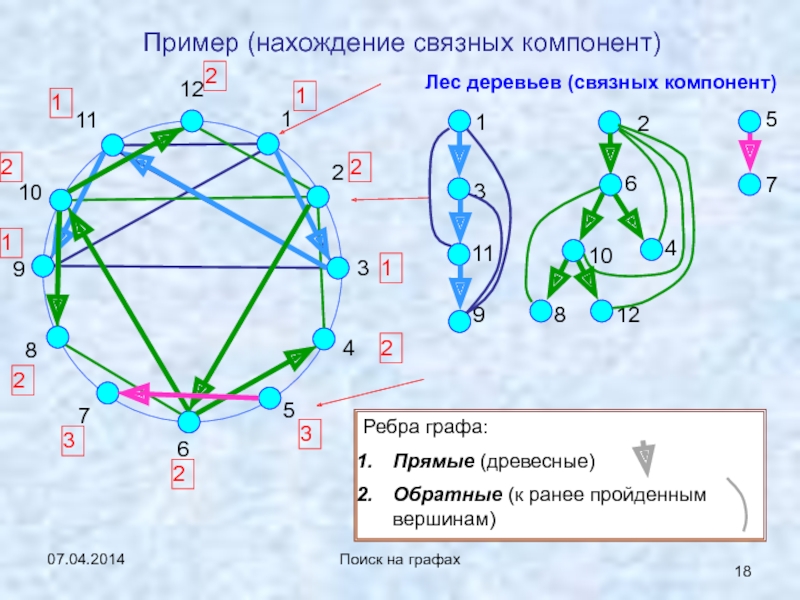
Поиск на графах
Пример (нахождение связных компонент)
12
1
2
3
4
5
6
7
8
9
10
11
1
1
1
1
2
2
2
2
2
2
3
3
Лес деревьев (связных компонент)
1
3
11
9
2
6
10
8
12
4
5
7
Ребра
графа:
Прямые (древесные)
Обратные (к ранее пройденным вершинам)
Слайд 1907.04.2014
Поиск на графах
Сравнение с динамическим алгоритмом нахождения связных компонент
Алгоритм из
лекции 5, решающий задачу связности, тоже строит связные компоненты
Алгоритм DFS-ПВГ
сложности O (n +m) эффективнее.Динамический алгоритм эффективнее в ситуации, когда ребра графа добавляются последовательно, т.к. не требует заново применять ПВГ.
Слайд 2007.04.2014
Поиск на графах
Построение остовного дерева
и множества обратных ребер
при
поиске в глубину
( Tree of Depth First Search -TDFS )
treeDFS
(vert v, vert u){ // посещаем вершину v и т.д.; u = Отец(v)
global
int numVert [n];
listVert Adj [n]; // списки смежности
int iV; /*текущий порядковый номер посещения вершины*/
setBrT; // множество ветвей остовного дерева
setBr B; // множество хорд (обратных ребер)
Слайд 2107.04.2014
Поиск на графах
продолжение
iV ++; // посетить v
numVert[v] =
iV;
for (∀w∈Adj[v]) {
if (numVert[w]==0) {
// -
ребро (ветвь) остовного дереваT = T + {
treeDFS( w, v);
}
else // w - уже посещалась
if ((numVert[w] < NumVert[v]) && (w!=u))
//
B = B + {
}// v - использована }
}// treeDFS
Слайд 2207.04.2014
Поиск на графах
Продолжение
Собственно поиск в глубину в графе G=(V,E):
{ setVert
V; //множество вершин графа G=(V,E), Card(V)=n
int numVert [n];
listVert Adj [n]; // списки смежностиint iV; //текущий порядковый номер посещения вершины setBrT; // множество ветвей остовного дерева
setBr B; // множество хорд (обратных ребер)
for (∀v∈V) numVert[v] = 0;
// - пометить все вершины как необследованные
iV = 0;
T = { }; B = { };
for (∀v∈V)
if (numVert[v]==0) treeDFS(v, v );
}
Слайд 2307.04.2014
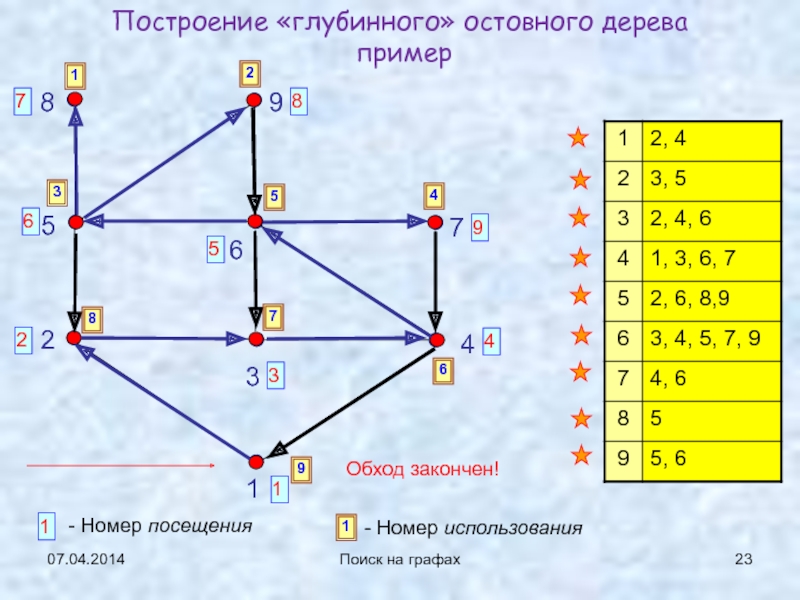
Поиск на графах
Построение «глубинного» остовного дерева
пример
1
2
3
4
5
6
7
8
9
1
2
4
3
5
6
7
8
9
1
- Номер посещения
1
- Номер
использования
Обход закончен!
Слайд 2407.04.2014
Поиск на графах
Задание:
Выполнить поиск в глубину для этого же
графа, в т. ч. построить остов и обратные ребра:
Начиная
с любой другой вершиныИзменив списки смежности (порядок элементов в списке)
Построение «глубинного» остовного дерева
пример
Слайд 2507.04.2014
Поиск на графах
Свойство DFS-остова (глубинного остовного дерева)
Пусть (V, T)
– DFS-остов графа G = (V, E) и пусть {u,
v} ∈ E. Тогда либо u потомок v (в дереве), либо v потомок u.Доказательство.
Пусть v посещена раньше, чем u. По завершении treeDFS(v) будет numVert[v] < numVert[u], т.к. {u,v} ∈ E. Но это значит, что в TDFS добавились ребра, содержащие путь из v в u. Отсюда следует, что v лежит на пути от корня в u, т.е. u потомок v.
Аналогично рассуждаем в случае, если u посещена раньше, чем v.
Слайд 2607.04.2014
Поиск на графах
Иллюстрация к доказательству:
{u,v} ∈ E
v посещена
раньше, чем u
numVert[v] < numVert[u]
r – корень TDFS
v
u
r
Свойство
TDFS-остова
(глубинного остовного дерева) Слайд 28Другая формулировка свойства DFS
p[v] – номер посещаемой (обрабатываемой – process)
вершины
f[v] - номер использованной (завершенной – finish) вершины
t – такт
времени (шаг алгоритма)Единая нумерация:
t++; p[v] = t;
…
t++; f[v] = t;
07.04.2014
Поиск на графах
Слайд 29Свойство DFS-остова
Для любых двух вершин u, v выполняется ровно одно
из трех утверждений:
Отрезки [p[u],f[u]] и [p[v],f[v]] не пересекаются, и ни
u не является потомком v в DFS-лесу, ни v не является потомком u.Отрезок [p[u],f[u]] полностью содержится в отрезке [p[v],f[v]], и u является потомком v в DFS-дереве.
Отрезок [p[v],f[v]] полностью содержится в отрезке [p[u],f[u]], и v является потомком u в DFS-дереве.
================================================
v - потомок u , ттогда, когда p[u] < p[v] < f[v] < f[u]
07.04.2014
Поиск на графах
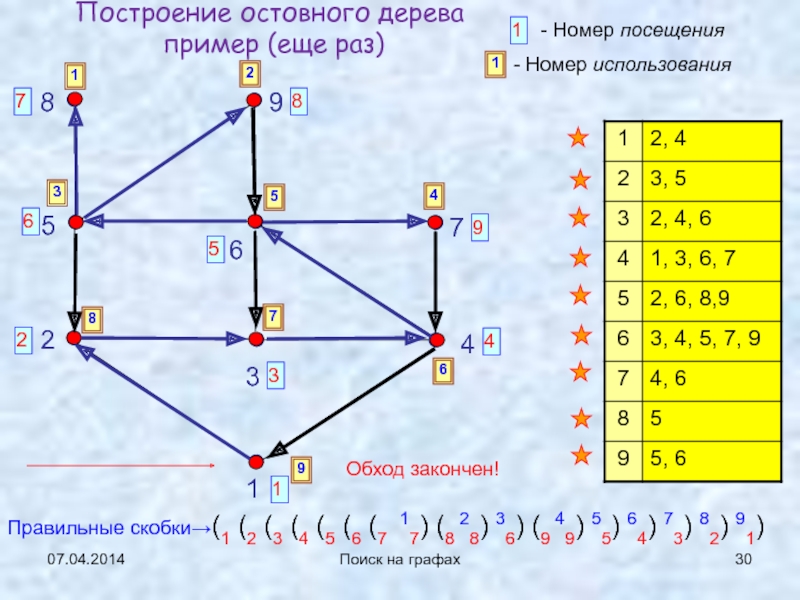
Слайд 3007.04.2014
Поиск на графах
Построение остовного дерева
пример (еще раз)
1
2
3
4
5
6
7
8
9
1
2
4
3
5
6
7
8
9
Обход закончен!
Правильные скобки→(1
(2 (3 (4 (5 (6 (7 17) (8 28) 36)
(9 49) 55) 64) 73) 82) 91)Слайд 3107.04.2014
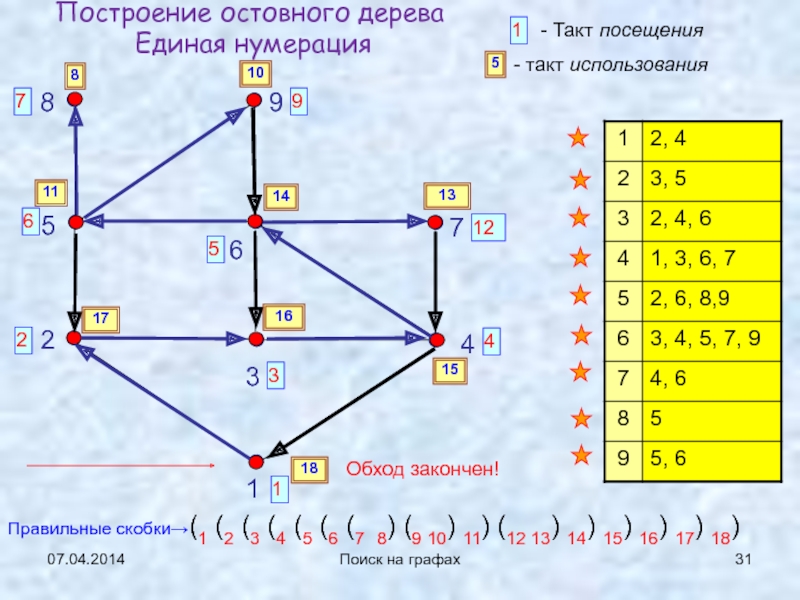
Поиск на графах
Построение остовного дерева
Единая нумерация
1
2
3
4
5
6
7
9
12
8
10
13
11
14
15
16
17
18
Обход закончен!
Правильные скобки→(1 (2
(3 (4 (5 (6 (7 8) (9 10) 11) (12
13) 14) 15) 16) 17) 18)Слайд 32Замечание про прямую, обратную и противоположную теоремы (свойство ПВГ-дерева)
07.04.2014
Поиск на
графах
A ⇒ B
Пусть (V, T) – DFS-остов графа G =
(V, E). Пусть {u, v} ∈ E. Тогда либо u потомок v (в дереве), либо v потомок u.? B ⇒ A
Пусть (V, T) – DFS-остов графа G = (V, E). Пусть либо u потомок v (в дереве), либо v потомок u. Тогда {u, v} ∈ E
? ¬A ⇒ ¬B
Пусть (V, T) – DFS-остов графа G = (V, E). Пусть {u, v} ∉ E. Тогда ни u не есть потомок v (в дереве), ни v не есть потомок u.
¬B ⇒ ¬A
Слайд 3307.04.2014
Поиск на графах
Алгоритм Борувки построения МОД
O(m*log n)
Вход :
V - множество вершин заданного графа G=(V,E)
E - множество ребер заданного графа G=(V,E)
D [1..n,1..n] - матрица весов (или ф-ия D(.,.) )
Выход: T - множество ребер МОД
Рабочие: C - множество связных компонент графа (V,T), т.е. леса;
C = {S1,...,Sk}, где Sj – связная компонента леса, т.е. дерево
Кратч[1..n] – массив ребер; Кратч[i] - ребро, кратчайшее из всех ребер, имеющих ровно один конец (вершину) в дереве (в связной компоненте) Si=(Vi,Ti);
Min[1..n] - вспомогательный массив для определения Кратч[i]
Слайд 3407.04.2014
Поиск на графах
Идея алгоритма
W[a, b] = min {W[u, v]: u∈V(a),
v∉V(a)}
W[b, c] = min {W[u, v]: u∈V(b), v∉V(b)}
W[c, a]
= min {W[u, v]: u∈V(c), v∉V(c)}(W[b, c] < W[a, b]) &
(W[c, a] < W[b, c]) →
(W[c, a] < W[a, b]) !?!?
Это в случае, когда все веса различны
Пусть правильно построен некоторый остовный лес.
Находим Кратч[i] для всех поддеревьев и добавляем их.
Определяем получившиеся связные компоненты.
Итерацию повторяем.
Слайд 3507.04.2014
Поиск на графах
Случай равных весов
(W[b, c] = W[a, b]) &
(W[c,
a] = W[b, c]) & (W[c, a] = W[a, b])
Цикл !?!?Разрыв цикла
При выборе минимума в случае равных весов выбирать ребро, соединяющее с компонентой, имеющей меньший номер.
Например, a < b < c.
Тогда компонента с максимальным номером (c) не будет выбрана (при равных весах)
Слайд 3607.04.2014
Поиск на графах
{
T={ }; C={ {v1},...,{vn} };
while (Card(C)1)
{
// этап:
for (∀Si∈C) min[i]=+∞;
Для ∀Si∈C
найти Кратч[i] – кратч. из всех ребер, имеющих ровно один конец в дереве Si=(Vi,Ti) /*см. след.сл.*/for (∀Si∈C) T = T + { Кратч[i] } ;
Найти множество C связных компонент графа (V,T);
} //while
/*Примечание: если при нахождении связных компонент вычислен массив numComp[ ] (см.сл.13-14),
то i и j, используемые далее, определяются так:
i =numComp[u]; j =numComp[v] */
}
Детализировано на следующем слайде
Слайд 3707.04.2014
Поиск на графах
Продолжение (детализация)
for (∀{u,v}∈E) {
пусть i и j такие,
что (u ∈ Si) & (v ∈ Sj);
if
(i!=j) {if (d(u,v) < min[i]) {
min[i] = d(u,v);
Кратч[i] ={u,v};
};
if (d(u,v) < min[j] ) {
min[j] := d(u,v);
Кратч[j] := {u,v};
};
} // if (i!=j)
} // for
Слайд 3907.04.2014
Поиск на графах
Сложность алгоритма
На каждом новом этапе число деревьев уменьшается
не менее, чем вдвое (!).
Т. о. всего не более чем
log2 n этапов.Каждый этап имеет стоимость O(m).
Общая сложность O(m log2 n ).

![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокsearch (vert v0){ setVert Q; // 07.04.2014Поиск на графахПоиск по графу. Алгоритм пометокsearch (vert v0){ setVert Q; // рабочее множество вершин графа bool newVert [n]; global setVert](/img/thumbs/a161655b6097c5247d43af857f5471cd-800x.jpg)


![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m) )for (∀v∈V) newVert[v]=true;//пометить вершины 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m) )for (∀v∈V) newVert[v]=true;//пометить вершины как необследованные Create(q); q ← v0; newVert[v0]](/img/thumbs/b27128b959937ce0eb972d754f980a84-800x.jpg)
![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m) )begin for ∀ v ∈ 07.04.2014Поиск на графахПОИСК В ШИРИНУ ( O(n+m) )begin for ∀ v ∈ V do NewVert[v] := True; {](/img/thumbs/775ab7d5b1a241c07cf1947b57fcd06b-800x.jpg)
![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахsearchDFS (vert v){ global bool newVert [n]; setVert V; //множество 07.04.2014Поиск на графахsearchDFS (vert v){ global bool newVert [n]; setVert V; //множество вершин графа G=(V,E), Card(V)=n](/img/thumbs/3bca13c703eba2e90b1ac2cf9abea7d5-800x.jpg)


![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахСВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину){…setVert V; //множество вершин графа 07.04.2014Поиск на графахСВЯЗНЫЕ КОМПОНЕНТЫ (Поиск в глубину){…setVert V; //множество вершин графа G=(V,E), Card(V)=n }int numComp [n1]; //вершина](/img/thumbs/3cbc8d4e098bb69b63b1968fa088153a-800x.jpg)



![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахпродолжение iV ++; // посетить v numVert[v] = iV; for 07.04.2014Поиск на графахпродолжение iV ++; // посетить v numVert[v] = iV; for (∀w∈Adj[v]) { if (numVert[w]==0)](/img/thumbs/54b922e68edbd237e403a5008e8e89e7-800x.jpg)



![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахИллюстрация к доказательству: {u,v} ∈ E v посещена раньше, 07.04.2014Поиск на графахИллюстрация к доказательству: {u,v} ∈ E v посещена раньше, чем u numVert[v] < numVert[u] r](/img/thumbs/eb0b896e1bc5b6cbbd6491f8e489c927-800x.jpg)

![Алгоритмы на графах Тема лекции: Поиск по графу Другая формулировка свойства DFSp[v] – номер посещаемой (обрабатываемой – process) вершиныf[v] Другая формулировка свойства DFSp[v] – номер посещаемой (обрабатываемой – process) вершиныf[v] - номер использованной (завершенной – finish)](/img/thumbs/d08438359ee6029dd542807f69d31137-800x.jpg)
![Алгоритмы на графах Тема лекции: Поиск по графу Свойство DFS-остоваДля любых двух вершин u, v выполняется ровно одно из Свойство DFS-остоваДля любых двух вершин u, v выполняется ровно одно из трех утверждений:Отрезки [p[u],f[u]] и [p[v],f[v]] не](/img/thumbs/6d8ae4732afe941ecfe8a5e0ba0ba4b9-800x.jpg)


![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахИдея алгоритмаW[a, b] = min {W[u, v]: u∈V(a), v∉V(a)} 07.04.2014Поиск на графахИдея алгоритмаW[a, b] = min {W[u, v]: u∈V(a), v∉V(a)} W[b, c] = min {W[u, v]:](/img/thumbs/f627ee7dbefde7fbf60827038c1accbe-800x.jpg)
![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графахСлучай равных весов(W[b, c] = W[a, b]) &(W[c, a] 07.04.2014Поиск на графахСлучай равных весов(W[b, c] = W[a, b]) &(W[c, a] = W[b, c]) & (W[c, a]](/img/thumbs/4650dd0e61bc0077fcdde7533a05ea44-800x.jpg)
![Алгоритмы на графах Тема лекции: Поиск по графу 07.04.2014Поиск на графах{ T={ }; C={ {v1},...,{vn} }; while (Card(C)1) { 07.04.2014Поиск на графах{ T={ }; C={ {v1},...,{vn} }; while (Card(C)1) { // этап: for (∀Si∈C) min[i]=+∞;](/img/thumbs/85b90bb7ecbf426954947f24532ada60-800x.jpg)