Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Аналитические вычисления в Matlab
Содержание
- 1. Аналитические вычисления в Matlab
- 2. Для проведения аналитических (символьных) операций нужно, чтобы соответствующие переменные были предварительно объявлены.
- 3. Упрощение выражений
- 4. Раскрытие скобок
- 5. Вычисление интегралова) вычисление неопределенных интегралов
- 6. Примеры. Вычислить неопределенный интеграл
- 7. Вычисление определенных интегралов Для вычисления определенных интегралов в
- 8. Примеры: Вычислить определенный интеграл
- 9. Вычисление двойных интегралов
- 10. Вычисление тройных интегралов
- 11. Методы приближенного вычисления интегралов
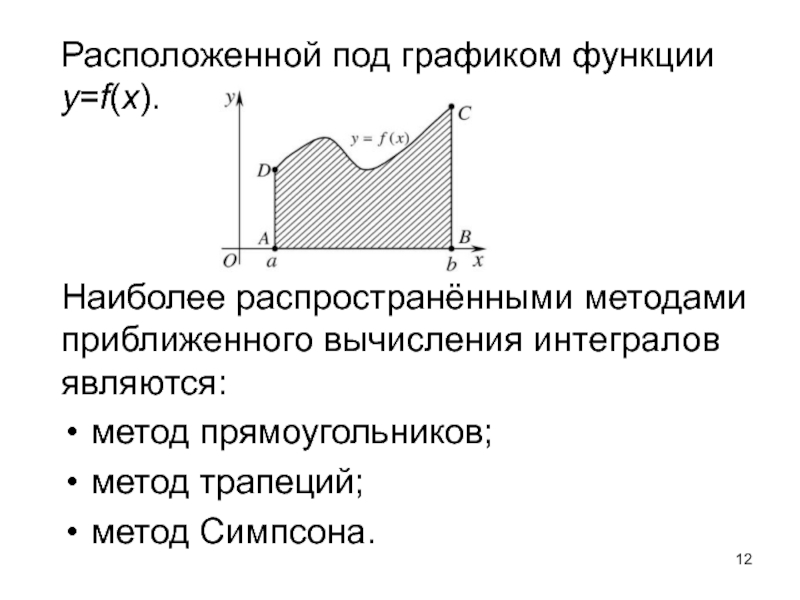
- 12. Расположенной под графиком функции y=f(x). Наиболее распространёнными методами приближенного вычисления интегралов являются:метод прямоугольников;метод трапеций;метод Симпсона.
- 13. Решение уравнений Для решения алгебраических и трансцендентных
- 14. ПримерыЕдинственное решение Решить уравнение x+2=0.
- 15.
- 16. Уравнение с комплексными корнями
- 17. Решение систем линейных алгебраических уравнений Для
- 18. то для нахождения неизвестного вектора-столбца х достаточно
- 19.
- 20. Слайд 20
- 21. Вместо знака обратной косой черты можно использовать функцию mldividex=mldivide(A,b)Результат будет тем же самым.
- 22. Функция solve() позволяет решить систему уравнений. Например,
- 23. Символьное решение дифференциальных уравнений Для
- 24. Символ D в строке уравнения обозначает дифференцирование по независимой переменной
- 25.
- 26. Слайд 26
- 27. Вычисление пределов
- 28. Слайд 28
- 29. Вычисление производных Для вычисления производных в
- 30.
- 31.
- 32. Если вторым аргументом указана переменная, то производная будет вычислена по заданной переменной.
- 33. Функция diff() может получать три
- 34. Вычисление смешанной производной
- 35. Скачать презентанцию
Для проведения аналитических (символьных) операций нужно, чтобы соответствующие переменные были предварительно объявлены.
Слайды и текст этой презентации
Слайд 2 Для проведения аналитических (символьных) операций нужно, чтобы
соответствующие переменные были предварительно объявлены.
Слайд 5Вычисление интегралов
а) вычисление неопределенных
интегралов
Для нахождения неопределенных
интегралов в символьном виде используется функция int, имеющая следующий синтаксис:
Int(f,x),
где
f – подынтегральная функция;х – переменная интегрирования.
Слайд 7Вычисление определенных интегралов
Для вычисления определенных интегралов в символьном виде используется
функция int, имеющая следующий синтаксис:
Int(f,x,a,b),
где f – подынтегральная функция;
х – переменная интегрирования;a – нижний предел интегрирования;
b – верхний предел интегрирования.
Слайд 12Расположенной под графиком функции y=f(x).
Наиболее распространёнными методами приближенного
вычисления интегралов являются:
метод прямоугольников;
метод трапеций;
метод Симпсона.
Слайд 13Решение уравнений
Для решения алгебраических и трансцендентных уравнений используется функция
solve(e1,e2,…,en),
здесь
е1, е2, …, еn –символьные выражения
или переменные.Слайд 17Решение систем линейных алгебраических уравнений
Для решения систем линейных
алгебраических уравнений используется знак \ (деление слева).
Например, если
требуется решить систему линейных уравнений Ах=b,где А – квадратная матрица размера
nxn;
b – заданный вектор-столбец
размера n,
Слайд 18то для нахождения неизвестного вектора-столбца х достаточно вычислить выражение A\b.
Деление
слева (\)
для квадратных матриц реализует метод Гаусса;
для прямоугольных матриц–
метод наименьших квадратов.Слайд 21Вместо знака обратной косой черты можно использовать функцию mldivide
x=mldivide(A,b)
Результат будет
тем же самым.
Слайд 22Функция solve() позволяет решить систему уравнений. Например, для системы уравнений
вида
>> [x y] = solve('2*x+y=3', '3*x-5*y=11', x, y)
x
= 2 y = -1




















![Аналитические вычисления в Matlab Функция solve() позволяет решить систему уравнений. Например, для системы уравнений вида Функция solve() позволяет решить систему уравнений. Например, для системы уравнений вида >> [x y] = solve('2*x+y=3', '3*x-5*y=11',](/img/thumbs/0d2e1be165c55f0fa69bd091d748242b-800x.jpg)































