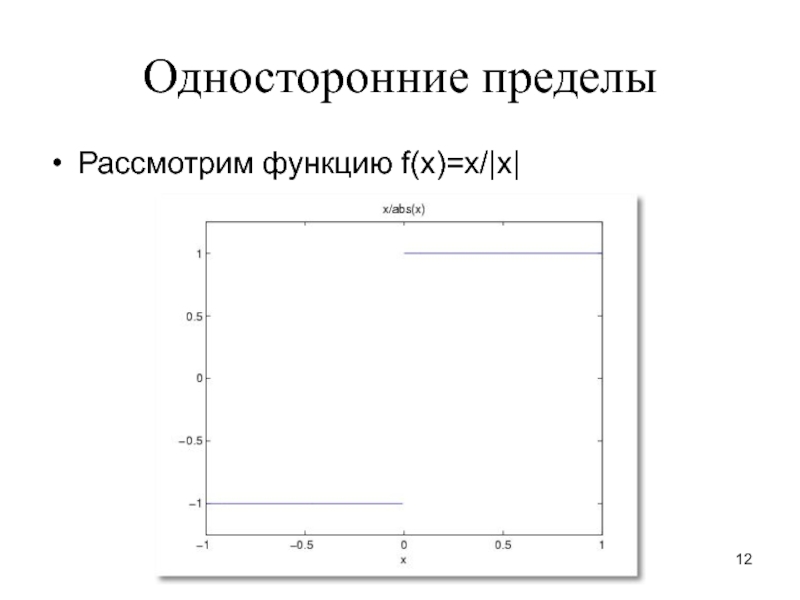
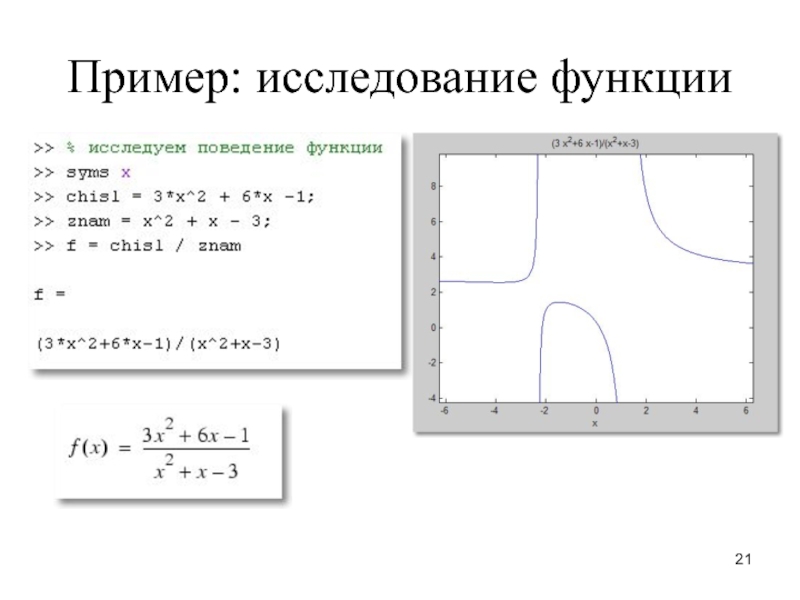
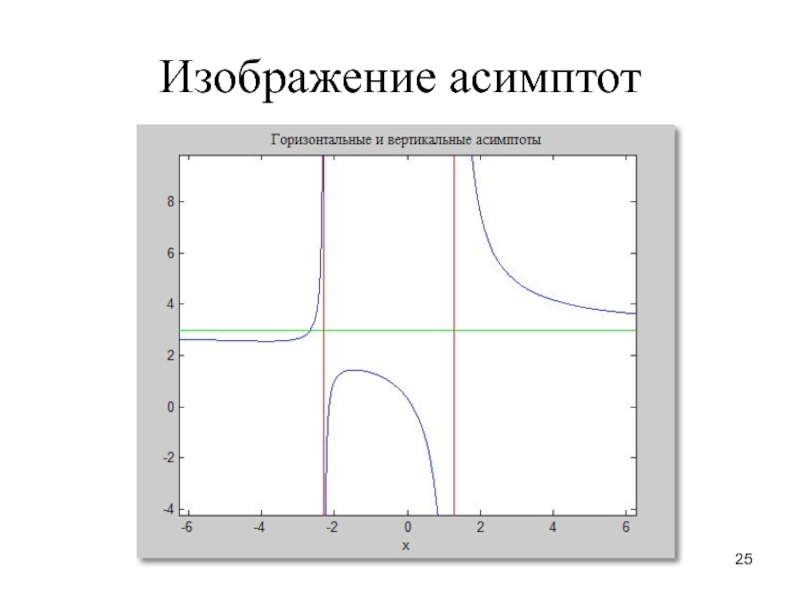
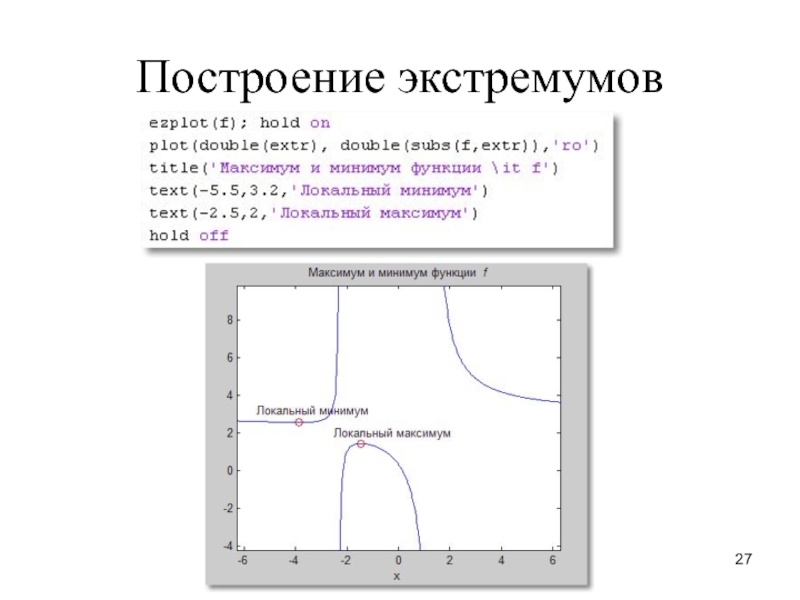
– F(a), где F(x) – первообразная
получаем точный результат
но первообразную
не всегда можно найти Численно: методом прямоугольников, трапеций, Симпсона и пр.
можно пользоваться даже тогда, когда интеграл «не берётся»
но при вычислении возникают погрешности