Слайд 1Анализ
информационных моделей
Презентация 11-18
Слайд 2Поиск определённого маршрута
по таблице
1. В таблицах приведена стоимость перевозки
грузов между соседними станциями. Если пересечение строки и столбца пусто,
то соответствующие станции не являются соседними. Укажите номер таблицы, для которой выполняется условие «Максимальная стоимость перевозки грузов от пункта В до пункта D не больше 6».
1 2 3 4
2
Слайд 3Поиск определённого маршрута
по таблице
2. В таблицах приведена стоимость перевозки
грузов между соседними станциями. Если пересечение строки и столбца пусто,
то соответствующие станции не являются соседними. Укажите номер таблицы, для которой выполняется условие «Минимальная стоимость перевозки грузов от пункта A до пункта D не больше 3».
1 2 3 4
3
Слайд 4Поиск оптимального маршрута
по расписанию
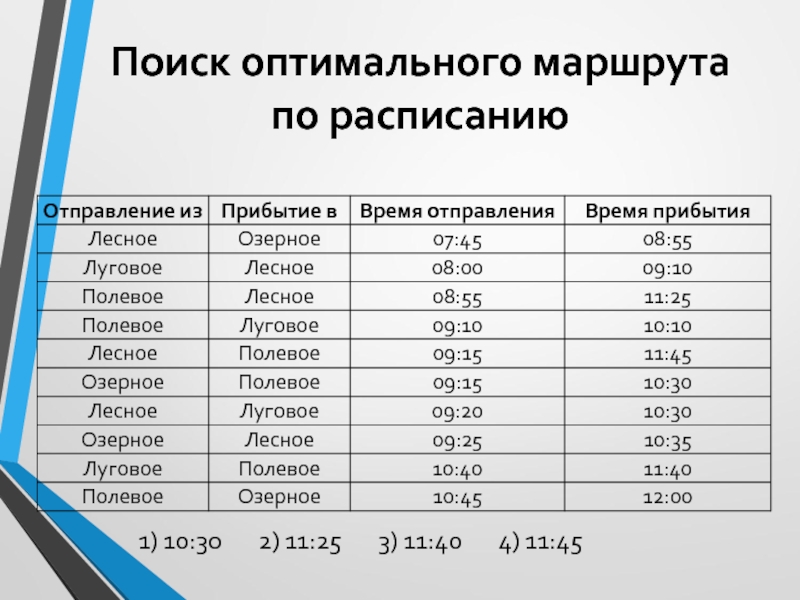
3. Путешественник пришел в 08:00 на
автостанцию поселка ЛЕСНОЕ и увидел расписание автобусов.
Определите самое раннее время,
когда путешественник сможет оказаться в пункте ПОЛЕВОЕ согласно этому расписанию.
Слайд 5Поиск оптимального маршрута
по расписанию
1) 10:30 2) 11:25 3) 11:40 4) 11:45
Слайд 6Поиск оптимального маршрута
по расписанию
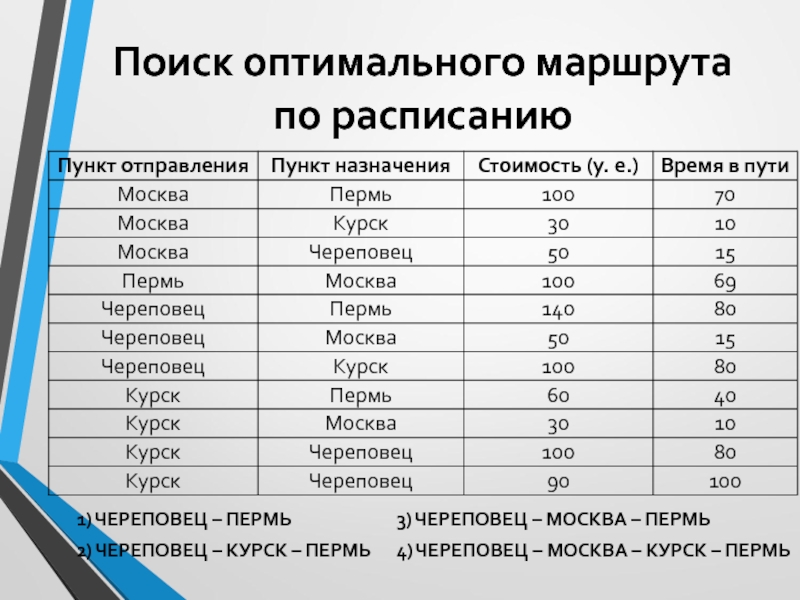
4. Транспортная фирма осуществляет грузоперевозки разными
видами транспорта между четырьмя городами: ЧЕРЕПОВЕЦ, МОСКВА, КУРСК, ПЕРМЬ. Стоимость
доставки грузов и время в пути указаны в таблице.
Определите маршрут наиболее дешевого варианта доставки груза из ЧЕРЕПОВЦА в ПЕРМЬ. Если таких маршрутов несколько, в ответе укажите наиболее выгодный по времени вариант.
Слайд 7Поиск оптимального маршрута
по расписанию
1) ЧЕРЕПОВЕЦ – ПЕРМЬ 3) ЧЕРЕПОВЕЦ –
МОСКВА – ПЕРМЬ
2) ЧЕРЕПОВЕЦ – КУРСК – ПЕРМЬ 4) ЧЕРЕПОВЕЦ –
МОСКВА – КУРСК – ПЕРМЬ
Слайд 8Поиск оптимального маршрута по таблице
5. Между населёнными пунктами A, B,
C, D, E, F построены дороги, протяжённость которых приведена в
таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)
Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
Слайд 9Таблицы и схемы
6. В таблице приведена стоимость
перевозки пассажиров между
соседними населенными пунктами.
Укажите схему, соответствующую
таблице.
1. 2. 3. 4.
Слайд 10Таблицы и схемы
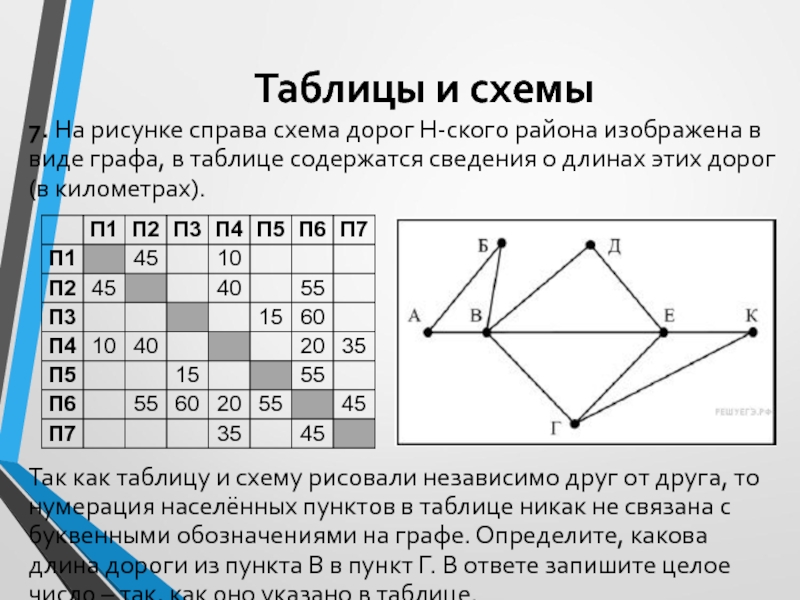
7. На рисунке справа схема дорог Н-ского района
изображена в виде графа, в таблице содержатся сведения о длинах
этих дорог (в километрах).
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта В в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.
Слайд 11Графы, содержащие менее десяти вершин
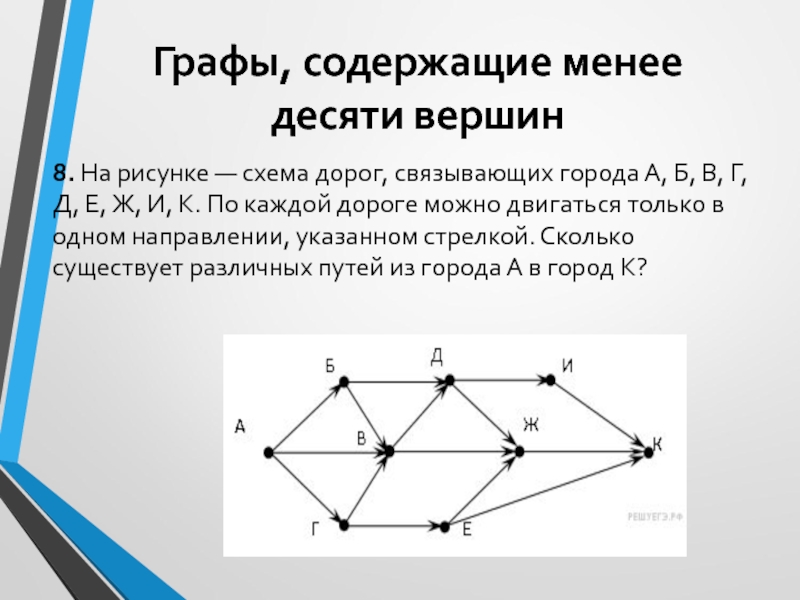
8. На рисунке — схема дорог,
связывающих города А, Б, В, Г, Д, Е, Ж, И,
К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Слайд 12Графы, содержащие менее десяти вершин
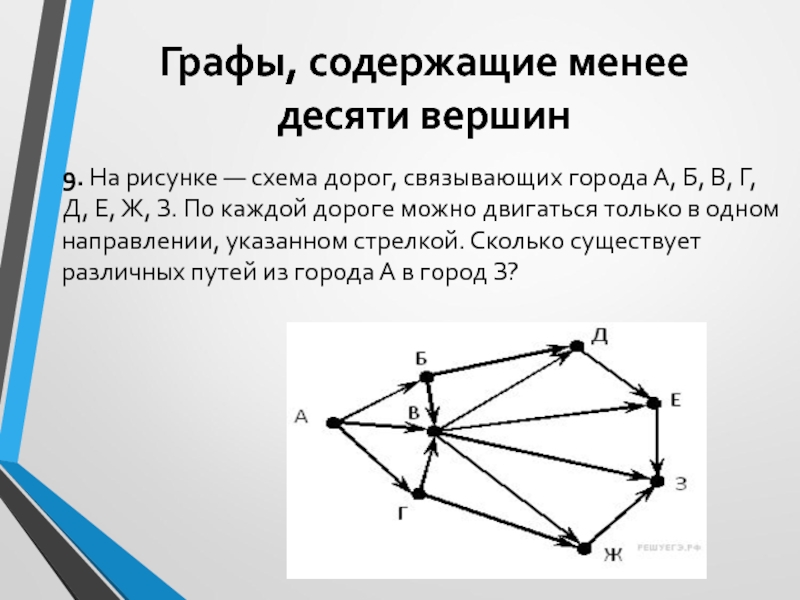
9. На рисунке — схема дорог,
связывающих города А, Б, В, Г, Д, Е, Ж, З.
По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?
Слайд 13Составление диаграммы
по данным
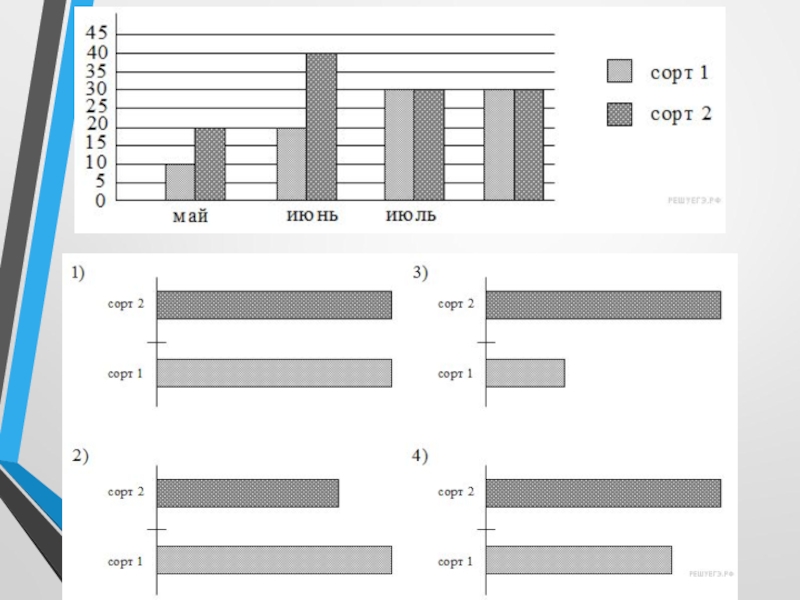
10. Диаграмма отражает количество (в килограммах) собранного
за четыре месяца урожая двух сортов огурцов в парниковом хозяйстве.
Какая
из диаграмм правильно отражает объемы суммарного за четыре месяца собранного урожая по каждому из сортов?
Слайд 15Составление диаграммы
по данным
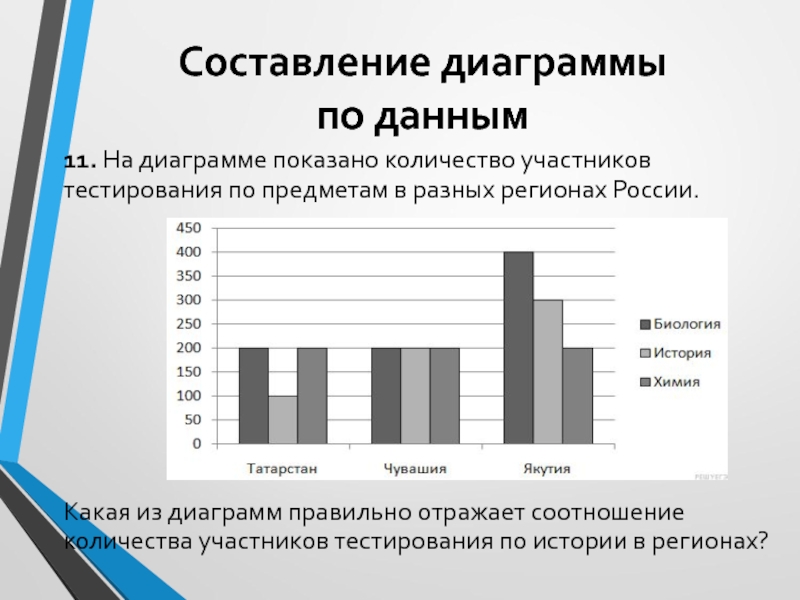
11. На диаграмме показано количество участников тестирования
по предметам в разных регионах России.
Какая из диаграмм правильно отражает
соотношение количества участников тестирования по истории в регионах?
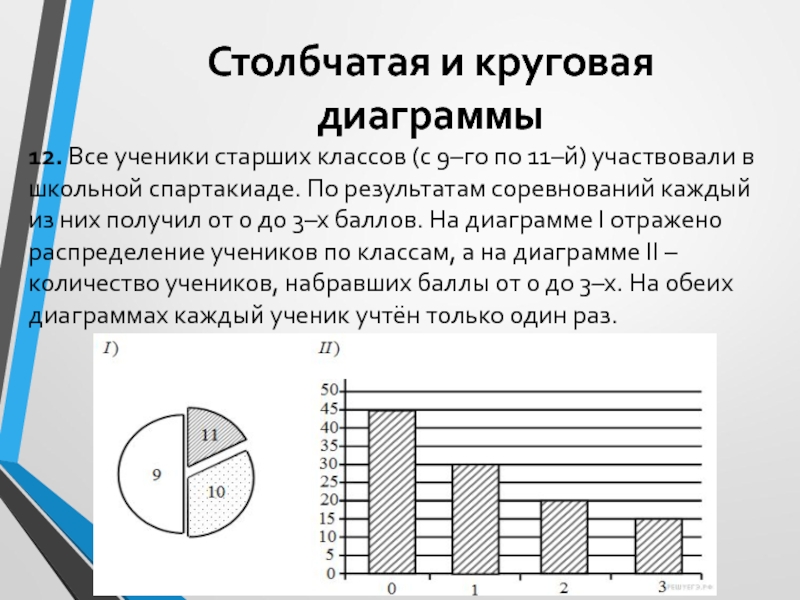
Слайд 17Столбчатая и круговая диаграммы
12. Все ученики старших классов (с 9–го
по 11–й) участвовали в школьной спартакиаде. По результатам соревнований каждый
из них получил от 0 до 3–х баллов. На диаграмме I отражено распределение учеников по классам, а на диаграмме II – количество учеников, набравших баллы от 0 до 3–х. На обеих диаграммах каждый ученик учтён только один раз.
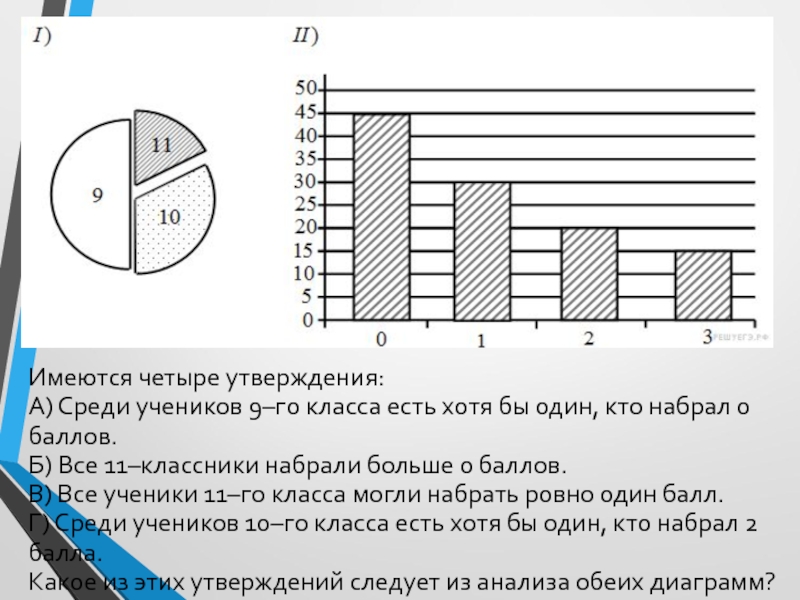
Слайд 18Имеются четыре утверждения:
А) Среди учеников 9–го класса есть хотя бы
один, кто набрал 0 баллов.
Б) Все 11–классники набрали больше 0
баллов.
В) Все ученики 11–го класса могли набрать ровно один балл.
Г) Среди учеников 10–го класса есть хотя бы один, кто набрал 2 балла.
Какое из этих утверждений следует из анализа обеих диаграмм?


















![АВТОМАТИЗАЦИЯ ЗВУКА [ Л ]
В СЛОВАХ](/img/tmb/6/598195/9904114927fd66f267234b3a5c44ea6c-800x.jpg)