Слайд 1Анализ цепей переменного тока
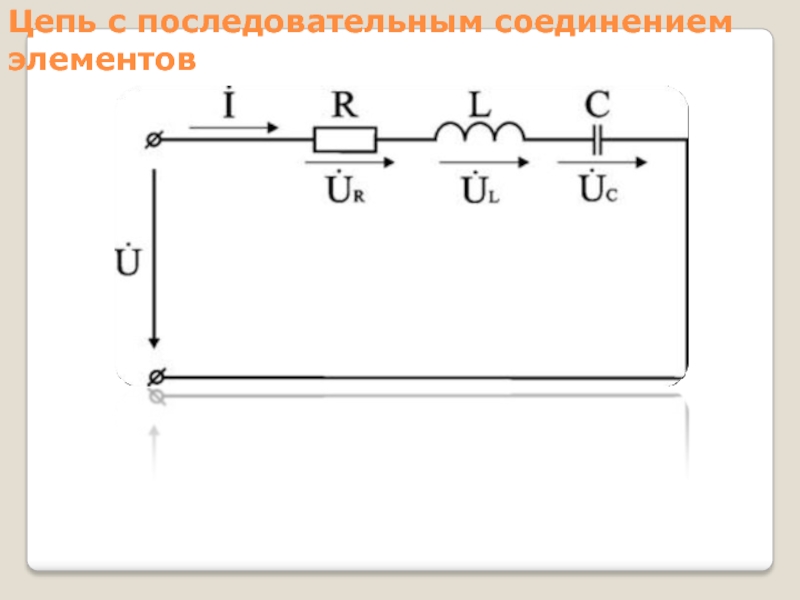
Слайд 2Цепь с последовательным соединением элементов
Слайд 3Построение векторной диаграммы
Слайд 4 Проведем анализ работы электрической цепи с последовательным соединением элементов: резистора
R, идеальной катушки с индуктивностью L и конденсатора с емкостью
С. Положим, что в этой задаче заданы величины R, L, С, частота f, напряжение U. Требуется определить ток в цепи и напряжение на элементах цепи.
Из свойства последовательного соединения следует, что ток во всех элементах цепи одинаковый.
Задача разбивается на ряд этапов.
1. Определение сопротивлений. Реактивные сопротивления идеальной катушки и конденсатора находим по формулам:
XL = ωL, XC = 1 / ωC, ω = 2πf.
Полное сопротивление цепи равно
угол сдвига фаз равен φ = arctg((XL - XC) / R)
Слайд 5 2. Нахождение тока.
Ток в цепи находится по закону Ома для
действующих значений тока и напряжения:
I = U / Z, ψi
= ψu + φ.
Фазы тока и напряжения отличаются на угол φ.
3. Расчет напряжений на элементах.
Напряжения на элементах определяются по формулам, составленным согласно закона Ома для действующих значений тока и напряжения, для каждого элемента цепи
UR = I R, ψuR = ψi ;
UL = I XL, ψuL = ψi + 90° ;
UC = I XC, ψuC = ψi - 90°.
Для напряжений выполняется второй закон Кирхгофа в векторной форме:
Слайд 64. Анализ расчетных данных.
В зависимости от величин L и
С в формуле расчета напряжений возможны следующие варианты:
XL > XC; XL
Для варианта XL > XC угол φ > 0, UL > UC. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид.
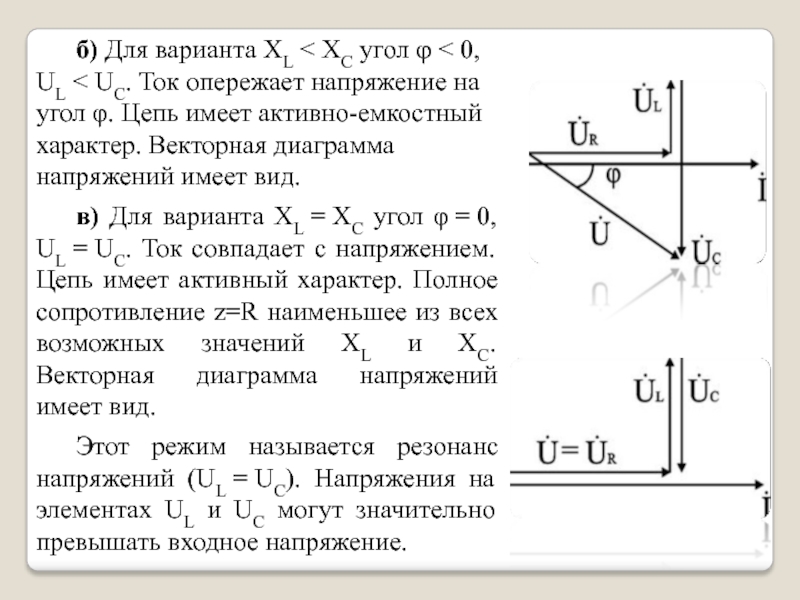
Слайд 7 б) Для варианта XL
на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет
вид.
в) Для варианта XL = XC угол φ = 0, UL = UC. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений XL и XC. Векторная диаграмма напряжений имеет вид.
Этот режим называется резонанс напряжений (UL = UC). Напряжения на элементах UL и UC могут значительно превышать входное напряжение.
Слайд 8Пример
Дано: U = 220 B, f = 50 Гц, R = 22 Ом, L = 350 мГн, С = 28,9 мкФ.
1. XL =
ωL = 2πf L = 2 · 3,14 · 50
· 0,35 = 110 Ом;
XC = 1 / ωC = 1 / (2πf C) = 110 Ом;
Z = R = 22 Ом, φ=0,
2. I = U / R = 220 / 22 = 10 А, ψu = ψi;
UL = UC = I XL = 10 · 110 = 1100 В.
В приведенном примере UL и UС превышают входное напряжение в 5 раз.
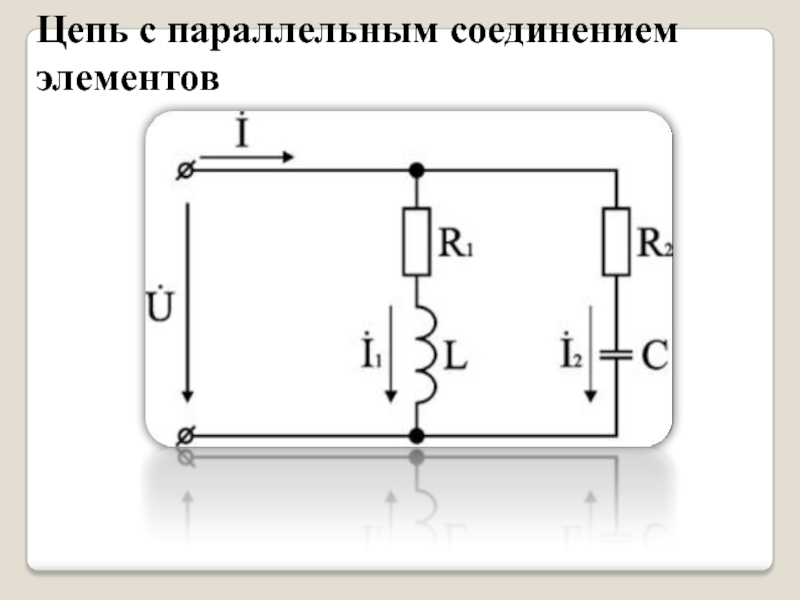
Слайд 9Цепь с параллельным соединением элементов
Слайд 10 Проведем анализ работы электрической цепи в состав которой входят параллельно
соединенные резистор, реальная катушка с внутренним сопротивлением и конденсатор.
Положим, что
заданы величины R1, R2, L, С, частота f и действующее значение входного напряжения U. Требуется определить токи в ветвях и ток всей цепи.
В данной схеме две ветви.
Согласно свойству параллельного соединения, напряжение на всех ветвях параллельной цепи одинаковое, если пренебречь сопротивлением подводящих проводов.
Задача разбивается на ряд этапов:
Слайд 11 1. Определение сопротивлений ветвей.
Реактивные сопротивления катушки и конденсатора определяем по
формулам
XL = ωL, XC = 1 / ωC, ω =
2πf.
Полное сопротивление ветвей равны
, ,
соответствующие им углы сдвига фаз
φ1 = arctg(XL /R1), φ2 = arctg(XС /R2).
2. Нахождение токов в ветвях.
Токи в каждой ветви находятся по закону Ома для действующих значений тока и напряжений:
I1 = U / Z1, ψi1 = ψu + φ1, I2 = U / Z2, ψi2 = ψu + φ2.
Слайд 12 3. Нахождение тока всей цепи.
Ток всей цепи может быть найден
несколькими методами: графическим, методом мощностей, методом проекций и методом проводимостей.
Чаще
всего используют метод проекций и метод проводимостей.
В методе проекций ток I1 и I2 раскладываются на две ортогональные составляющие - активную и реактивную. Ось активной составляющей совпадает с вектором напряжения U. Ось реактивной составляющей перпендикулярна вектору U.
Слайд 13 Активные составляющие токов равны
I1а = I1 cos φ1, I2а =
I2 cos φ2,
Iа = I1а + I2а.
Реактивные составляющие токов равны
I1р
= I1 sin φ1, I2р = I2 sin φ2,
Iр = I1р — I2р.
В последнем уравнении взят знак минус, поскольку составляющие I1р (индуктивная) и I2р (емкостная) направлены в разные стороны от оси U.
Полный ток находится
Угол сдвига фаз между током и напряжением во всей цепи
φ = arctg(Iр / Iа).
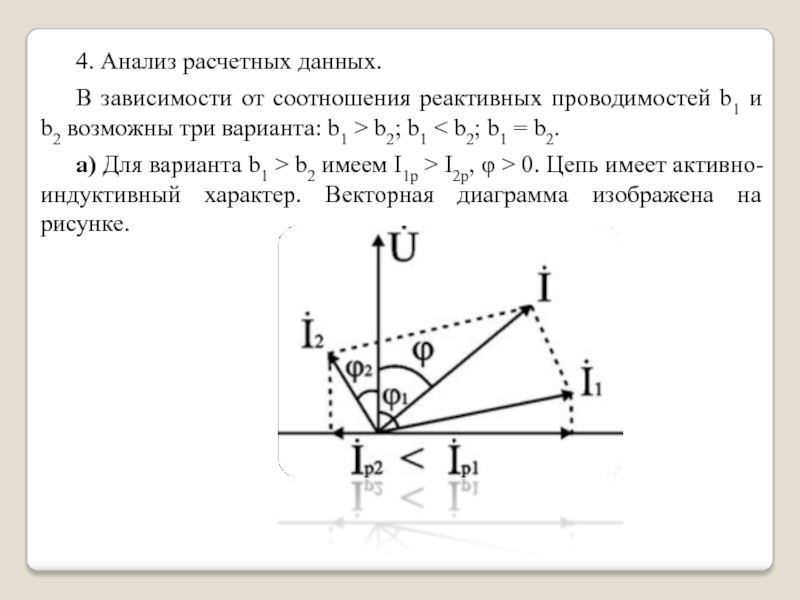
Слайд 14 4. Анализ расчетных данных.
В зависимости от соотношения реактивных проводимостей b1
и b2 возможны три варианта: b1 > b2; b1
b1 > b2 имеем I1р > I2р, φ > 0. Цепь имеет активно-индуктивный характер. Векторная диаграмма изображена на рисунке.
Если b1 = b2, то I1р = I2р, φ = 0. Цепь имеет чисто активное сопротивление.
Ток потребляемый цепью от источника наименьший. Этот режим называется резонанс токов.
Векторные диаграммы изображены на рисунках.
Слайд 16 Активная мощность потребителя определена формулой
P = U I cos φ.
Величину
cos φ здесь называют коэффициентом мощности. Ток в линии питающей потребителя
с заданной мощностью Р равен
I = P / (U cos φ),
и будет тем больше, чем меньше cos φ.
При этом возрастают потери в питающей линии. Для их снижения желательно увеличивать cos φ. Большинство потребителей имеет активно-индуктивную нагрузку. Увеличение cos φ возможно путем компенсации индуктивной составляющей тока путем подключения параллельно нагрузке конденсатора .
Повышение коэффициента мощности в электрической цепи
Слайд 17 Расчет емкости дополнительного конденсатора для обеспечения заданного cos φ проводится следующим
образом. Пусть известны параметры нагрузки Pн, U и Iн .
Можно определить cosφн
cos φн = P / (U Iн).
Подключение емкости не изменяет активную составляющую нагрузки
Iна = Iн cos φн = Pн / U.
Реактивная составляющая нагрузки Iнр может быть выражена через tg φн
Iнр = Iна tg φн.
При подключении емкости величина Iнр уменьшается на величину IC.
Если задано, что коэффициент мощности в питающей линии должен быть равен cos φ, то можно определить величину реактивной составляющей тока в линии
Iр = Iа tg φ.
Слайд 18 Уменьшение реактивной составляющей нагрузки с Iнр до Iр определяет величину
тока компенсирующей емкости
IC = Iнр - Iр = Iа (tg φн - tg φ).
Подставляя в
данное уравнение, значение Iна и учитывая, что IC = U / XC = U ωC, получим
U ωC = Pн / U · (tg φн - tg φ),
откуда для емкости конденсатора имеем
C = Pн / ωU2 · (tg φн - tg φ).
Для больших значений Pн величина емкости C может оказаться слишком большой, что технически трудно реализовать. В этом случае используют синхронные компенсирующие машины.
Слайд 19 Достоинство комплексного метода: при его применении в анализе цепей переменного
тока можно применять все известные методы анализа постоянного тока.
Закон Ома
Под
законом Ома в комплексной форме понимают:
Í = Ú / Z
Комплексное сопротивление участка цепи представляет собой комплексное число, вещественная часть которого соответствует величине активного сопротивления, а коэффициент при мнимой части – реактивному сопротивлению.
Законы Ома и Кирхгофа в комплексной форме
Слайд 20Примеры
По виду записи комплексного сопротивления можно судить о характере участка
цепи:
R + j X — активно-индуктивное сопротивление;
R – j X — активно-емкостное.
Слайд 21Первый закон Кирхгофа в комплексной форме
Алгебраическая сумма комплексных действующих значений
токов в узле равна нулю.
Второй закон Кирхгофа в комплексной форме
В
замкнутом контуре электрической цепи алгебраическая сумма комплексных действующих значений ЭДС равна алгебраической сумме комплексных падений напряжений в нём.
Слайд 22 При использовании символического метода можно пользоваться понятиями мощностей. Но в
комплексной форме можно записать только полную мощность:
где Ï — комплексно-сопряженный ток.
Полная
мощность в комплексной форме представляет собой комплексное число, вещественная часть которого соответствует активной мощности рассматриваемого участка, а коэффициент при мнимой части – реактивной мощности участка. Значение знака перед мнимой частью: “+” означает, что напряжение опережает ток, нагрузка – активно-индуктивная; “–” означает, что нагрузка - активно-емкостная.
S cos φ ± j S sin φ = P ± j Q