Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ANALIZA WSPÓŁZALEŻNOŚCI ZJAWISK
Содержание
- 1. ANALIZA WSPÓŁZALEŻNOŚCI ZJAWISK
- 2. Analiza współzależnościWspółczynnik korelacji liniowej PearsonaWspółczynnik korelacji rang SpearmanaAnaliza zależnościLiniowa funkcja regresjiBadanie niezależności dwóch cech jakościowych
- 3. ISTOTA KORELACJI I REGRESJIKORELACJA daje możliwość stwierdzenia,
- 4. Sir Francis Galton – 1822-1911, prekursor badań
- 5. Zależność przyczynowa – rodzaj zależności, w której
- 6. Zmienna niezależna – zmienna która wywołuje zmiany,
- 7. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 8. Przykład Dla sześciu studentów zmierzono czas pisania egzaminu
- 9. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 10. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 11. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 12. WSPÓŁCZYNNIK KORELACJI PEARSONA
- 13. Korelacja ujemna, średnia Korelacja niewyraźna, znikoma Korelacja ujemna, b.silna Korelacja dodatnia, b.silna
- 14. Współczynnik korelacji rang Spearmana służy do opisu
- 15. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 16. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
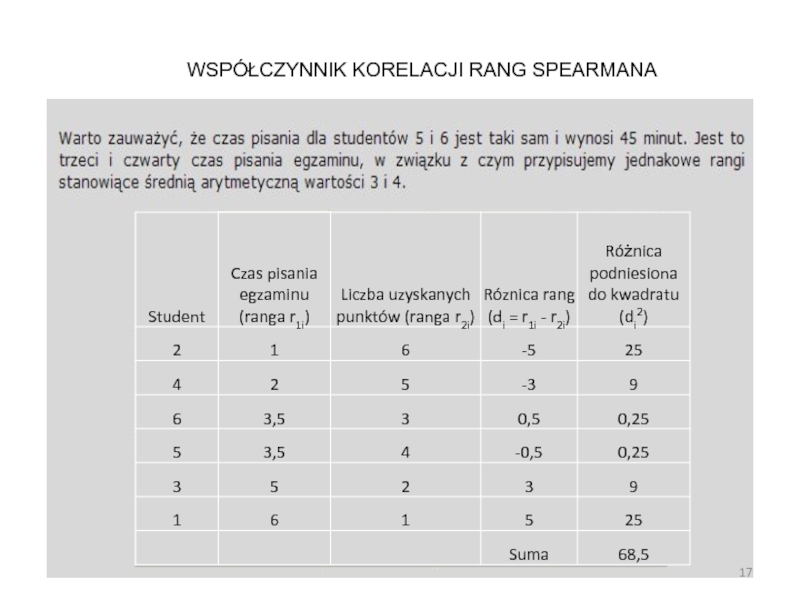
- 17. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 18. WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
- 19. W modelach regresji zależność pomiędzy jedną lub
- 20. Karol Fryderyk Gauss, ur. w 1777 roku
- 21. Funkcja regresji - to narzędzie do badania
- 22. FUNKCJA REGRESJI
- 23. FUNKCJA REGRESJI
- 24. Mamy do czynienia tylko z jedną zmienną
- 25. FUNKCJA REGRESJI
- 26. FUNKCJA REGRESJI
- 27. W wyjaśnianiu wielu zjawisk istotną rolę odgrywają
- 28. Dla danych jakościowych, mierzonych na skali nominalnej
- 29. W tym przypadku jako zmienną X przyjęliśmy
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Analiza współzależności
Współczynnik korelacji liniowej Pearsona
Współczynnik korelacji rang Spearmana
Analiza zależności
Liniowa funkcja
regresji
Слайд 3ISTOTA KORELACJI I REGRESJI
KORELACJA daje możliwość stwierdzenia, czy istnieje związek
(niekoniecznie przyczynowo-skutkowy) miedzy badanymi cechami (zmiennymi) oraz jaka jest jego
siła i kierunekREGRESJA daje możliwość oszacowania (estymacji) wartości jednej cechy (zmiennej zależnej, objaśnianej) na podstawie wartości przyjmowanych przez drugą cechę (zmienną niezależną, objaśniającą)
FUNKCJA REGRESJI, której parametry można oszacować przy pomocy metody najmniejszych kwadratów (MNK). Równanie opisujące związek statystyczny między zmiennymi nazywa się równaniem lub modelem regresji.
Слайд 4Sir Francis Galton – 1822-1911, prekursor badań nad inteligencją, statystyk,
meteorolog, antropolog, kryminolog. Pisarz, lekarz.
W 1899 r. w pracy
„Naturalna dziedziczność” ogłosił, że rozmiary nasion groszku pachnącego mają tendencję w kolejnych generacjach do powracania (to regress) do swego średniego rozmiaru, podobnego związku dopatrzył się także między wzrostem syna i ojca itd.Dopasowywał do tych par liczb linię prostą opisującą tę zależność
Слайд 5Zależność przyczynowa – rodzaj zależności, w której jesteśmy w stanie
wskazać, która ze zmiennych stanowi przyczynę zmian, a która ilustruje
skutek. Przykładem zależności przyczynowej może być związek pomiędzy stażem pracy (przyczyna) i wysokością zarobków (skutek).Zależność pozorna – pomiędzy dwoma zjawiskami wydaje się istnieć zależność, ale jest ona wywołana istnieniem wspólnej przyczyny. Przykładowo waga i poziom cholesterolu w organizmie wydają się być powiązane ze sobą, niemniej jednak jest to zależność pozorna. W rzeczywistości posiadają wspólną przyczynę – ilość i rodzaj spożywanych produktów
Zależność korelacyjna – zależność w której dla konkretnej wartości jednej zmiennej Xi (zmienna objaśniająca) odpowiada średnia arytmetyczna z kilku wartości drugiej zmiennej Y1, Y2, ...(zmienna objaśniania).
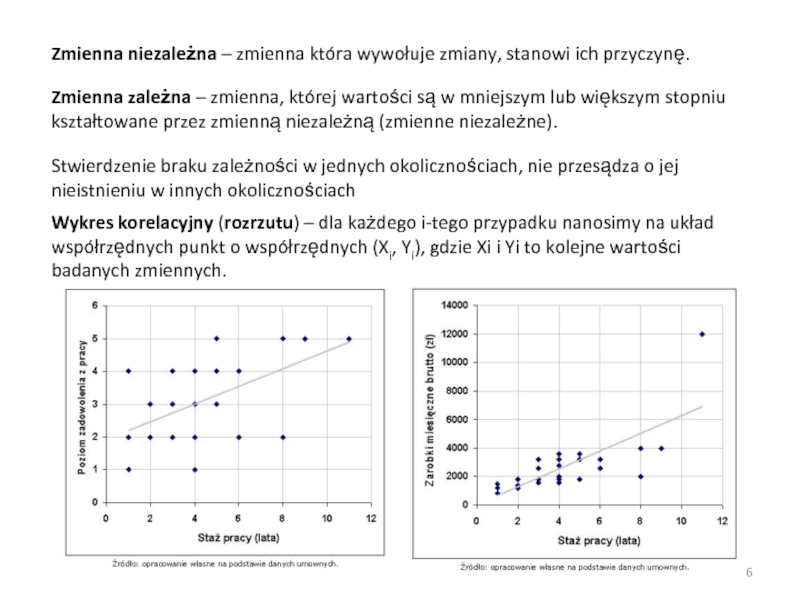
Слайд 6Zmienna niezależna – zmienna która wywołuje zmiany, stanowi ich przyczynę.
Zmienna
zależna – zmienna, której wartości są w mniejszym lub większym
stopniu kształtowane przez zmienną niezależną (zmienne niezależne).Stwierdzenie braku zależności w jednych okolicznościach, nie przesądza o jej nieistnieniu w innych okolicznościach
Wykres korelacyjny (rozrzutu) – dla każdego i-tego przypadku nanosimy na układ współrzędnych punkt o współrzędnych (Xi, Yi), gdzie Xi i Yi to kolejne wartości badanych zmiennych.
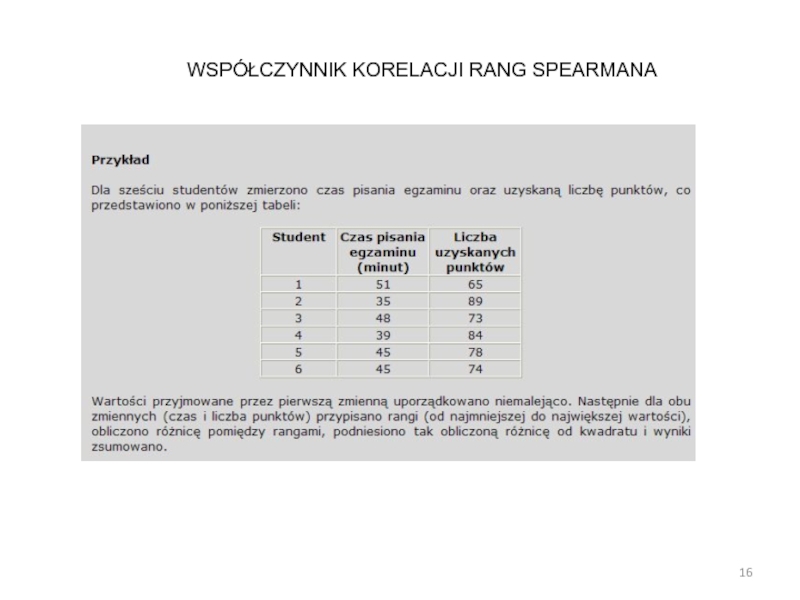
Слайд 8Przykład
Dla sześciu studentów zmierzono czas pisania egzaminu oraz uzyskaną liczbę
punktów. Obliczenia rozpoczynamy od ustalenia średnich dla zmiennej X (czas
pisania) oraz Y (liczba punktów):WSPÓŁCZYNNIK KORELACJI PEARSONA
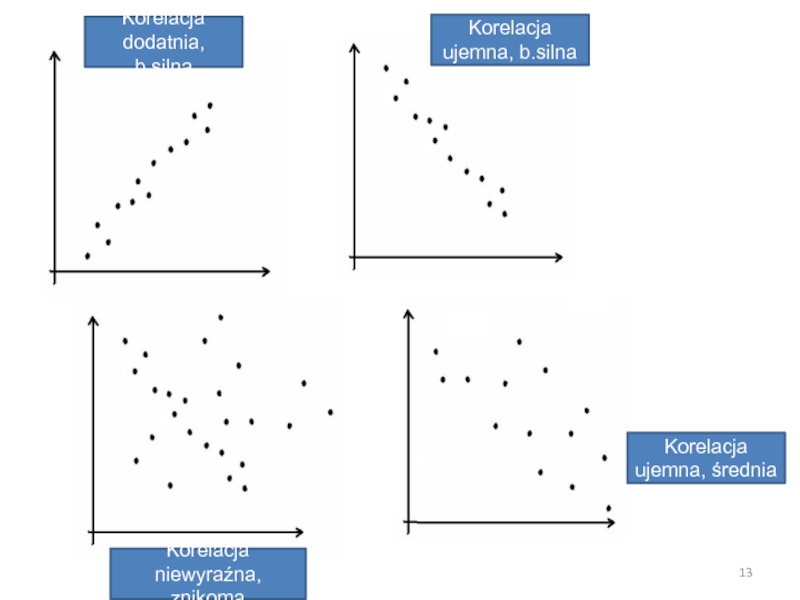
Слайд 13Korelacja ujemna, średnia
Korelacja niewyraźna, znikoma
Korelacja ujemna, b.silna
Korelacja
dodatnia, b.silna
Слайд 14Współczynnik korelacji rang Spearmana służy do opisu siły korelacji dwóch
cech w przypadku gdy:
Cechy są mierzalne, a badana zbiorowość jest
nieliczna.Cechy mają charakter jakościowy i istnieje możliwość ich uporządkowania.
Współczynnik korelacji rang Spearmana stosuje się do analizy współzależności obiektów pod względem cech X i Y.
Kolejne etapy wyznaczania współczynnika korelacji rang Spearmana są następujące:
Jednostki danej zbiorowości statystycznej, ze względu na wielkość odpowiadającej im pierwszej cechy, porządkuje się.
Tak uporządkowanym ze względem na pierwszą cechę jednostkom, przypisuje się kolejne numery począwszy od 1. Jeżeli kilka jednostek ma tę samą wielkość cechy, wtedy z odpowiadających im kolejnych rang oblicza się średnią arytmetyczną i przydziela wszystkim jednostkom, z których ta średnia została obliczona. Następna jednostka otrzymuje już najbliższą, niewykorzystaną dotąd rangę. Ostatni numer powinien równać się łącznej liczbie jednostek.
Następnie dla jednostek drugiej cechy w analogiczny sposób przypisuje się numery począwszy od 1 (dla jednostki o najniższej lub najwyższej wartości).
WSPÓŁCZYNNIK KORELACJI RANG SPEARMANA
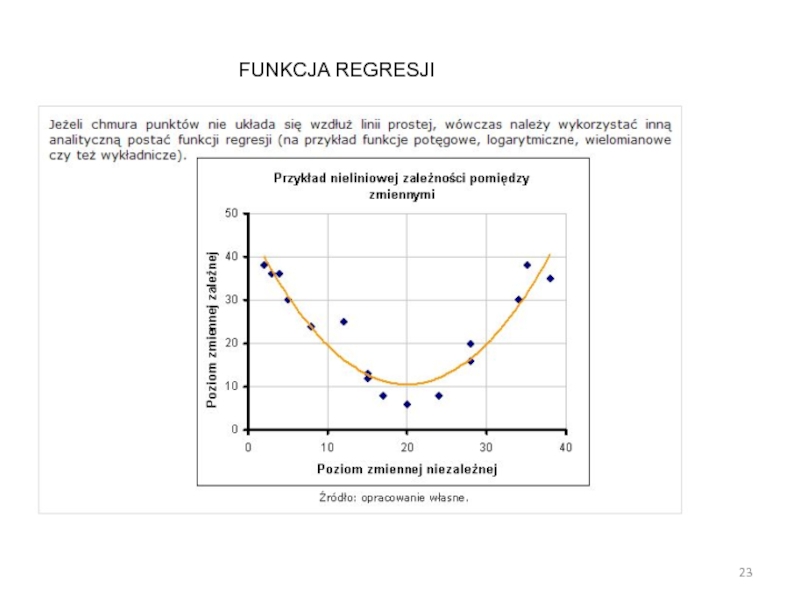
Слайд 19W modelach regresji zależność pomiędzy jedną lub większą ilością zmiennych
niezależnych (predykatory, zmienne wyjaśniające) a zmienną zależną (zmienna wyjaśniana) przedstawiamy
w postaci tak zwanej funkcji regresji.Poniżej przedstawiono przykłady wykorzystania modeli regresji do rozwiązywania praktycznych problemów:
Określenie zależności pomiędzy wiekiem, poziomem wykształcenia (mierzonym na przykład przez liczbę lat), stażem pracy a wysokością zarobków w danej branży.
Określeniem wpływu działań marketingowych (mierzonych na przykład wydatkami na reklamy telewizyjne, prasowe, billboardy, etc.) na przyszłą sprzedaż produktu.
Określenie wpływu wieku, wagi, aktywności ruchowej (mierzonej na przykład liczbą godzin w tygodniu przeznaczoną na uprawianie sportu) a kondycją fizyczną (mierzoną na przykład wynikiem biegu na 1km).
FUNKCJA REGRESJI
Слайд 20Karol Fryderyk Gauss, ur. w 1777 roku w Niemczech. Ojciec
Karola był pomocnikiem murarskim i swojego syna początkowo przeznaczał do
podobnej kariery. Na szczęście niepospolity talent młodziutkiego Gaussa objawił się na tyle wcześnie i w sposób tak ewidentny, że znalazł się oświecony i możny sponsor, dzięki któremu matematyka nie straciła jednego ze swoich najwybitniejszych uczonych. Nauczycielu matematyki kazał swoim uczniom (8-9letnim) obliczyć sumę liczb od 1 do 100. Karol po pięciu minutach przedstawił kartkę z rzeczywiście króciutkim wywodem:101x50=5050
Jeszcze jako uczeń gimnazjum Gauss sformułował metodę najmniejszych kwadratów
Слайд 21Funkcja regresji - to narzędzie do badania powiązań między zmiennymi.
Funkcja regresji to analityczny wyraz przyporządkowania średnich wartości zmiennej zależnej
konkretnym wartością zmiennej niezależnej.Dużym problemem jest wybór postaci analitycznej funkcji dla danego problemu. Ułatwieniem może być sporządzenie m.in. wykresu rozrzutu, gdzie dla każdej (i-tej) pary wartości zmiennej niezależnej (X) i zmiennej zależnej (Y) tworzymy punkt o współrzędnych Xi, Yi.
Jeżeli zmiennych niezależnych jest więcej, wówczas konstruujemy odpowiednio większą ilość wykresów rozrzutu, przedstawiających zależność pomiędzy każdą zmienną niezależną (oś pozioma) a zmienną niezależną. Z wykresu (wykresów) odczytujemy prawdopodobny rodzaj zależności pomiędzy zmiennymi niezależnymi a zmienną zależną.
FUNKCJA REGRESJI
Слайд 24
Mamy do czynienia tylko z jedną zmienną niezależną X.
Zależność
pomiędzy zmienną niezależną X a zmienną zależną Y ma charakter
liniowy.Naszym zadaniem jest wyznaczenie liniowej funkcji regresji, o ogólnej postaci:
y = a + bx
Gdzie:
y - wartość przewidywana na podstawie wartości x
a - parametr a jest nazywany wyrazem wolnym i odpowiada wartości funkcji y dla argumentu x = 0
b - współczynnik kierunkowy, który decyduje o tym, czy funkcja jest rosnąca, czy malejąca oraz jak szybko następują zmiany (jeśli b jest dodatnie, to funkcja jest rosnąca – to znaczy, im większe wartości zmiennej x, tym większe wartości funkcji, czyli y)
Do wyznaczenia parametrów tej funkcji (a i b) wykorzystuje się metodę najmniejszych kwadratów.
FUNKCJA REGRESJI
Слайд 27W wyjaśnianiu wielu zjawisk istotną rolę odgrywają zmienne niemierzalne, tj.
jakościowe.
I tak, na wielkość popytu na dany produkt oprócz jego
walorów użytkowych wielki wpływ ma marka. Dotyczy to w szczególności takich produktów jak samochody, odzież, zegarki czy sprzęt elektroniczny. W analizie wydajności pracy w rozmaitych zawodach istotną rolę odgrywa płeć pracownika. Ma ona także wpływ na wynagrodzenie.To ostanie z kolei w sposób oczywisty zależy od stanowiska. Wielkość dochodów ludności zależy od kraju, który ona zamieszkuje, itd.
Podobne wielkości występują przy analizie rozmaitych procesów chemicznych czy fizycznych (np. rodzaj użytego tworzywa, sposób (technika) obróbki, itp.)
Wartości zmiennej jakościowej nazywamy kategoriami lub wariantami.
Jeśli różnych kategorii zmiennej jakościowej jest stosunkowo niewiele, to zmienną taką możemy łatwo włączyć do modelu regresji.
Слайд 28Dla danych jakościowych, mierzonych na skali nominalnej lub porządkowej analizę
współzależności zwykle rozpoczynamy od utworzenia tabeli krzyżowej. W pierwszej kolumnie
warianty cechy X, natomiast w pierwszym wierszu tabeli umieszczamy warianty zmiennej Y. Możliwe jest także utworzenie tabeli krzyżowej dla zmiennych ilościowych, mierzonych na skali przedziałowej lub ilorazowej. Wówczas gdy liczba wszystkich przyjmowanych wartości przez zmienną X i Y (liczbę możliwych wartości będziemy oznaczać symbolami k i l) jest względnie mała, wpisujemy je wszystkie w odpowiednie wiersze i kolumny. W przypadku dużej liczby możliwych wartości niezbędne jest ich pogrupowanie przy użyciu przedziałów klasowych.WSPÓŁZALEŻNOŚC CECH JAKOŚCIOWYCH
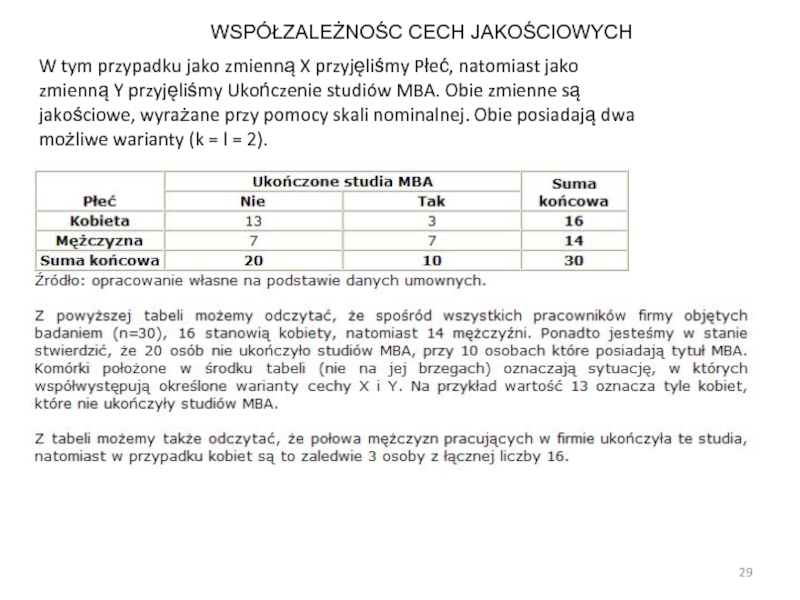
Слайд 29W tym przypadku jako zmienną X przyjęliśmy Płeć, natomiast jako
zmienną Y przyjęliśmy Ukończenie studiów MBA. Obie zmienne są jakościowe,
wyrażane przy pomocy skali nominalnej. Obie posiadają dwa możliwe warianty (k = l = 2).WSPÓŁZALEŻNOŚC CECH JAKOŚCIOWYCH