Геометрические построения. Линии сопряжения. Сопряжение линий

на экран не выводится. Его можно удалить
Здесь находится небольшая аннотация,

а также заготовка для возможного расширения презентации – для создания других построений в будущем. В принципе, этот слайд можно удалить.
Презентация создана в помощь учителю при проведении уроков технологии или черчения. Все рассмотренные случаи расположены в порядке возрастания сложности.

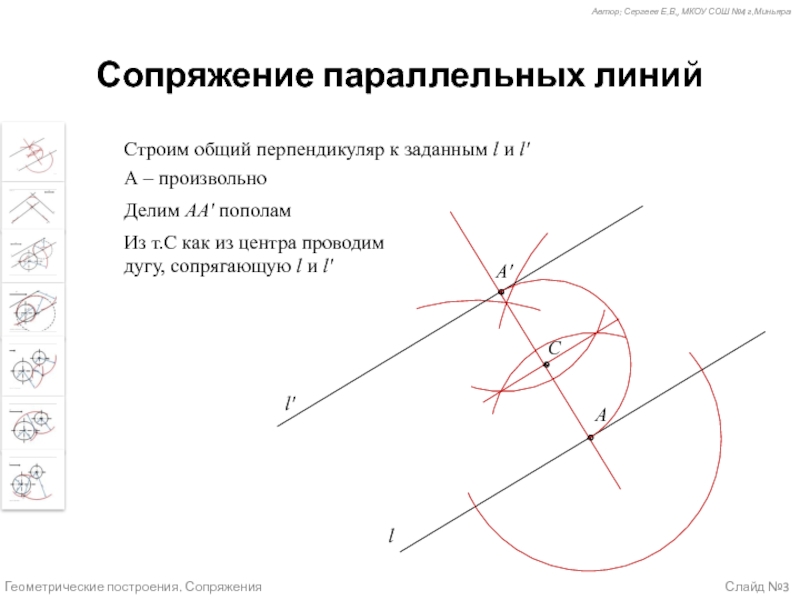
Случай 1 (слайд №3) – Сопряжение параллельных линий
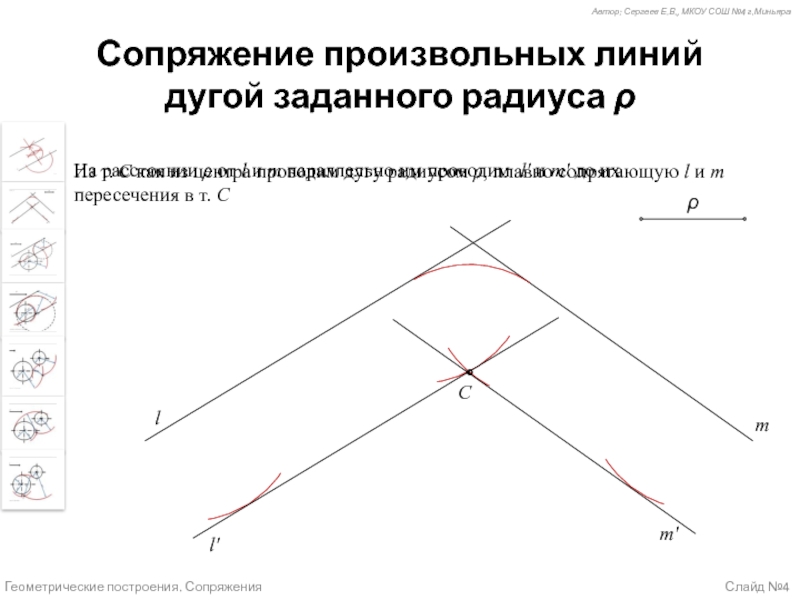
Случай 2 (слайд №4) – Сопряжение произвольных линий дугой заданного радиуса
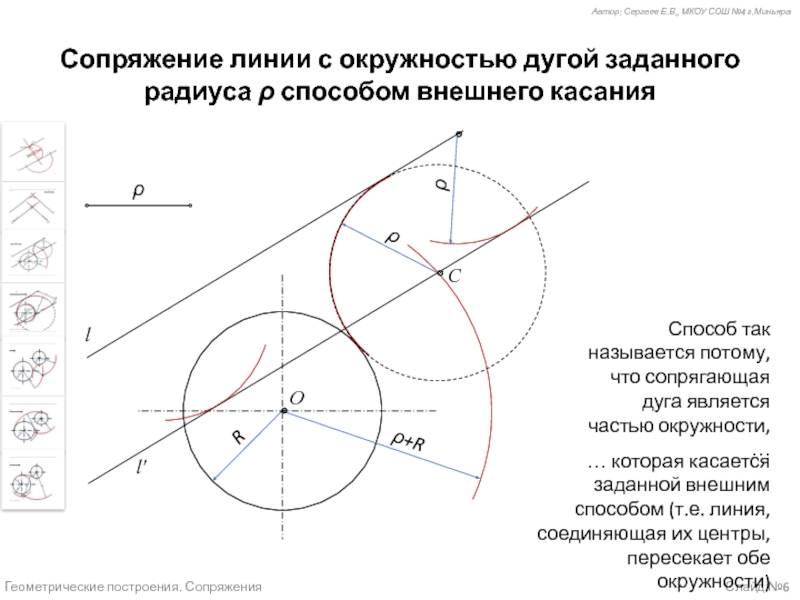
Случай 3 (слайд №6) – Сопряжение линии с окружностью дугой заданного радиуса способом внешнего касания
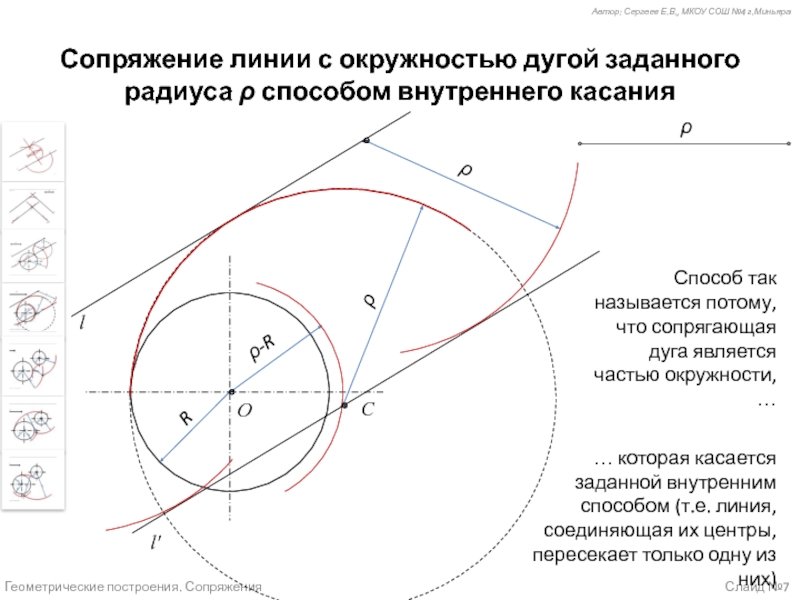
Случай 4 (слайд №7) – Сопряжение линии с окружностью дугой заданного радиуса способом внутреннего касания
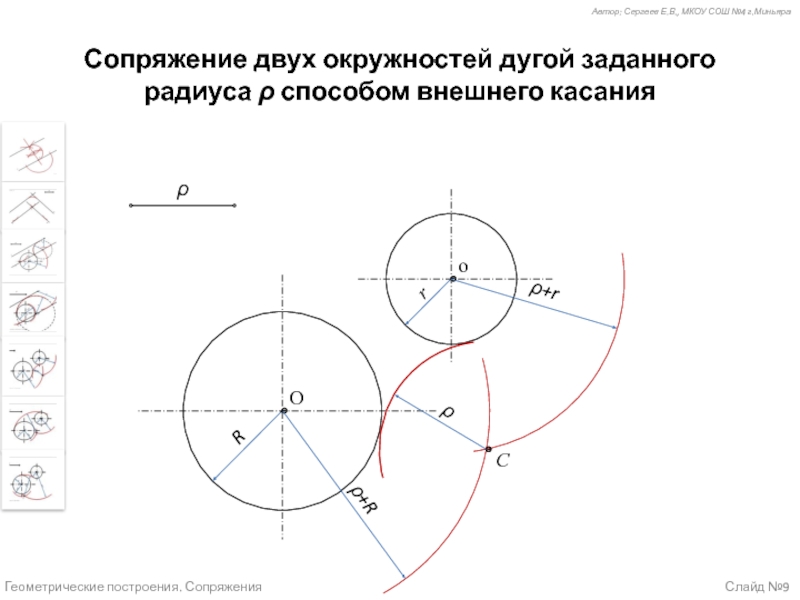
Случай 5 (слайд №9) – Сопряжение двух окружностей дугой заданного радиуса способом внешнего касания
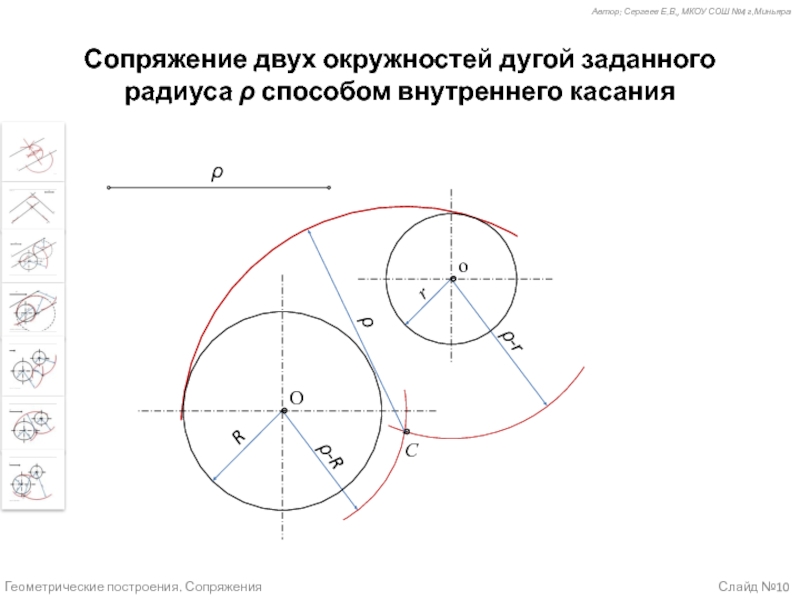
Случай 6 (слайд №10) – Сопряжение двух окружностей дугой заданного радиуса способом внутреннего касания
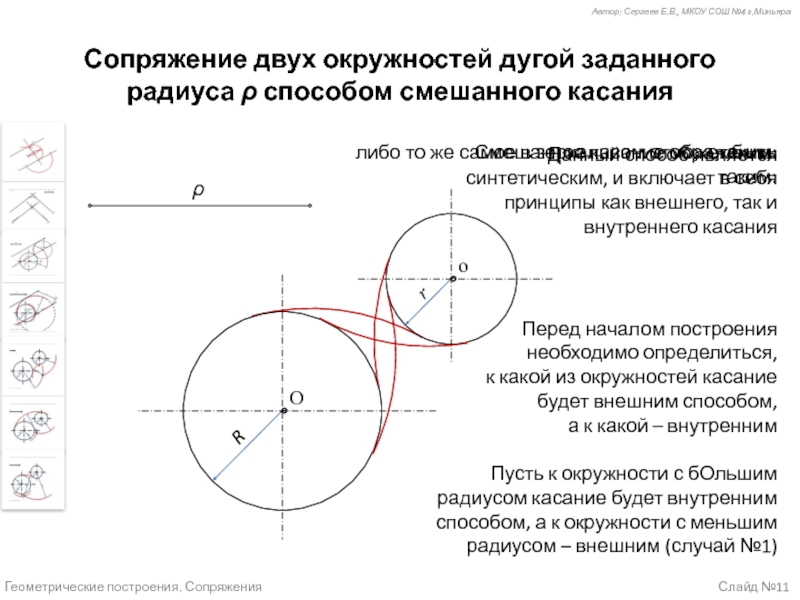
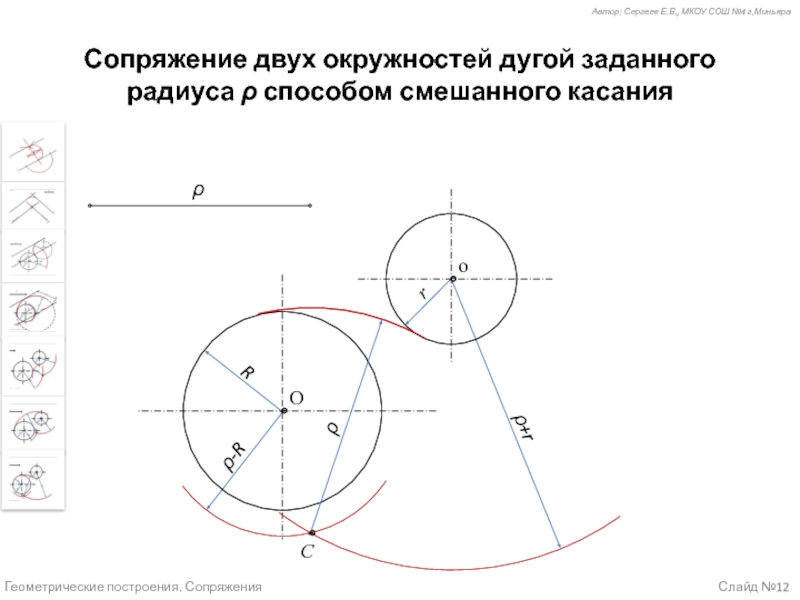
Случай 7 (слайд №11) – Сопряжение двух окружностей дугой заданного радиуса способом смешанного касания
Случай 8 (слайд №13) – Сопряжение двух окружностей способом перекрёстного касания

Презентация снабжена сквозной системой навигации по слайдам в виде иконок с изображением эскиза слайдов.

Об авторе
Сергеев Евгений Викторович, учитель технологии и учитель информатики МКОУ СОШ №4 г.Миньяра Челябинской области. E-mail: sergeev@uchportal.ru

Ограничения на использование презентации
Вы можете без каких-либо ограничений: - демонстрировать презентацию целиком или отдельными слайдами - добавлять на слайды свои текстовые метки
- копировать слайды для их использования в других презентациях
Вам НЕ разрешено:
- удалять мой копирайт в правом верхнем углу слайдов
- публиковать презентацию где-либо без согласования со мной

и l'
А'
Делим АА' пополам
C
Из т.С как из центра проводим дугу, сопрягающую

l и l'

и m параллельно им проводим l' и m' до их

пересечения в т. С

Из т. С как из центра проводим дугу радиусом ρ, плавно сопрягающую l и m

касания
l
ρ
ρ
О
С
l'
ρ
ρ+R
R
Способ так называется потому, что сопрягающая дуга является частью

окружности, …

… которая касается заданной внешним способом (т.е. линия, соединяющая их центры, пересекает обе окружности)

касания
l
ρ
ρ
О
l'
ρ
ρ-R
R
Способ так называется потому, что сопрягающая дуга является частью

окружности, …

… которая касается заданной внутренним способом (т.е. линия, соединяющая их центры, пересекает только одну из них)

С

ρ
C
ρ+r
ρ+R
ρ

ρ
ρ-R
C
ρ-r
ρ

ρ
Смешанное касание может быть таким:
таким:
либо то же самое в зеркальном

отображении:

Данный способ является синтетическим, и включает в себя принципы как внешнего, так и внутреннего касания

Перед началом построения необходимо определиться, к какой из окружностей касание будет внешним способом, а к какой – внутренним

Пусть к окружности с бОльшим радиусом касание будет внутренним способом, а к окружности с меньшим радиусом – внешним (случай №1)

ρ
ρ-R
ρ+r
С
ρ

касание двумя дугами разной кривизны)
1
х
2
1. Соединяем центры о и О оО

пересекает окружности в точках 1 и 2
2. Делим оО пропорционально радиусам:
из т. о радиусом о2 проводим дугу
из т. О радиусом О1 проводим дугу
точка х делит отрезок 12 пропорционально радиусам r и R. Она же является точкой перегиба линии сопряжения
3. Из центра о радиусом х1 проводим дугу
Из центра О радиусом х2 проводим дугу
4. Из точки х радиусом хо проводим дугу
Из точки х радиусом хО проводим дугу
5. Из точки С1 радиусом С1х проводим первую половину сопрягающей линии
6. Из точки С2 радиусом С2х проводим вторую половину сопрягающей линии

3

4

С1

С2

Внимание! Данный слайд скрыт из демонстрации. Дело в том, что такого способа сопряжения двух окружностей я так и не смог найти в справочниках, и мне пришлось разрабатывать его самому. Это может показаться нескромным, но, согласитесь, способ существует, и он весьма интересен. Кстати, его название также пришлось придумывать мне самостоятельно. Не возражаю, если Вы назовёте его как-то иначе

Если Вы, несмотря на все мои предупреждения, всё же готовы использовать этот слайд на своём уроке, то просто удалите этот баннер и снимите галочку «Скрыть слайд» в контекстном меню (правая кнопка мыши), вызванном на иконке слайда в слайдере (список слайдов в виде миниатюр слева от слайда).