Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Атомы
Содержание
- 1. Атомы
- 2. Физический атомЭнергияААС (атомная абсорбционная спектроскопия) АЭС (атомная эмиссионная спектроскопия) РФЭС (рентгеновская фотоэлектронная спектроскопия)
- 3. Механические моменты отличаются друг от друга не по энергии, а по другим характеристикам — механическим моментам
- 4. ( g — фактор Ланде )Полный (J), орбитальный (L) и спиновой (S) моменты
- 5. Орбитальный механический моментПолный механический моментСпиновой механический моментJ,
- 6. Квантовые числа
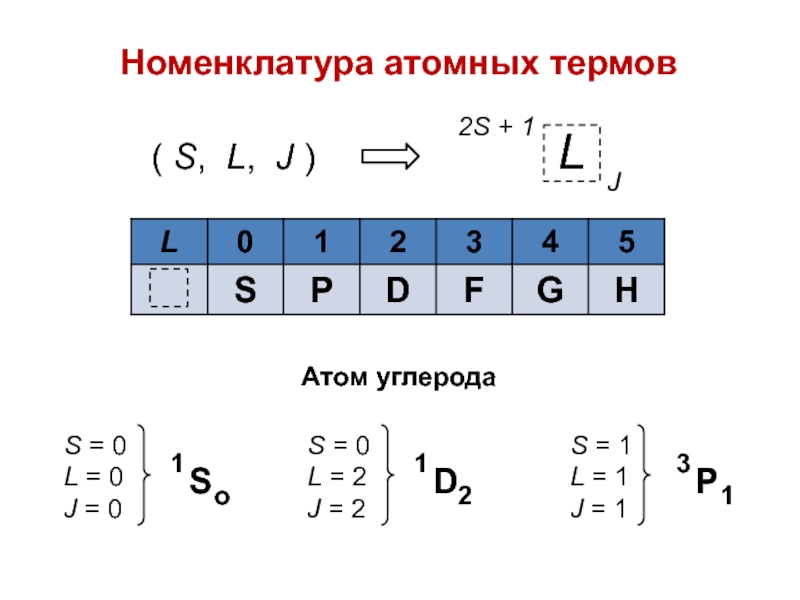
- 7. Номенклатура атомных термов( S, L, J ) Атом углерода
- 8. Глобальная волновая функцияH Φ = E ⋅
- 9. Локальная модель атомаС ГЛОБАЛЬНОЙ точки зрения любой
- 10. Одноэлектронное приближение (ОЭП)Свойства структуры — функция свойств частиц и взаимодействий
- 11. Одноэлектронное приближениеКаждому электрону приписывается:индивидуальная функция — «атомная
- 12. Проблема определения орбиталей и одночастичных наблюдаемых φi
- 13. ε1 = constε2 = constE = ε1 + ε2 = const
- 14. ε1 ≠ constε2 ≠ constE = ε1 + ε2 + Δ ε12 = const
- 15. Реальные электроныГлобальная энергия атомаЕ = Σ εi
- 16. Квази-электроны (орбитальная модель)Е = Σ ( εi )* + ΔΕ = const( εi )* = const
- 17. Нет способа вычислить теоретически или найти экспериментальными средствамиМожно найти методом подбора (вариационный принцип Ритца)
- 18. Электроны сами выбирают наиболее простые и экономные
- 19. Решение первой задачи Н Ф = EФ = E Ф = ?
- 20. Оператор ГамильтонаH = T + Uэя +
- 21. Пример: атом С (6 электронов)H = t1
- 22. hi = [(–2/2m)∇2i – Ze2/RiN ] —
- 23. Уравнения Хартри-Фока (ХФ-уравнения)δЕ = 0Fi = (hi
- 24. Система уравнений Хартри-Фока требует особого подхода. Ее
- 25. (φ1, φ2, ... ,
- 26. АО являются собственными функциями оператора Фока
- 27. Принципиальное различие: оператор потенциальной энергии в уравнении
- 28. Зависимость Uэфф от углов θ и ϕ
- 29. (φ*)ПЦП = f (r, θ, ϕ) = R'(r) ⋅ Θ(θ) ⋅ Φ(ϕ)
- 30. В многоэлектронном атоме сила притяжения электрона к
- 31. n — главное квантовое число, нумерующее радиальную
- 32. Эффективный заряд ядра Z* = Z –
- 33. Орбитали Слэтера-Зенера или "DZ-АО" (дубль-зет) — линейные
- 34. εi* = Hi + ∑ Jij
- 35. Слайд 35
- 36. Полная энергия МЭА
- 37. Оболочечная модель МЭА1. Одноэлектронное приближение: каждому электрону
- 38. Каждому электрону соответствует стандартный набор наблюдаемых, выражаемых
- 39. Слайд 39
- 40. Электронная конфигурация — способ распределения электронов по
- 41. Основная проблема оболочечной модели — нахождение устойчивых
- 42. Е1s2s3s4s2p3p4p3d4d
- 43. Число электронов в заполненной подоболочке называется ее
- 44. Слайд 44
- 45. Э. Резерфорд, 1934 г. «Развитие волновой механики
- 46. Одноэлектронное (орбитальное) приближениеНерелятивистское приближениеПриближение центрального поля
- 47. Заселение незаполненных оболочек Внутри каждой (n, )-оболочки
- 48. Поскольку орбитальные энергии всех 2р-АО одинаковы, на
- 49. 1. LS-приближение, справедливое для легких атомов (Z
- 50. При сложении векторов складываются их проекции. Атом
- 51. Длина проекции глобального вектора определяется суммой магнитных
- 52. MSML
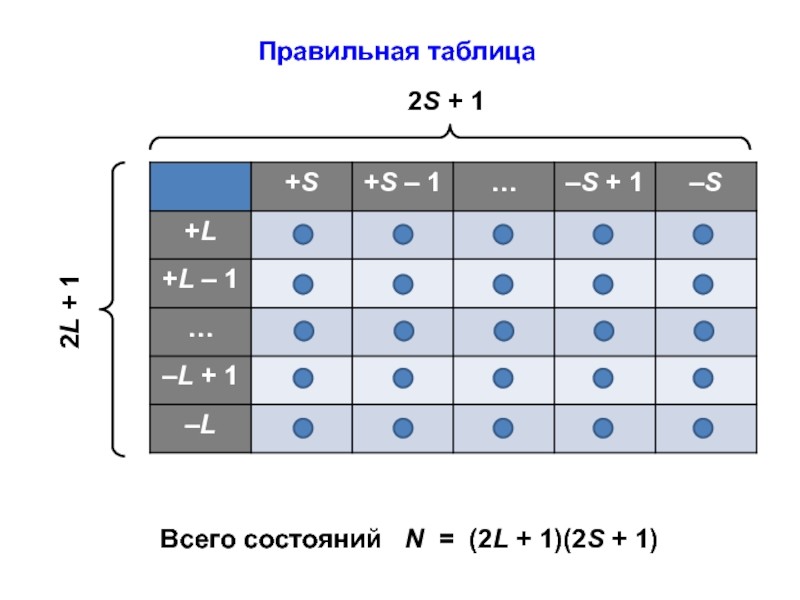
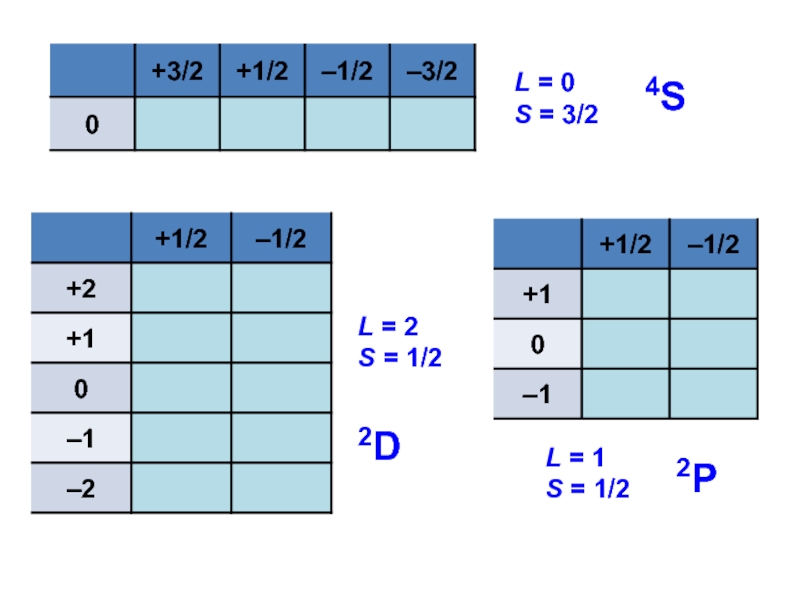
- 53. Правильная таблицаВсего состояний N = (2L + 1)(2S + 1)
- 54. MSML
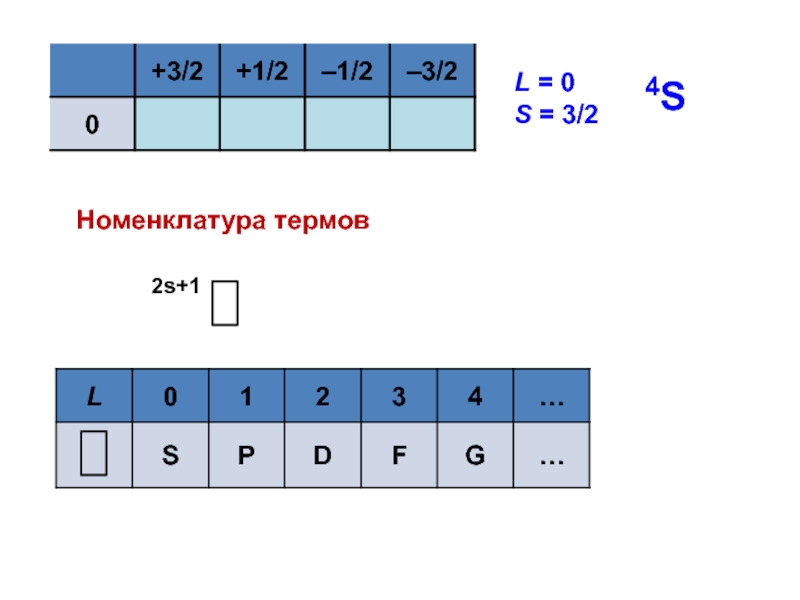
- 55. L = 0 S = 3/24SНоменклатура термов
- 56. MSML
- 57. L = 0 S = 3/2L = 2 S = 1/24S2D
- 58. MSML
- 59. L = 0 S = 3/2L
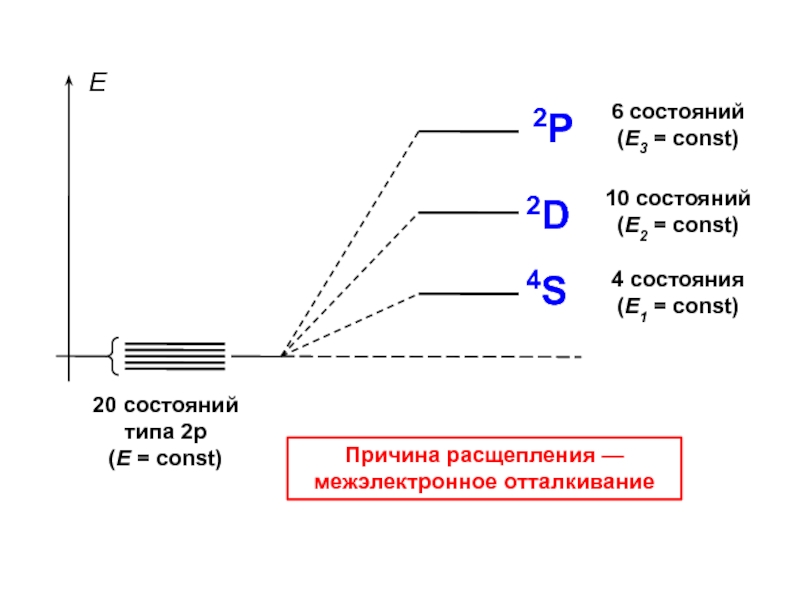
- 60. Зная принадлежность состояний к определенным термам, можно
- 61. Причина расщепления — межэлектронное отталкивание
- 62. Спин-орбитальное взаимодействиеПолная энергия атома зависит от взаимной
- 63. Вычисление величины полного момента| J |2 =
- 64. 3 правило Хунда:а) если подоболочка заполнена наполовину
- 65. Влияние внешнего магнитного поляВариант «слабого поля»
- 66. «Слабое поле»Внутренняя связь (спин-орбитальное взаимодействие) между векторами
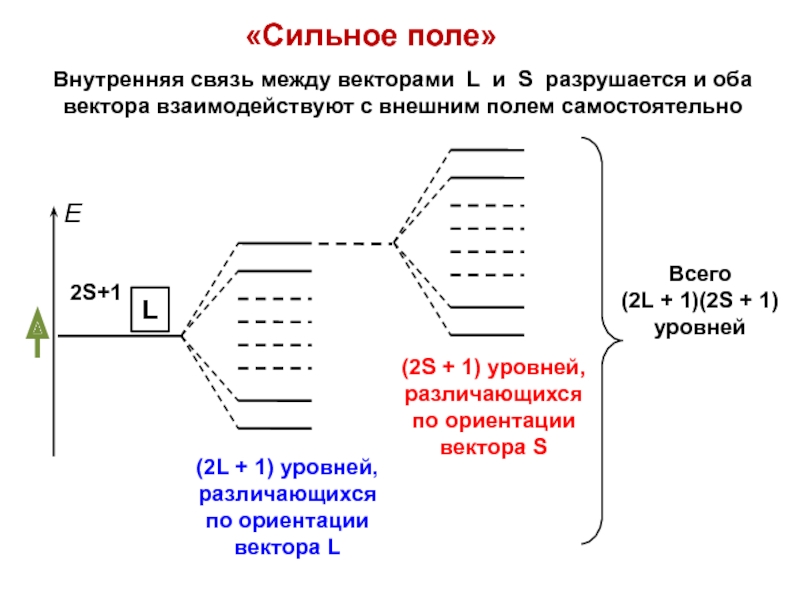
- 67. «Сильное поле»Внутренняя связь между векторами L и
- 68. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Физический атом
Энергия
ААС (атомная абсорбционная спектроскопия)
АЭС (атомная эмиссионная спектроскопия)
РФЭС
(рентгеновская фотоэлектронная спектроскопия)
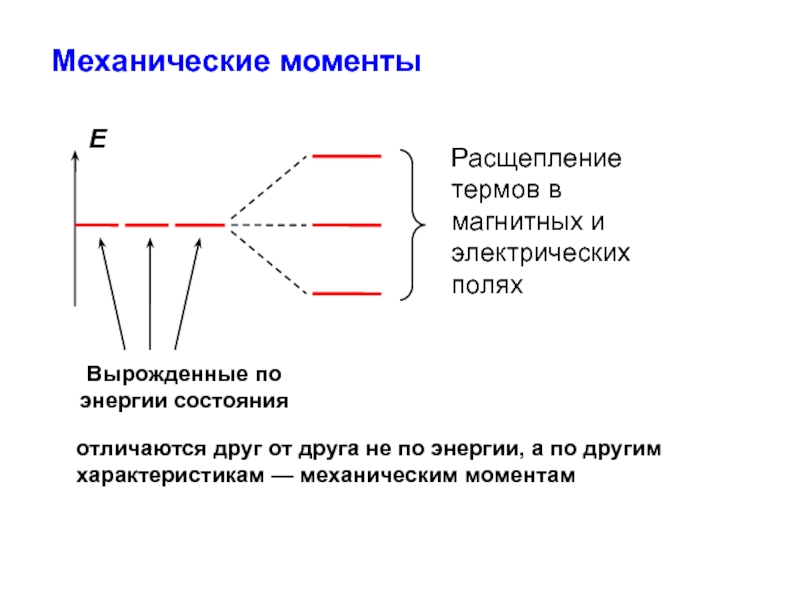
Слайд 3Механические моменты
отличаются друг от друга не по энергии, а
по другим характеристикам — механическим моментам
Слайд 5Орбитальный механический момент
Полный механический момент
Спиновой механический момент
J, L, S —
квантовые числа моментов
МJ, МL, МS — магнитные квантовые числа моментов
Слайд 8Глобальная волновая функция
H Φ = E ⋅ Φ
Φ(x1, y1, z1,
η1, x2, y2, z2, η2, ... , xn, yn, zn,
ηn)Координатное представление
( η — спиновая координата )
Слайд 9Локальная модель атома
С ГЛОБАЛЬНОЙ точки зрения любой атом может быть
описан стандартным квантово-механическим способом — через волновые функции и наблюдаемые.
При
этом глобальные волновые функции являются собственными функциями КМ-операторов, а значения глобальных наблюдаемых — их собственными значениями. Недостаток: глобальное описание дает нам все характеристики стационарных состояний атома, но не объясняет, почему эти характеристики имеют именно такие значения.
Задача: построить локальную структурную модель, позволяющую априорно предсказывать наблюдаемые свойства атома (структуралистский подход).
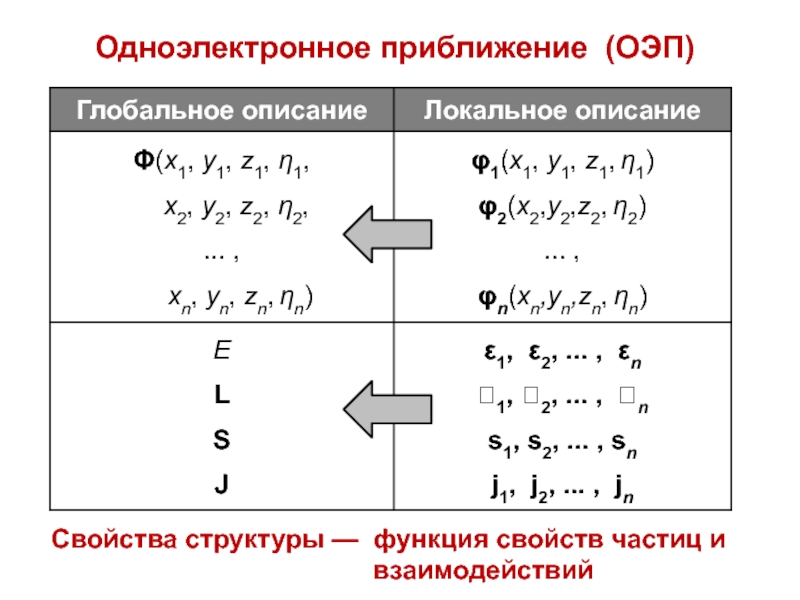
Слайд 10Одноэлектронное приближение (ОЭП)
Свойства структуры — функция свойств частиц и взаимодействий
Слайд 11Одноэлектронное приближение
Каждому электрону приписывается:
индивидуальная функция — «атомная орбиталь» (АО)
φi
(xi, yi, zi, ηi)
набор одноэлектронных наблюдаемых
εi ji
i siφi (xi, yi, zi, ηi) = ψi (xi, yi, zi) ⋅ χi (ηi)
Слайд 12Проблема определения орбиталей и одночастичных наблюдаемых
φi (xi, yi, zi,
ηi) = ?
{ εi ji
i si } = ?
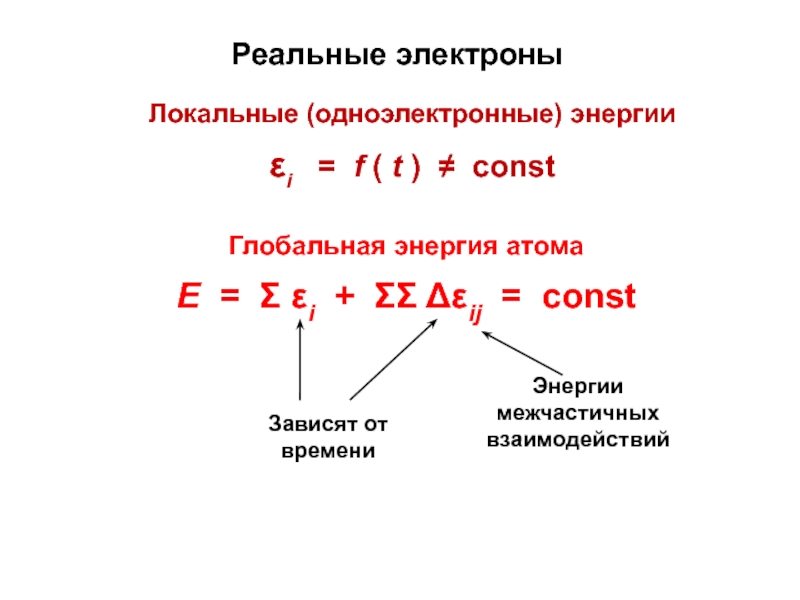
Слайд 15Реальные электроны
Глобальная энергия атома
Е = Σ εi + ΣΣ Δεij
= const
Локальные (одноэлектронные) энергии
εi = f ( t
) ≠ constЗависят от времени
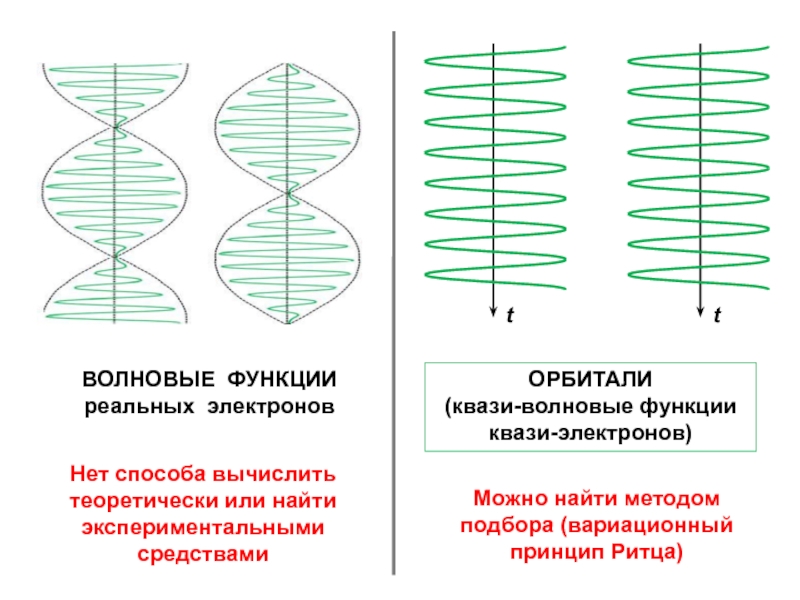
Слайд 17Нет способа вычислить теоретически или найти экспериментальными средствами
Можно найти методом
подбора (вариационный принцип Ритца)
Слайд 18Электроны сами выбирают наиболее простые и экономные способы движения, признаком
которых является минимум полной энергии атома:
E = min
Вариационный принцип
РитцаНеобходимо последовательно решить две задачи:
1) выразить полную энергию как функцию набора орбиталей
Е = Е (φ1 , …, φi , …, φn)
2) найти минимум этой функции
δ Е = 0
Слайд 20Оператор Гамильтона
H = T + Uэя + Uээ
T = t1
⊕ t2 ⊕ … ⊕ tn
Uэя = u1
⊕ u2 ⊕ … ⊕ un Z — зарядовое число ядра; е — элементарный заряд
R — расстояния: между электроном и ядром (RiN),
между двумя электронами (Rij)
Uээ = u11 ⊕ u21 ⊕ u13 ⊕ … ⊕ un,n-1
Слайд 21Пример: атом С (6 электронов)
H = t1 + t2 +
t3 + t4 + t5 + t6 +
+ u1 + u2 + u3 + u4 + u5 + u6 ++ u12 + u13 + u14 + u15 + u16 +
+ u23 + u24 + u25 + u26 +
+ u34 + u35 + u36 +
+ u45 + u46 +
+ u56
Слайд 22hi = [(–2/2m)∇2i – Ze2/RiN ] — одноэлектронный гамильтониан
Uэфф
— «эффективный потенциал», который зависит от вида всех АО, т.е.
Uэфф = f (φ 1, φ 2, ..., φ n)εi — орбитальная энергия
Уравнения Хартри-Фока (ХФ-уравнения)
δЕ = 0
Слайд 23Уравнения Хартри-Фока (ХФ-уравнения)
δЕ = 0
Fi = (hi + Uэфф) —
т.н. «оператор Фока»
АО являются собственными функциями оператора Фока
Каждая из них
описывает один из возможных способов движения электрона (с энергией εi ) в суммарном электрическом поле, создаваемом ядром и всеми остальными электронами (Uэфф). Слайд 24Система уравнений Хартри-Фока требует особого подхода. Ее можно решить, если
известен вид операторов — { hi } и Uэфф.
Трудность
заключается в том, что вид эффективного потенциала зависит от тех функций, которые и требуется найти в качестве решения.Другими словами, нужно знать решение прежде, чем мы приступим к его нахождению.
ИТЕРАЦИОННЫЙ МЕТОД
Слайд 25 (φ1, φ2, ... , φn)о →
(Uэфф)о → уравнения ХФ →
→ (φ1, φ2, ... , φn)1
→ (Uэфф)1 → уравнения ХФ →→ (φ1, φ2, ... , φn)2 → (Uэфф)2 → уравнения ХФ →
→ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . →
→ (φ1, φ2, ... , φn)n → (Uэфф)n → уравнения ХФ →
→ (φ1, φ2, ... , φn)* → (Uэфф)*
Итерационная процедура
(φ1, φ2, ... , φn)о — пробный набор (например, волновые функции атома Н)
Слайд 27Принципиальное различие:
оператор потенциальной энергии в уравнении для атома водорода
обладает сферической симметрией, т.е определяется только расстоянием от электрона до
ядра, независимо от углов θ и ϕ :В случае многоэлектронных атомов оператор потенциальной энергии включает дополнительное слагаемое (Uэфф), величина которого определяется не только расстоянием от электрона до ядра, но и значениями углов θ и ϕ :
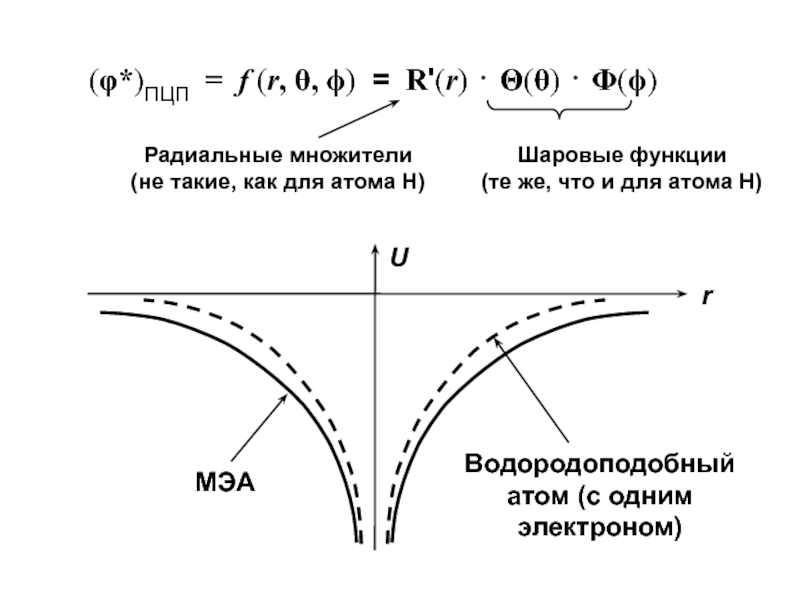
Слайд 28Зависимость Uэфф от углов θ и ϕ не позволяет разделить
трехмерную задачу Фока на три одномерные (как это делается в
случае задачи об атоме водорода) и выразить самосогласованные ХФ-АО в аналитической форме:φ* = f (r, θ, ϕ) ≠ R(r) ⋅ Θ(θ) ⋅ Φ(ϕ)
Приближение центрального поля (ПЦП)
Усредненное по углам ССП
Слайд 30В многоэлектронном атоме сила притяжения электрона к ядру существенно ослаблена
действием остальных электронов —
— «эффект экранирования»
Эффект экранирования сказывается и
на виде орбитали φ*, и на величине орбитальной энергии ε*. Слайд 31n — главное квантовое число, нумерующее радиальную функцию,
(n –
δ) = n* — т.н. «эффективное» главное квантовое число,
ρ =
r /aо — расстояние до ядра, измеренное в атомных единицах длины (ао), Z — зарядовое число ядра,
S — константа экранирования,
Z – S = Z* — эффективный заряд ядра.
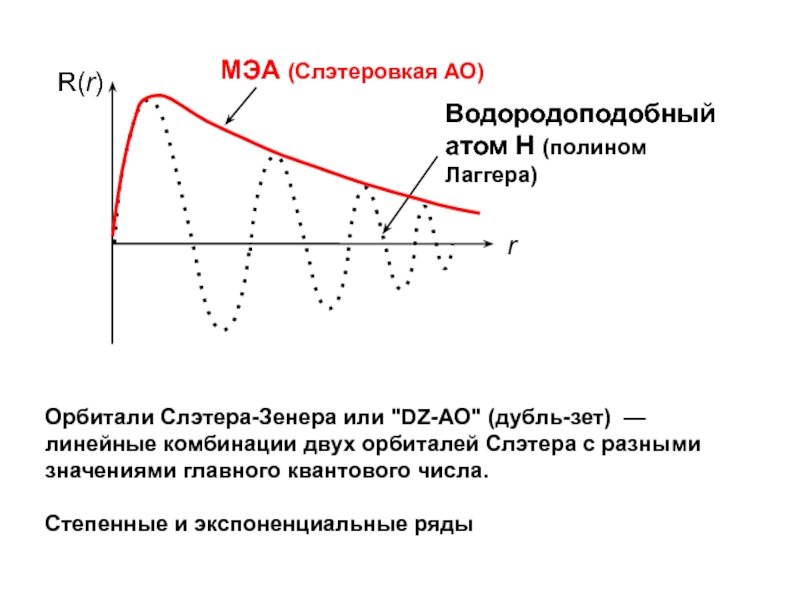
Слэтеровские АО (орбитали Слэтера)
Слайд 32Эффективный заряд ядра Z* = Z – S
Эффективное главное квантовое
число n* = n – δ
ε ≈ – 13,6 (Z*)2/(n*)2
эВНаиболее вероятное расстояние 1s-электрона от ядра (R*)
Слайд 33Орбитали Слэтера-Зенера или "DZ-АО" (дубль-зет) — линейные комбинации двух орбиталей
Слэтера с разными значениями главного квантового числа.
Степенные и экспоненциальные
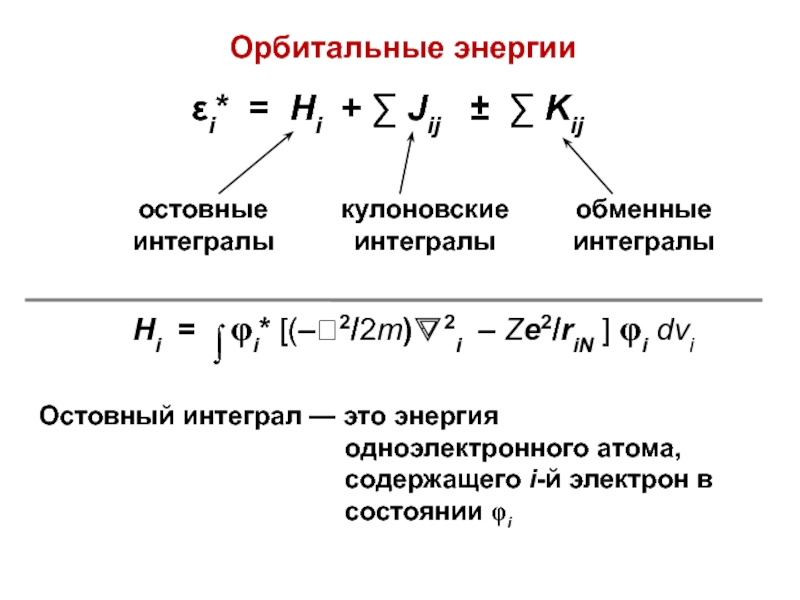
рядыСлайд 34εi* = Hi + ∑ Jij ± ∑ Kij
Орбитальные
энергии
Остовный интеграл — это энергия одноэлектронного атома, содержащего i-й электрон
в состоянии φi Слайд 37Оболочечная модель МЭА
1. Одноэлектронное приближение:
каждому электрону соответствует индивидуальное состояние.
2.
Приближение центрального поля:
индивидуальные состояния электронов в МЭА похожи на
состояния в атоме водорода и их можно охарактеризовать стандартными наборами квантовых чисел:{ n, , m, s, ms }
имеющих те же допустимые значения, что и в атоме водорода.
Слайд 38Каждому электрону соответствует стандартный набор наблюдаемых, выражаемых через квантовые числа:
Орбитальный механический момент
Спиновой механический момент
Орбитальная энергия
ε = f (n)
Слайд 40Электронная конфигурация — способ распределения электронов по состояниям
(1s)ν1 (2s)ν2
(2p)ν3 (3s)ν4 (3p)ν5 (3d)ν6 …
Среди всех конфигураций существует одна —
с наименьшей полной энергией. Она называется ОСНОВНОЙ.
Все остальные конфигурации — ВОЗБУЖДЕННЫЕ.
Возбужденные конфигурации — короткоживущие (около 10–8 с) и, как правило, не представляют интереса для химии.
Слайд 41Основная проблема оболочечной модели — нахождение устойчивых основных конфигураций для
каждого МЭА.
Решение: для каждой конфигурации решается задача Хартри-Фока и выбирается
конфигурация с наименьшей полной энергией.Приближенный вариант: правило Клечковского
С: 1s22s22p2 S: 1s22s22p63s23p4
Mo: 1s22s22p63s23p64s23d104p65s14d5
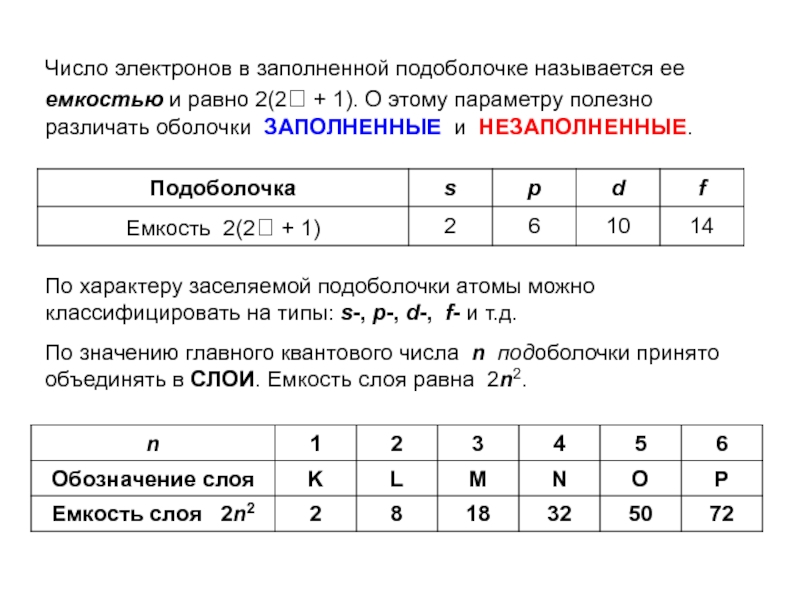
Слайд 43Число электронов в заполненной подоболочке называется ее емкостью и равно
2(2 + 1). О этому параметру полезно различать оболочки ЗАПОЛНЕННЫЕ
и НЕЗАПОЛНЕННЫЕ.По характеру заселяемой подоболочки атомы можно классифицировать на типы: s-, p-, d-, f- и т.д.
По значению главного квантового числа n подоболочки принято объединять в СЛОИ. Емкость слоя равна 2n2.
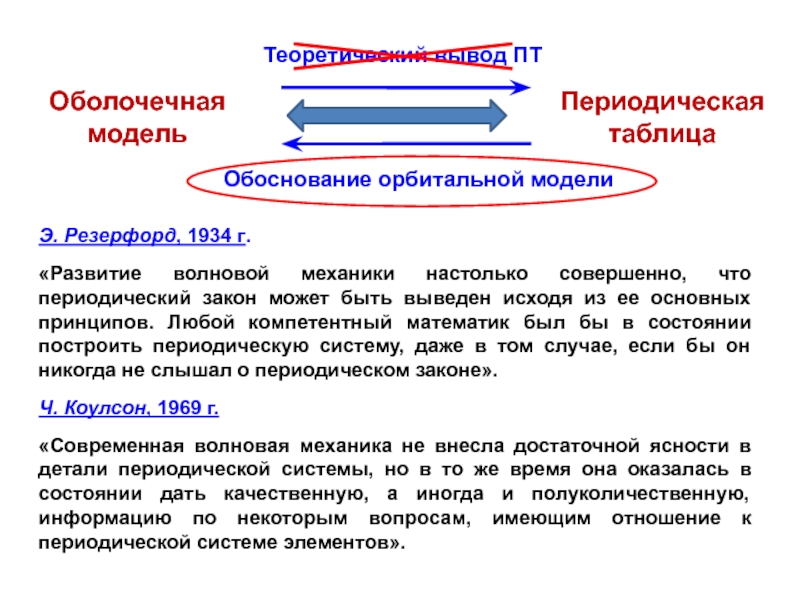
Слайд 45Э. Резерфорд, 1934 г.
«Развитие волновой механики настолько совершенно, что
периодический закон может быть выведен исходя из ее основных принципов.
Любой компетентный математик был бы в состоянии построить периодическую систему, даже в том случае, если бы он никогда не слышал о периодическом законе».Ч. Коулсон, 1969 г.
«Современная волновая механика не внесла достаточной ясности в детали периодической системы, но в то же время она оказалась в состоянии дать качественную, а иногда и полуколичественную, информацию по некоторым вопросам, имеющим отношение к периодической системе элементов».
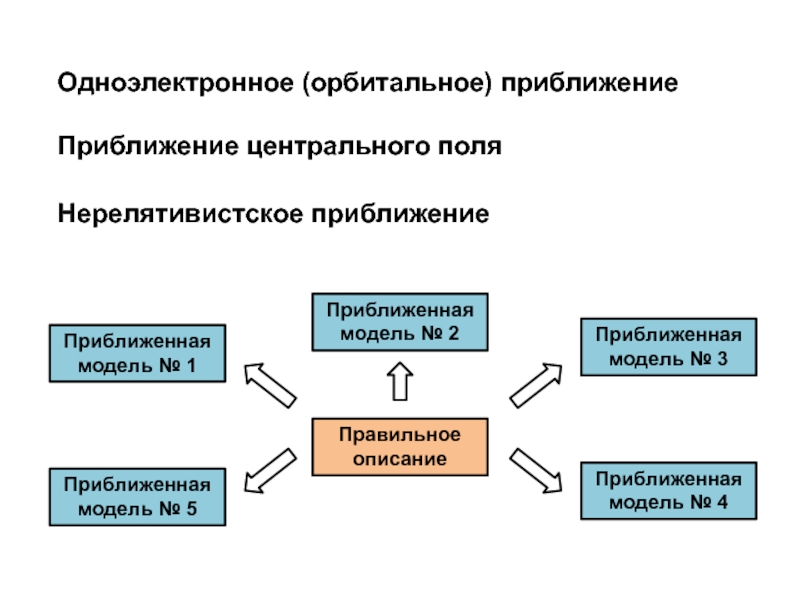
Слайд 46Одноэлектронное (орбитальное) приближение
Нерелятивистское приближение
Приближение центрального поля
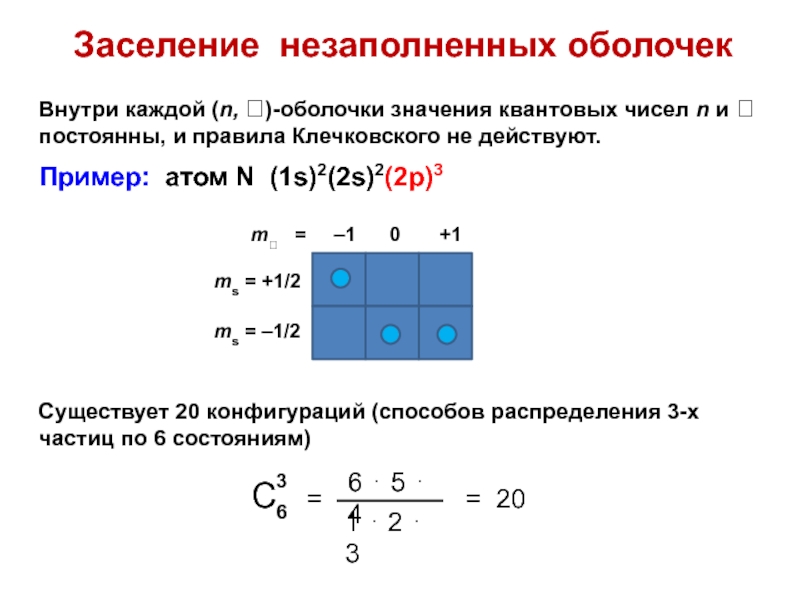
Слайд 47Заселение незаполненных оболочек
Внутри каждой (n, )-оболочки значения квантовых чисел
n и постоянны, и правила Клечковского не действуют.
Пример: атом
N (1s)2(2s)2(2p)3Существует 20 конфигураций (способов распределения 3-х частиц по 6 состояниям)
Слайд 48Поскольку орбитальные энергии всех 2р-АО одинаковы, на полную энергию атома
оказывают влияние небольшие вклады, связанные с различиями в силах межэлектронного
отталкивания и спин-орбитального взаимодействия.Для оценки величины этих вкладов требуется установить значения характеристик глобальных векторов орбитального и спинового моментов:
| L | 2 = 2 ⋅ L(L + 1) и LZ = ⋅ ML
| S | 2 = 2 ⋅ S(S + 1) и SZ = ⋅ MS
L = ? ML = ?
S = ? MS = ?
Слайд 491. LS-приближение, справедливое для легких атомов (Z < 20).
Сложение производится
отдельно для орбитальных и отдельно для спиновых моментов:
L = 1
+ 2 + . . . + n S = s1 + s2 + . . . + snЗатем глобальные моменты складываются и образуют вектор полного механического момента атома:
J = L + S
Две основные схемы вычисления глобальных моментов
2. jj-приближение, справедливое для тяжелых атомов
Сначала складываются локальные орбитальный и спиновой моменты, образуя локальный (одноэлектронный) вектор полного механического момента, а затем локальные моменты складываются в глобальный:
ji = i + si J = j1 + j2 + . . . + jn
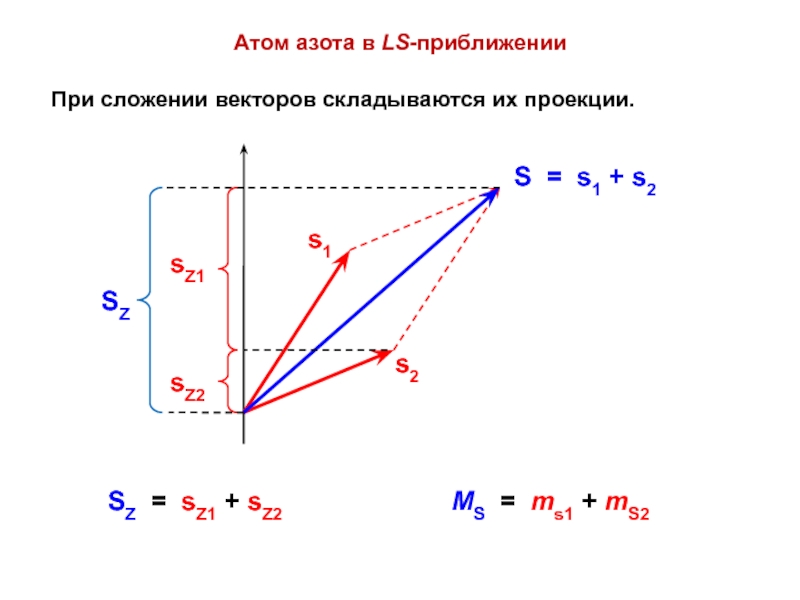
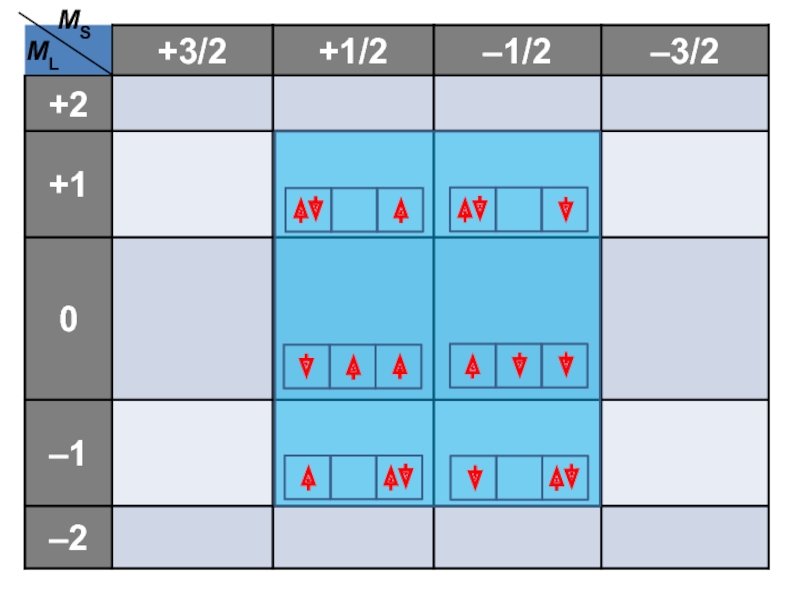
Слайд 50При сложении векторов складываются их проекции.
Атом азота в LS-приближении
SZ
= sZ1 + sZ2
MS = ms1 + mS2
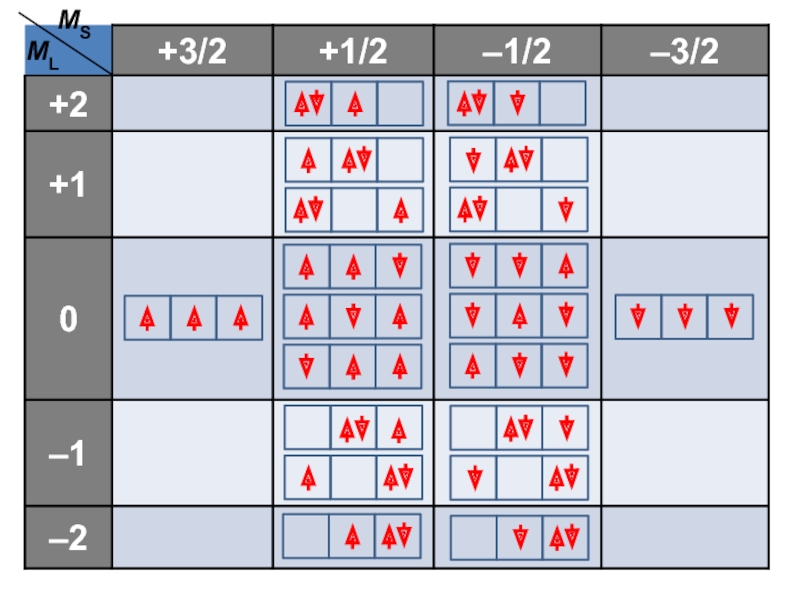
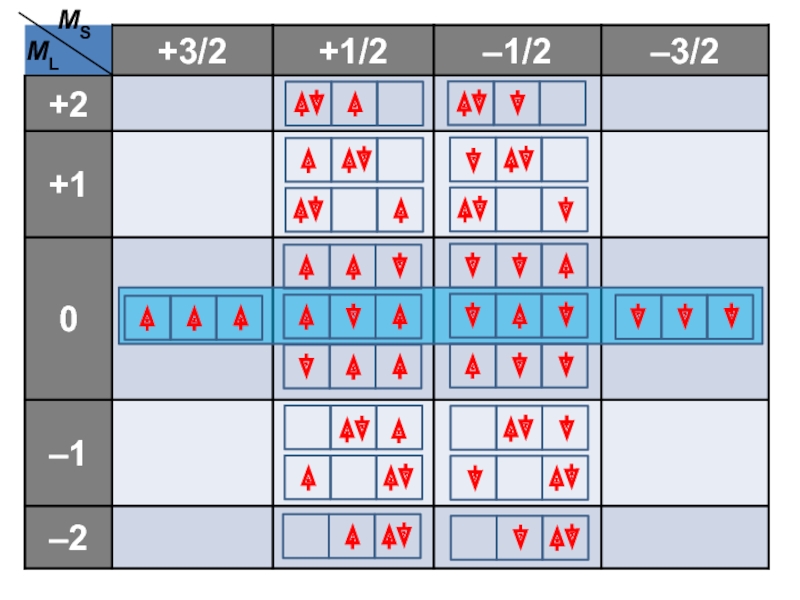
Слайд 51Длина проекции глобального вектора определяется суммой магнитных чисел локальных векторов:
ML
= m1 + m2 + m3
MS = ms1 + ms2 + ms3Зная величины проекций векторов L и S , можно легко найти и их длины (модули), поскольку выполняется правило:
ML = L, (L – 1), ... , (1 – L), – L
MS = S, (S – 1), ... , (1 – S), –S
Для систематического анализа построим специальную таблицу, в которую и будем помещать возможные конфигурации атома с определенными значениями квантовых чисел ML и MS.
Слайд 60Зная принадлежность состояний к определенным термам, можно предсказать их распределение
по энергетической шкале.
Правила Хунда:
1 правило: минимальной энергией обладает терм с
максимальной мультиплетностью (значением квантового числа S).2 правило: при равных мультиплетностях минимальной энергией обладает терм с максимальным квантовым числом L.
Для атома азота минимальной энергией будут обладать 4 состояния терма 4S, а максимальной — 6 состояний терма 2P.
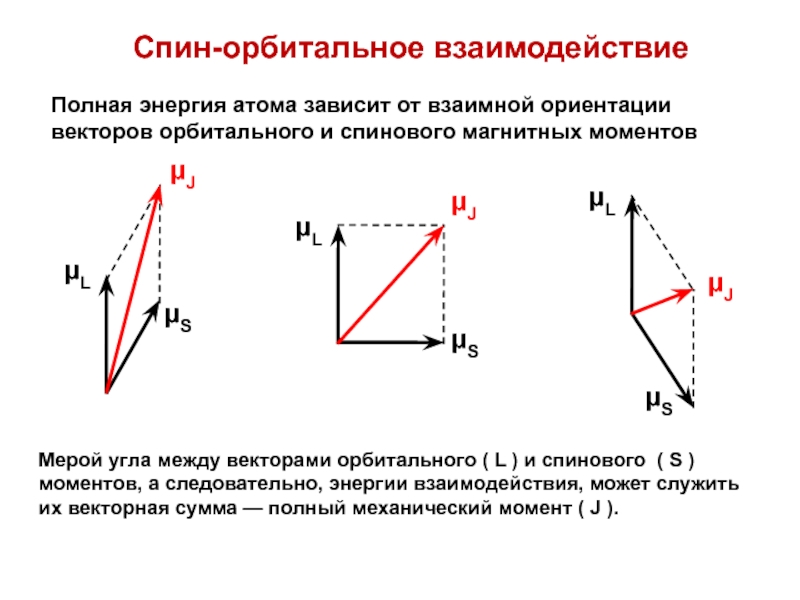
Слайд 62Спин-орбитальное взаимодействие
Полная энергия атома зависит от взаимной ориентации векторов орбитального
и спинового магнитных моментов
Мерой угла между векторами орбитального ( L
) и спинового ( S ) моментов, а следовательно, энергии взаимодействия, может служить их векторная сумма — полный механический момент ( J ). Слайд 63Вычисление величины полного момента
| J |2 = 2 [J(J +
1)]
J = (L + S), (L + S – 1),
… , | L – S | L = 0
S = 3/2
L = 1
S = 1/2
L = 2
S = 1/2
4S
2P
2D
J = 3/2
J1 = 1 + 1/2 = 3/2
J2 = 1 – 1/2 = 1/2
J1 = 2 + 1/2 = 5/2
J2 = 2 – 1/2 = 3/2
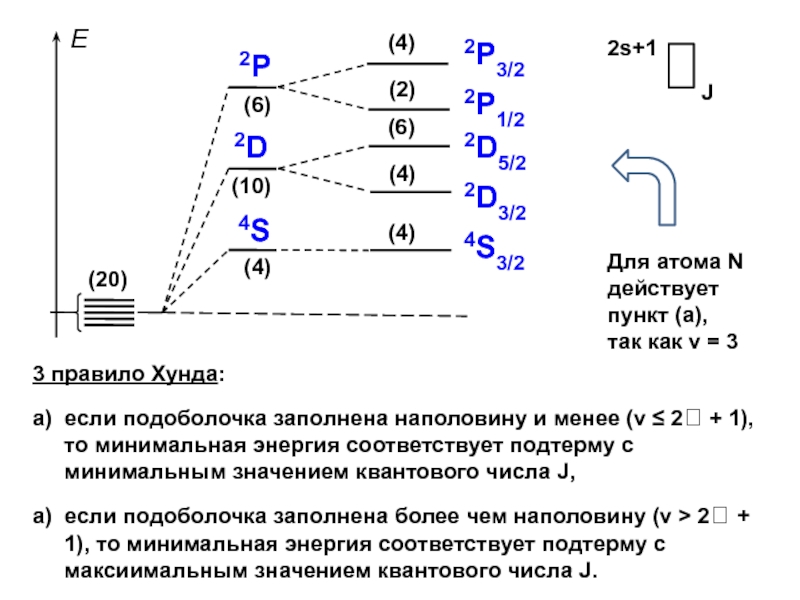
Слайд 643 правило Хунда:
а) если подоболочка заполнена наполовину и менее (ν
≤ 2 + 1), то минимальная энергия соответствует подтерму с
минимальным значением квантового числа J,а) если подоболочка заполнена более чем наполовину (ν > 2 + 1), то минимальная энергия соответствует подтерму с максиимальным значением квантового числа J.
Для атома N действует пункт (а),
так как ν = 3
















![Атомы hi = [(–2/2m)∇2i – Ze2/RiN ] — одноэлектронный гамильтониан Uэфф — hi = [(–2/2m)∇2i – Ze2/RiN ] — одноэлектронный гамильтониан Uэфф — «эффективный потенциал», который зависит от вида](/img/thumbs/8c4d5917077435c6c40d8faa2d375b3b-800x.jpg)























![Атомы Вычисление величины полного момента| J |2 = 2 [J(J + 1)]J Вычисление величины полного момента| J |2 = 2 [J(J + 1)]J = (L + S), (L +](/img/thumbs/a3b91f933122b9c3b41310346efd6450-800x.jpg)