Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Автор: Виноградова Светлана Анатольевна логарифмическая функция, её свойства и
Содержание
- 1. Автор: Виноградова Светлана Анатольевна логарифмическая функция, её свойства и
- 2. Содержание Сведения из историиПонятие логарифмаСвойства логарифмовПримерыПонятие функции
- 3. Сведения из истории.Потребность в сложных расчётах в
- 4. В 1614 году шотландский математик-любитель Джон Непер
- 5. Сведения из историиЛогарифмы необычайно быстро вошли в
- 6. Слайд 6
- 7. Понятие логарифма.Логарифмом положительного числа b по положительному
- 8. Примерыlog2 8 =log3 729 =log0,2 25 =log4
- 9. loga bm =logak bm =loga b =loga
- 10. Понятие логарифмической функции.Функцию вида y = logaх,
- 11. а) При а > 1 функция выпукла
- 12. График логарифмической функции y = logах,
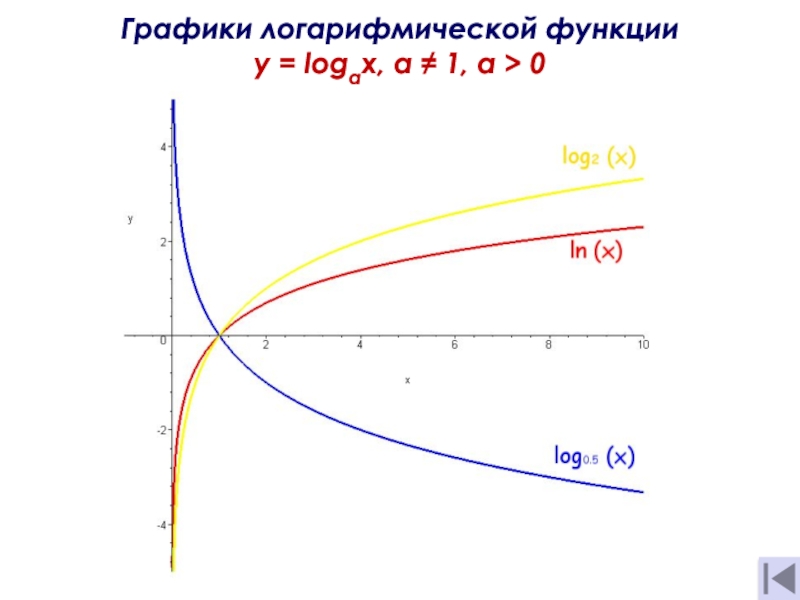
- 13. Графики логарифмической функции y = logах, а ≠ 1, a > 0
- 14. Если а > 1 и 0 <
- 15. Логарифмические уравненияУравнения вида loga f(x) = logа
- 16. Логарифмические уравнения. Примеры Пример 1Пример 2Ответ: -3.
- 17. Пример 3Логарифмические уравнения. Примеры x = 2Ответ: 2.
- 18. Пример 4Логарифмические уравнения. Примеры Ответ: 100.
- 19. Пример 5Логарифмические уравнения. Примеры
- 20. Пример 5Логарифмические уравнения. Примеры
- 21. Пример 6Логарифмические уравнения. Примеры Ответ: 0,2; 25.Т.к.
- 22. Пример 7Логарифмические уравнения. Примеры
- 23. Пример 8Логарифмические уравнения. Примеры
- 24. Логарифмические неравенстваНеравенства вида loga f(x) > logа
- 25. Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4].
- 26. Пример 3Пример 4Логарифмические неравенства. ПримерыОтвет: (0; 5) ∪ (40; 45).
- 27. Логарифмические неравенства. ПримерыПример 5Ответ: (2; 3)∪(3,375; 4) .x ∈ (2; 3)x ∈ (3,375; 4)
- 28. Используемые материалыАлгебра и начала анализа. 11 класс.
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Автор: Виноградова Светлана Анатольевна
логарифмическая функция,
её свойства и график
МОУ «СОШ №
61» г.Саратов
Слайд 2Содержание
Сведения из истории
Понятие логарифма
Свойства логарифмов
Примеры
Понятие функции у = logax
Свойства
логарифмической функции
График логарифмической функции
Свойства сравнения логарифмов
Логарифмические уравнения
Логарифмические неравенства
Слайд 3Сведения из истории
.
Потребность в сложных расчётах в XVI веке быстро
росла, и значительная часть трудностей была связана с умножением и
делением многозначных чисел, а также извлечением корней. В конце века нескольким математикам, почти одновременно, пришла в голову идея: заменить трудоёмкое умножение на простое сложение, сопоставив с помощью специальных таблицгеометрическую и арифметическую прогрессии, при этом геометрическая будет исходной. Тогда и деление автоматически заменяется на неизмеримо более простое и надёжное вычитание, а извлечение корня степени n сводится к делению логарифма подкоренного выражения на n. Первым эту идею опубликовал в своей книге «Arithmetica integra» Михаэль Штифель, который, впрочем, не приложил серьёзных усилий для реализации своей идеи.
Слайд 4В 1614 году шотландский математик-любитель Джон Непер опубликовал на латинском
языке сочинение под названием «Описание удивительной таблицы логарифмов». В нём
было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'. Термин логарифм, предложенный Непером, утвердился в науке. Теорию логарифмов Непер изложил в другой своей книге «Построение удивительной таблицы логарифмов», изданной посмертно в 1619 году его сыном.Сведения из истории
Слово логарифм происходит от греческого λόγοφ (число) и αρινμοφ (отношение) и переводится, следовательно, как отношение чисел.
«Логарифм данного синуса есть число, которое арифметически возрастало всегда с той же скоростью, с какой полный синус начал геометрически убывать».
Слайд 5Сведения из истории
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов
не ограничились разработкой новой теории. Было создано практическое средство –
таблицы логарифмов, – резко повысившее производительность труда вычислителей. Добавим, что уже в 1623 г., т. е. всего через 9 лет после издания первых таблиц, английским математиком Д. Гантером была изобретена первая логарифмическая линейка, ставшая рабочим инструментом для многих поколений.Первые таблицы логарифмов составлены независимо друг от друга шотландским математиком Дж. Непером (1550 - 1617) и швейцарцем И. Бюрги (1552 - 1632).
Слайд 7Понятие логарифма
.
Логарифмом положительного числа b по положительному и отличному от
1 основанию а называют показатель степени, в которую нужно возвести
число а, чтобы получить число blogab = c, ac = b; а ≠ 1, a > 0, b > 0
- основное логарифмическое тождество
Слайд 8Примеры
log2 8 =
log3 729 =
log0,2 25 =
log4 8 =
log2 2
=
log10 1 =
log49 1/7 =
log0,1 10000 =
3, 23 = 8;
6, 36 = 729;
-2, (0,2)-2 = 25;
1,5, 41,5 = 8;
1, 21 = 2;
0, 100 = 1;
-0,5, 49-0,5 = 1/7;
-4, 0,1-4 = 10000.
Слайд 9loga bm =
logak bm =
loga b =
loga b =
loga b
∙ logc d =
=
alogcb =
Основные свойства логарифмов
loga 1 =
loga a =
loga =
logak a =
loga am =
logak am =
loga bc =
loga =
logak b =
0;
1;
m;
m logab;
logab + logac;
logab − logaс;
-1;
logc b ∙ loga d
blogca
Слайд 10Понятие логарифмической функции
.
Функцию вида
y = logaх, где а ≠
1, a > 0, х > 0
называют
логарифмической функцией
Слайд 11а) При а > 1 функция выпукла вверх;
б) при 0
< а < 1 функция выпукла вниз.
а) При а >
1 функция возрастает на (0; +∞);б) при 0 < а < 1 функция убывает на (0; +∞).
а) Нули функции: у = 0 при х = 1;
б) точек пересечения с осью ординат нет.
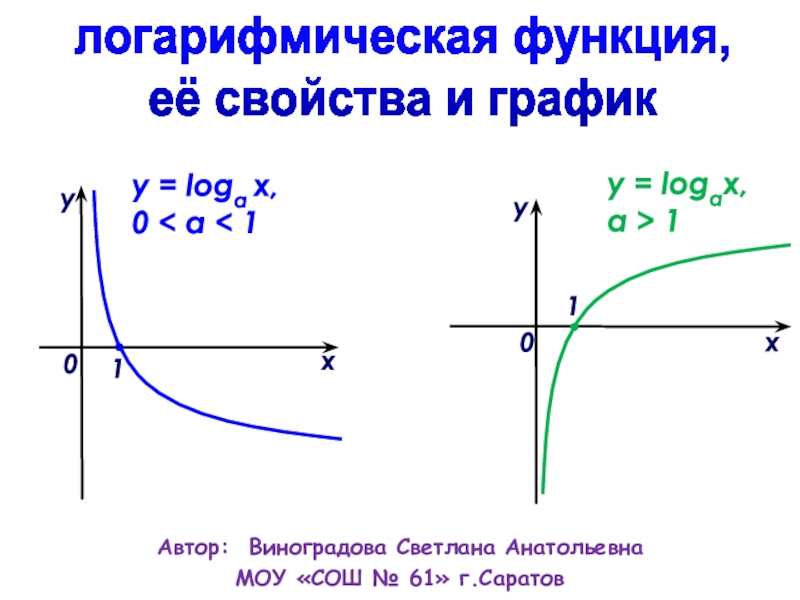
Свойства логарифмической функции y = logах, а ≠ 1, a > 0
Ни четная функция, ни нечетная.
D(y) = (0; +∞),
E(y) = (-∞; +∞).
Не ограничена сверху, не ограничена снизу.
Не имеет ни наибольшего, ни наименьшего значений.
Непрерывна.
Ось у является вертикальной асимптотой графика логарифмической функции.
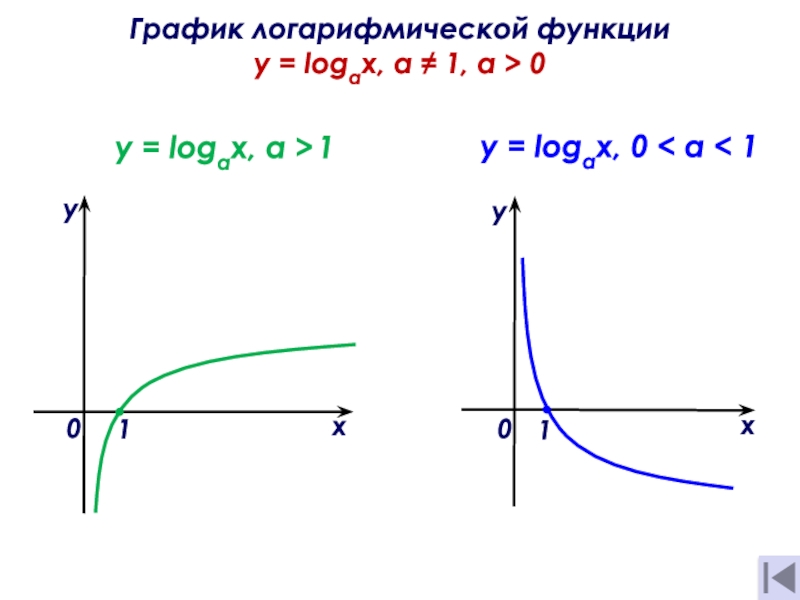
Слайд 12График логарифмической функции y = logах, а ≠ 1, a
> 0
х
у
0
y = logaх, а > 1
1
y = logах, 0
< а < 1х
у
0
1
Слайд 14Если а > 1 и 0 < x1 < x2,
то loga x1 < loga x2 .
Свойства сравнения логарифмов при
а ≠ 1, a > 0Если 0 < а < 1 и 0 < x1 < x2, то loga x1 > loga x2 .
Если 1< а < b и x > 1, то loga x > logb x .
logab > 0 ⟺ a > 0, b > 0 и (a – 1)(b – 1) > 0 (если положительные числа a и b лежат “по одну сторону от единицы”)
Если 0 < а < b < 1 и x > 1, то loga x > logb x .
Если 1< а < b и 0 < x < 1, то loga x < logb x .
Если 0 < а < b < 1 и 0 < x < 1, то loga x < logb x .
logab < 0 ⟺ a > 0, b > 0 и (a – 1)(b – 1) < 0 (если положительные числа a и b лежат “по разные стороны от единицы”)
Слайд 15Логарифмические уравнения
Уравнения вида loga f(x) = logа h(х), где а
≠ 1, a > 0
называют логарифмическими уравнениями
loga f(x)
= loga h(х)⟺
Методы решения логарифмических уравнений:
Функционально-графический метод.
Метод потенцирования.
Метод введения новой переменной.
Слайд 21Пример 6
Логарифмические уравнения. Примеры
Ответ: 0,2; 25.
Т.к. обе части равенства
принимают только положительные значения, прологарифмируем их по основанию 5:
Слайд 24Логарифмические неравенства
Неравенства вида loga f(x) > logа g(х), где а
≠ 1, a > 0
называют логарифмическими неравенствами
loga f(x) >
logа g(х)0 < а < 1
а > 1
или
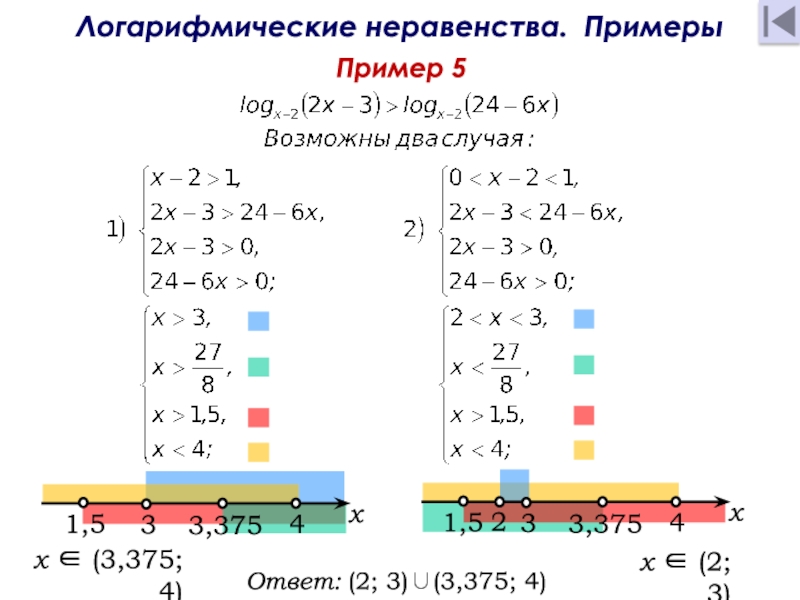
Слайд 27Логарифмические неравенства. Примеры
Пример 5
Ответ: (2; 3)∪(3,375; 4) .
x ∈ (2;
3)
x ∈ (3,375; 4)
Слайд 28Используемые материалы
Алгебра и начала анализа. 11 класс. В 2 ч.
Ч. 1. Учебник для общеобразоват. учреждений (профильный уровень) / А.Г.
Мордкович, П.В. Семенов. 2-е изд., стер. – М.: Мнемозина, 2008http://ru.wikipedia.org/wiki - логарифмические линейки
http://ru.wikipedia.org/wiki - логарифм
Комплексный логарифм
(мнимая часть)





















![Автор: Виноградова Светлана Анатольевна
логарифмическая функция,
её свойства и Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4]. Логарифмические неравенства. ПримерыПример 1Пример 2Ответ: (6; 14).Ответ: [0; 4].](/img/tmb/7/609502/5aea3abff1d97cd2612147dde2c6c6c9-800x.jpg)