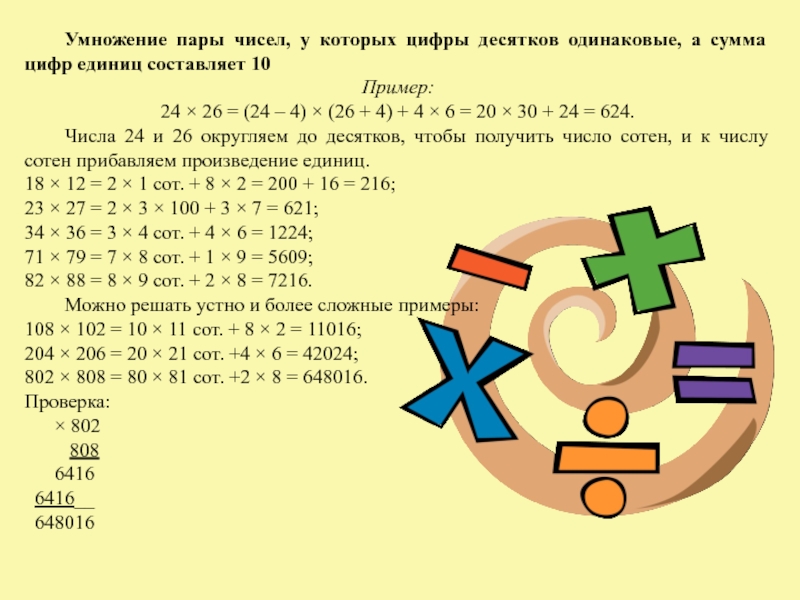Быстрый счёт без калькулятора. Приемы быстрого счета

просто необходимо владеть основными приемами быстрого счета.
Рассмотрим некоторые способы

быстрого устного счета, которые рассчитаны на ум "обычного" человека и не требуют уникальных способностей.

к числу 9, прибавьте к нему 10 и отнимите 1;

чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д.
Например, 56+8=56+10-2=64;
65+9=65+10 -1=74.

больше5, то число необходимо округлить в сторону увеличения, а затем

вычесть ошибку округления из полученной суммы.
Если же цифра единиц меньше, то прибавляем сначала десятки, а потом единицы.
Например, 34+48=34+50 – 2 = 82;
27+31=27+30+1 =58.

потом десятки, а затем единицы.
Например, 359+523= 300+500+50+20+9+3=
=800 +70

+12 = 882;
456+298=400+200+50+90+6+8=600+140+14=754.

затем подкорректируйте полученный ответ.
Например, 56 – 9 = 56 –

10 + 1 = 47;
436 – 87 = 436 - 100 + 13 = 349.

простым правилом:
Отнимите от 9 все цифры, кроме последней. А

последнюю цифру отнимите от 10:

Например, 1000 - 648
Шаг1: от 9 отнимите 6 = 3
Шаг2: от 9 отнимите 4 = 5
Шаг3: от 10 отнимите 8 = 2
Ответ: 352

дважды удваивают.
Например, 527 · 4 = (527 · 2) ·

2 = 1054 · 2 = 2108.

Чтобы число разделить на 4 , его дважды делят на 2.
Например, 2648 : 4 = (2648 : 2) : 2 = 1324 : 2 = 662.

его умножить на 10 и разделить на 2.
Например, 348 ·

5= (348 · 10) : 2 = 3480 : 2 = 1740.

Чтобы число разделить на 5, нужно умножить его на 0,2, то есть в удвоенном исходном числе отделить запятой последнюю цифру.
Например, 51 : 5 = 51 · 0,2 = 10,2.

на число, оканчивающееся на 5, следует применить правило: если один

из сомножителей увеличить в несколько раз, а другой – уменьшить во столько же раз, произведение не изменится.
Например,
44 · 5 = (44 : 2) · 5 · 2 = 22 · 10 = 220;
26 · 35 = (26 : 2) · 35 · 2 = 13 · 70 = 910;
36 · 45 = (36 : 2) · 45 · 2 = 18 · 90 = 1625;
18 · 65 = (18 : 2) · 65 · 2 = 9 · 130 = 1170;
12 · 75 = (12 : 2) · 75 · 2 = 6 · 150 = 900;
14 · 85 = (14 : 2) · 85 · 2 = 7 · 170 = 1190;
12 · 95 = (12 : 2) · 95 · 2 = 6 · 190 = 1140.
При умножении на 65, 75, 85, 95 числа следует брать небольшие, в пределах второго десятка. В противном случае вычисления усложнятся.

на 100/4, то есть умножить на 100 и разделить на

4.
Например, 348 · 25 = (348 · 100) : 4 = (34800 : 2) : 2 = 17400 : 2 = 8700.

Умножение на 1,5.

Чтобы умножить число на 1,5 нужно к исходному числу прибавить его половину.
Например, 228 · 1,5 = 228 + 114 = 342.

на 9, посмотрите на руки.
Загните палец, который соответствует умножаемому

числу (например 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7). Ответ: 27.

0 и отнимают исходное число.
Например, 847 · 9 =

8470 – 847 = 7623.

и вычтем из множимого.

2. К результату приписываем дополнение цифры единиц

множимого до 10.
Например, 576 · 9
1. 576 – (57+1)=518
2. 10 - 6 =4
Ответ: 5184
379 · 9
1. 379 – (37 + 1) =341
2.10 - 9 = 1
Ответ: 3411

на 1.

2. Находим дополнение числа, образованного двумя последними цифрами до

100.

3. Приписываем дополнение к предшествующему результату.
Пример:
27 · 99 134 · 99
27 – 1 = 26 (сотен – 0+1) 134 – 2 = 132 (сотня – 1 + 1)
100 - 27 = 73 100 – 34 = 66
27 · 99 = 2673 134 · 99 = 13266

нему приписывают 0 и прибавляют исходное число.
Например, 243 · 11

= 2430 + 243 = 2673.

2 способ. Если хочешь умножить число на 11, то поступай так: запиши число, которое нужно умножить на 11, а между цифрами исходного числа вставь сумму этих цифр.
Если сумма получается двузначное число, то 1 прибавляем к первой цифре исходного числа.
Например, 45 · 11 = 4 (4+5)7= 967.

каждую цифру и прибавлять к ней поочередно ее «соседа».
Например, 63247

· 12
Необходимо записывать цифры множимого через интервал и каждую цифру результата писать точно под цифрой числа 63247, из которой она образовалась.
63247 · 12  дважды 7 будет = 14, переносим 1
4
63247 · 12  дважды 4 + 7 + 1 = 16, переносим 1
64
63247 · 12  дважды 2 + 4 + 1 = 9
964
Следующие шаги аналогичны.
Окончательный ответ : 63247 · 12= 758964.

на 22, 33, …, 99, надо этот множитель представить в

виде произведения однозначного числа на 11, то есть 44 = 4 · 11; 55 = 5 · 11.
Затем произведение первых чисел умножить на 11:

Например, 24 · 22 = 24 · 2 · 11 = 48 · 11 = 528
23 · 66 =23 · 6 · 11=138 · 11=1518

первый множитель на число его сотен и приписываем к нему

справа две последние цифры первого множителя.
Например, 125 · 101 = 126(125+1)25 =12625
Этот прием дети легко усваивают при записи вычисления в столбик.
х125
101
+ 125
125
12625

число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков

(6) на число десятков, увеличенное на 1 (на 6+1 = 7), и к полученному числу приписывают 25
(6 · 7)25 = 4225
Например: 952 =(9 · 10)25= 9025; 1252 = (12 · 13)25=15625
Возведение в квадрат числа, близкого к 50.
Если хочешь возвести в квадрат число, близкое к 50, но большее 50, то поступай так:
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат избытка данного числа над 50.
Примеры:
1) 582 = 3364. Объяснение: 58 – 25 = 33, 58-50=8, 82 = 64, 582 = 3364.
2) 672 = 4489. Объяснение: 67 – 25 = 42, 67 – 50 = 17, 172 =289, 672 = 4200 + 289 = = 4489.
Если хочешь возвести в квадрат число, близкое к 50, но меньшее 50, то поступай так:
1) вычти из этого числа 25;
2) припиши к результату двумя цифрами квадрат недостатка данного числа до 50.
Примеры:
1) 482 = 2304. Объяснение: 48 – 25 = 23, 50 – 48 =2, 22 = 4, 482 = 2304.
2) 372 = 1369. Объяснение: 37 – 25 = 12,= 13, 132 =169, 372 = 1200 + 169 = 1369.

разделить на 3 и умножить на 111.
Например: 24 · 37

= (24 : 3) · 37 · 3 = 8 · 111 = 888;
27 · 37 = (27 : 3) · 111 = 999.

Деление на 37.
Чтобы число разделить на 37, надо это число разделить на 111 и умножить на 3.
Например: 999 : 37 = 999 :111 · 3 = 27;
888 : 37 = 888 :111 · 3 = 24.

Чтобы научиться устно умножать и делить на 37, надо хорошо знать таблицу умножения на три и признак делимости на три.

надо сначала перемножить цифры десятков, затем цифру десятков умножить на

сумму цифр единиц и, наконец, надо перемножить цифры единиц. Получим ответ.
Например: 12 ×13
Шаг1. 1 × 1 = 1
Шаг 2. 1 × (2+3) = 5
Шаг 3. 2 × 3 = 6
Ответ: 156

цифр единиц составляет 10
Пример:
24 × 26 = (24 – 4)

× (26 + 4) + 4 × 6 = 20 × 30 + 24 = 624.
Числа 24 и 26 округляем до десятков, чтобы получить число сотен, и к числу сотен прибавляем произведение единиц.
18 × 12 = 2 × 1 сот. + 8 × 2 = 200 + 16 = 216;
23 × 27 = 2 × 3 × 100 + 3 × 7 = 621;
34 × 36 = 3 × 4 сот. + 4 × 6 = 1224;
71 × 79 = 7 × 8 сот. + 1 × 9 = 5609;
82 × 88 = 8 × 9 сот. + 2 × 8 = 7216.
Можно решать устно и более сложные примеры:
108 × 102 = 10 × 11 сот. + 8 × 2 = 11016;
204 × 206 = 20 × 21 сот. +4 × 6 = 42024;
802 × 808 = 80 × 81 сот. +2 × 8 = 648016.
Проверка:
× 802
808
6416
6416__
648016

надо сначала перемножить цифры десятков и правее полученного произведения записать

под этим числом сумму цифр десятков, а затем перемножить 1 на 1 и записать еще правее.
Сложив столбиком, получим ответ.
1) 81 × 31 = ?
8 × 3 = 24
8 + 3 = 11
1 × 1 = 1
2511
81 × 31 = 2511
2) 21 × 31 = ?
2 × 3 = 6
2 +3 = 5
1 × 1 = 1
651
21 × 31 = 651
3) 91 × 71 = ?
9 × 7 = 63
9 + 7 = 16
1 × 1 = 1
6461
91 × 71 = 6461

а цифры единиц одинаковые.
Правило. При умножении двузначных чисел. у которых

сумма цифр десятков равна 10, а цифры единиц одинаковые, надо перемножить цифры десятков. и прибавить цифру единиц, получим число сотен и к числу сотен прибавим произведение единиц.
Примеры:
72 × 32 = (7 × 3 + 2)сот. + 2 × 2 = 2304;
64 × 44 = (6 × 4 + 4) × 100 + 4 × 4 = 2816;
53 × 53 = (5 × 5 +3) × 100 + 3 × 3 = 2809;
18 × 98 = (1 × 9 + 8) × 100 + 8 × 8 = 1764;
24 × 84 = (2 × 8 + 4) ×100+ 4 × 4 = 2016;
63 × 43 = (6 × 4 +3) × 100 +3 × 3 = 2709;
35 × 75 = (3 × 7 + 5) × 100 +5 × 5 = 2625.

семью печатями, а научно разработанная система. Раз есть система, значит

ее можно изучать, ей можно следовать, ею можно овладеть.
Все рассмотренные нами методы устного счёта говорят о многолетнем интересе ученых и простых людей к игре с цифрами.
Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, привить интерес к математике, добиться успехов в изучении всех школьных предметов.