Цепи маркова

отчасти рассматриваем мы ее из-за того, что ее изложение не

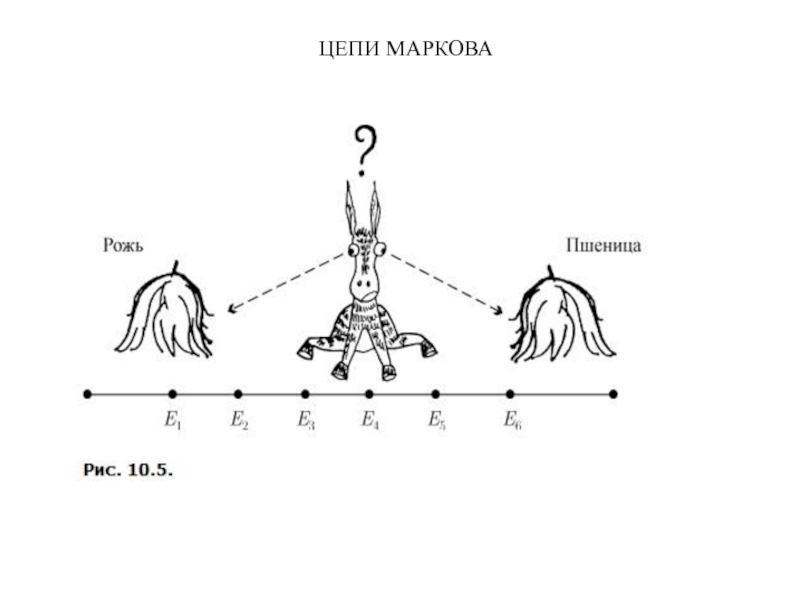
требует введения большого количества новых терминов.
Рассмотрим задачу об осле, стоящем точно между двумя копнами: соломы ржи и соломы пшеницы (рис. 10.5).
Осел стоит между двумя копнами: "Рожь" и "Пшеница" (рис. 10.5). Каждую минуту он либо передвигается на десять метров в сторону первой копны (с вероятностью ), либо в сторону второй копны (с вероятностью ), либо остается там, где стоял (с вероятностью ); такое поведение называется одномерным случайным блужданием. Будем предполагать, что обе копны являются "поглощающими" в том смысле, что если осел подойдет к одной из копен, то он там и останется. Зная расстояние между двумя копнами и начальное положение осла, можно поставить несколько вопросов, например: у какой копны он очутится с большей вероятностью и какое наиболее вероятное время ему понадобится, чтобы попасть туда?

копнами равно пятидесяти метрам и что наш осел находится в

двадцати метрах от копны "Пшеницы". Если места, где можно остановиться, обозначить через ( — сами копны), то его начальное положение можно задать вектором -

я компонента которого равна вероятности того, что он первоначально находится в . Далее, по прошествии одной минуты вероятности его местоположения описываются вектором
, а через две минуты — вектором .

месте по прошествии минут становится затруднительным. Оказалось, что удобнее всего

ввести для этого матрицу перехода

в за одну минуту. Например,

и . Эти вероятности называются вероятностями перехода, а -матрицу называют матрицей перехода. Заметим, что каждый элемент матрицы неотрицателен и что сумма элементов любой из строк равна единице. Из всего этого следует, что — начальный вектор-строка, определенный выше, местоположение осла по прошествии одной минуты описывается вектором-строкой , а после минут — вектором . Другими словами, -я компонента вектора определяет вероятность того, что по истечении минут осел оказался в .