Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Четырехугольники 8 класс геометрия Урок № 1 Многоугольники 1
Содержание
- 1. Четырехугольники 8 класс геометрия Урок № 1 Многоугольники 1
- 2. Цели:Ввести новое понятие «многоугольник».Познакомить с элементами многоугольника.Ввести
- 3. Слайд 3
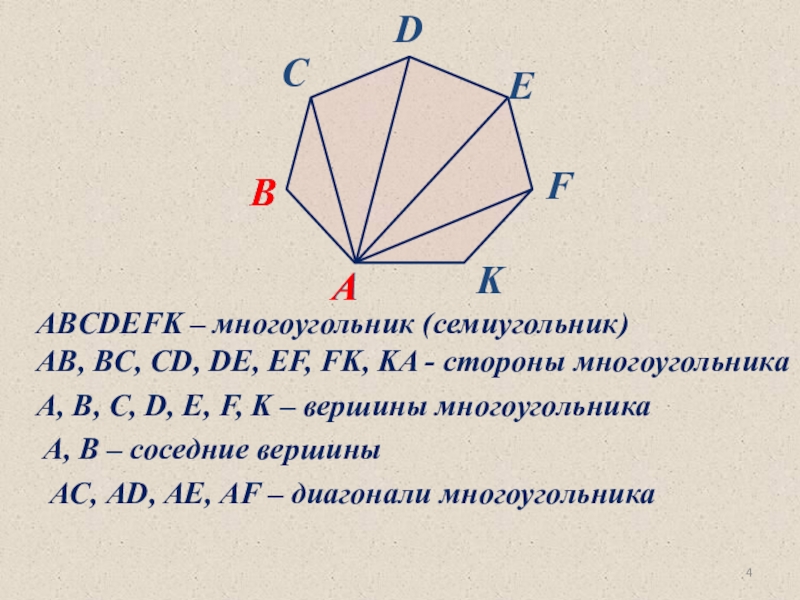
- 4. ABCDEFK – многоугольник (семиугольник) AB, BC, CD,
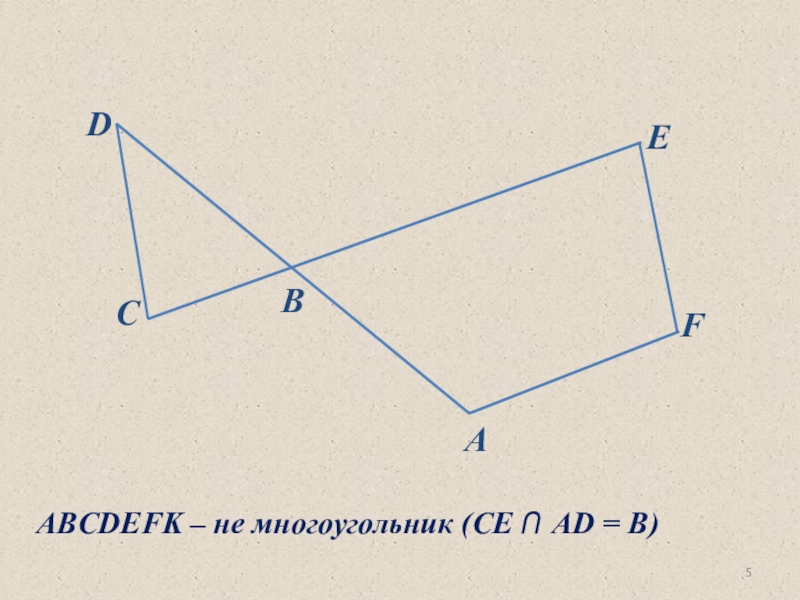
- 5. CDBEFAABCDEFK – не многоугольник (СЕ ⋂ AD = B)
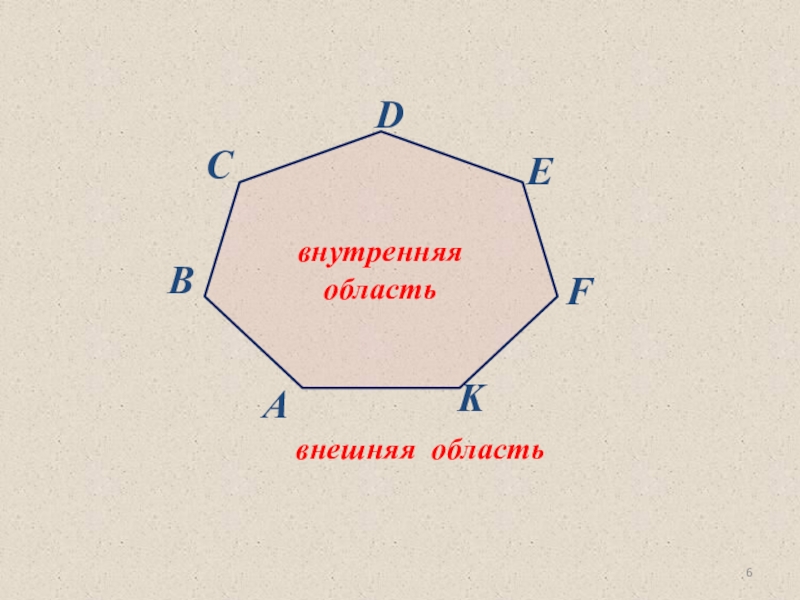
- 6. внутренняя область внешняя область
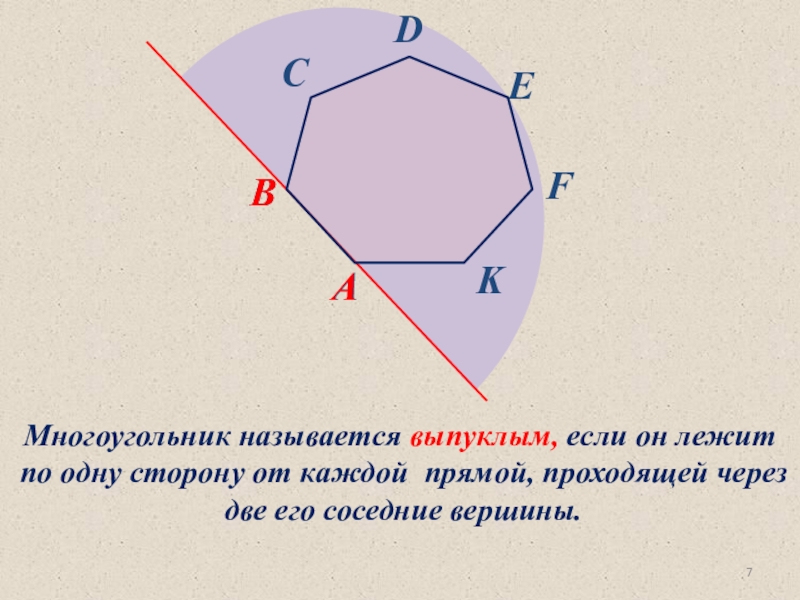
- 7. Многоугольник называется выпуклым, если он лежит по
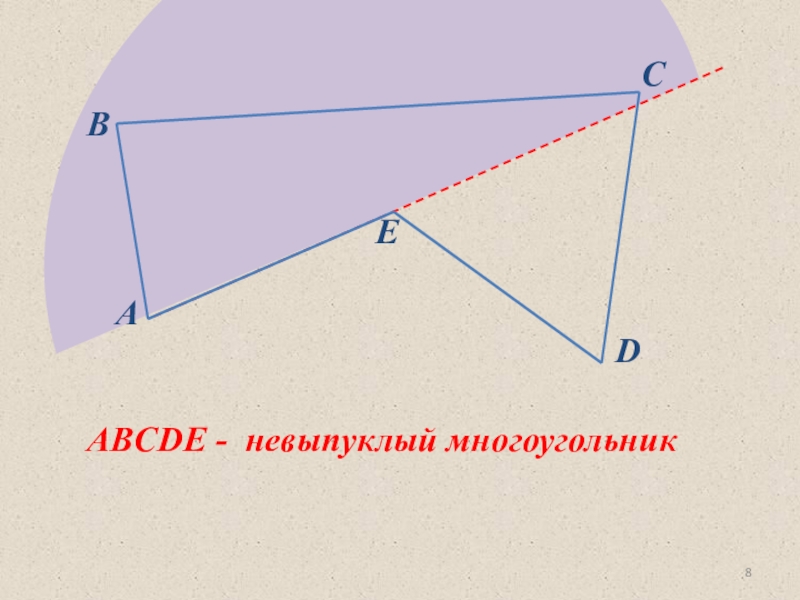
- 8. ABECDABCDE - невыпуклый многоугольник
- 9. ∠AВС, ∠BCD, ∠CDE, ∠DEF, ∠EFK, ∠FKA –
- 10. Слайд 10
- 11. Задача № 365 (в)Сколько сторон имеет многоугольник,
- 12. ЗадачаНайти стороны четырехугольника, если его периметр 66
- 13. 2АВСD – четырехугольник, ∠А = ∠B =∠C
- 14. 3АВСD – четырехугольник, ∠А:∠B:∠C:∠D = 1:2:4:5∠А,∠B, ∠C,
- 15. Ответить на вопросы:Спасибо за внимание!Какая фигура называется
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цели:
Ввести новое понятие «многоугольник».
Познакомить с элементами многоугольника.
Ввести понятия «выпуклый многоугольник»
и «невыпуклый многоугольник».
понятия и формулу нахождения суммы углов выпуклого многоугольника в ходе решения задач.Слайд 4ABCDEFK – многоугольник (семиугольник)
AB, BC, CD, DE, EF, FK,
KA - стороны многоугольника
A, B, C, D, E, F, K
– вершины многоугольника A, B – соседние вершины
AС, AD, AE, AF – диагонали многоугольника
Слайд 7Многоугольник называется выпуклым, если он лежит
по одну сторону от
каждой прямой, проходящей через
две его соседние вершины.
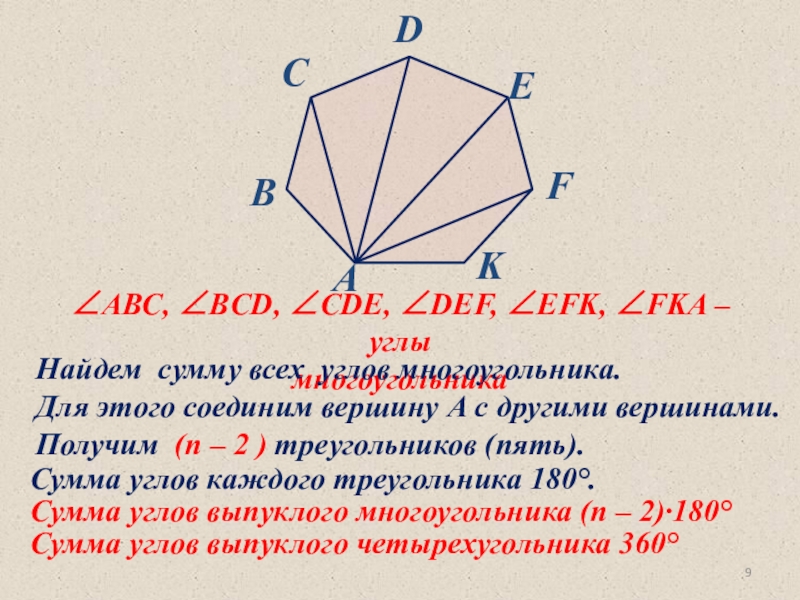
Слайд 9∠AВС, ∠BCD, ∠CDE, ∠DEF, ∠EFK, ∠FKA – углы
многоугольника
Найдем сумму
всех углов многоугольника.
Для этого соединим вершину А с другими
вершинами.Получим (n – 2 ) треугольников (пять).
Сумма углов каждого треугольника 180°.
Сумма углов выпуклого многоугольника (п – 2)·180°
Сумма углов выпуклого четырехугольника 360°
Слайд 11Задача № 365 (в)
Сколько сторон имеет многоугольник, каждый угол
которого равен 120°.
Решение
Так как сумма углов выпуклого многоугольника
(п
– 2) · 180°.То следовательно (п – 2) · 180° = 120° · п
Обозначим п – количество сторон многоугольника.
180° · п - 360° = 120° · п
60° · п = 360°
п = 360° : 60°
п = 6
Ответ: 6 сторон.
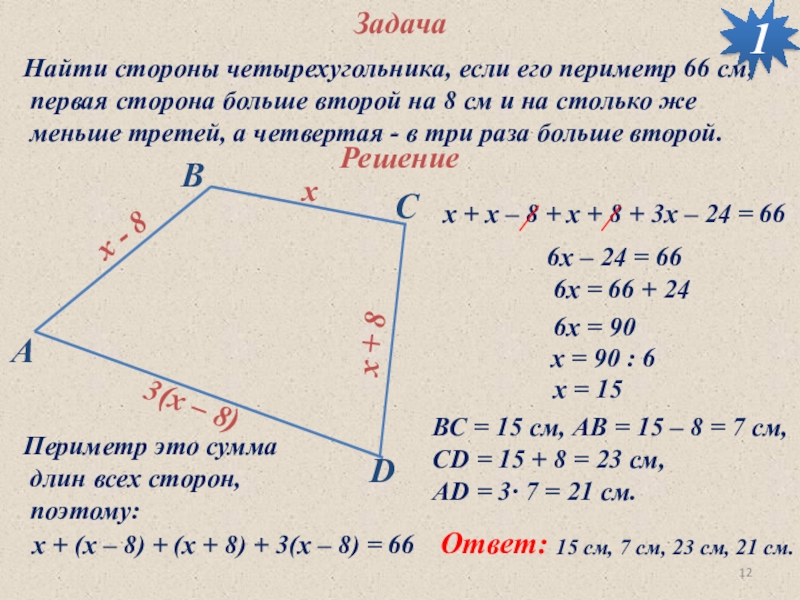
Слайд 12Задача
Найти стороны четырехугольника, если его периметр 66 см,
первая сторона
больше второй на 8 см и на столько же
меньше третей, а четвертая - в три раза больше второй.1
Решение
x
x - 8
x + 8
3(x – 8)
Периметр это сумма
длин всех сторон,
поэтому:
х + (x – 8) + (х + 8) + 3(х – 8) = 66
х + x – 8 + х + 8 + 3х – 24 = 66
6х – 24 = 66
6х = 66 + 24
6х = 90
х = 90 : 6
х = 15
ВС = 15 см, AB = 15 – 8 = 7 см,
CD = 15 + 8 = 23 cм,
AD = 3· 7 = 21 см.
Ответ:
15 см, 7 см, 23 cм, 21 см.
Слайд 132
АВСD – четырехугольник, ∠А = ∠B =∠C =∠D
∠А -?
Решение
По формуле о сумме углов
многоугольника имеем:
(п – 2)·180°
= (4 – 2)·180° = 360°По условию ∠А = ∠B =∠C =∠D,
следовательно ∠А = 360° : 4 = 90°
Ответ: 90°
Слайд 143
АВСD – четырехугольник,
∠А:∠B:∠C:∠D = 1:2:4:5
∠А,∠B, ∠C, ∠D - ?
Решение
∠А + ∠B + ∠C + ∠D = 360°
Пусть
∠А = хтогда ∠B = 2х, ∠C = 4х, ∠D = 5х
х + 2х + 4х + 5х = 360°
12х = 360°
х = 360° : 12
х = 30°
∠А = 30°, ∠B = 2х = 60°, ∠C = 4х = 120°, ∠D = 5х = 150°
Ответ: 30°, 60°, 120°, 150°
Слайд 15Ответить на вопросы:
Спасибо за внимание!
Какая фигура называется многоугольником?
Что такое вершина,
стороны, углы, диагонали
и периметр многоугольника?
Какой многоугольник называется выпуклым?
Формула вычисления
суммы углов выпуклого многоугольника.
Чему равна сумма углов выпуклого
четырехугольника?