Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Численные методы решения нелинейных уравнений с одним неизвестным
Содержание
- 1. Численные методы решения нелинейных уравнений с одним неизвестным
- 2. Определение нелинейного уравненияВ общем виде нелинейное уравнение
- 3. а) Алгебраическими называются уравнения Y(x)=0, которые могут
- 4. Примеры трансцендентных уравнений: Любимов Е.Б.
- 5. Решением или корнем уравнения Y(x)=0 (1) называется значения
- 6. Методы решения нелинейных уравненийАналитические (прямые, точные) методы
- 7. Аналитические решения могут быть получены для алгебраических
- 8. Алгебраические уравнения, имеющие аналитические решения:линейные уравнения: a*x+b=0
- 9. Итерационные методы – методы последовательных приближений, реализуют
- 10. Общий подход к решению нелинейных
- 11. Признак нахождения корня в интервале [a; b]Y(a)*Y(b)
- 12. ε-εЛюбимов Е.Б.
- 13. График исследуемой функцииЛюбимов Е.Б.
- 14. График функции с точкой разрыва Любимов Е.Б.
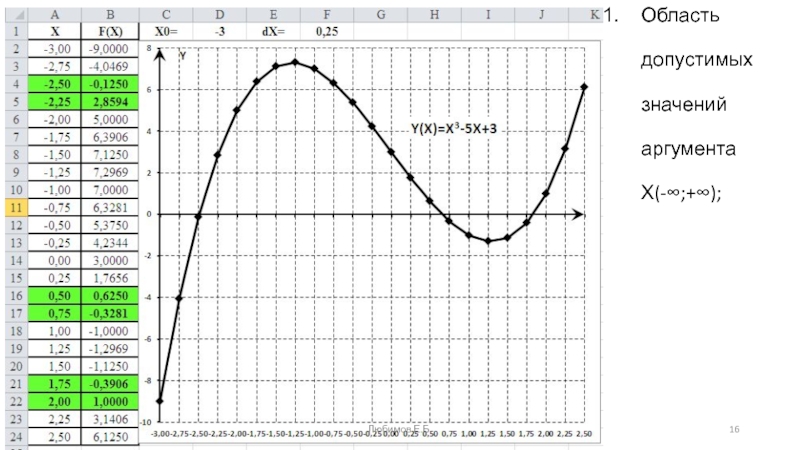
- 15. 1a) интервал допустимых изменений аргумента x
- 16. Область допустимых значений аргумента Х(-∞;+∞);Любимов Е.Б.
- 17. 1-й корень Є(-2,5; -2,25);Y(-2,5) = -0,1250; Y(-2,25)
- 18. Начальный интервал нахождения корня [a0;b0]: Y(a0)*Y(b0)
- 19. Реализация метода дихотомии в среде MS ExcelУточнение
- 20. Формулы изменения граничных значений аi и bi
- 21. Заголовок, первая и вторая строки таблицы (столбцы от F до J)d - длина интервала неопределённости(d
- 22. Результаты решения уравнения методом дихотомииЛюбимов Е.Б.
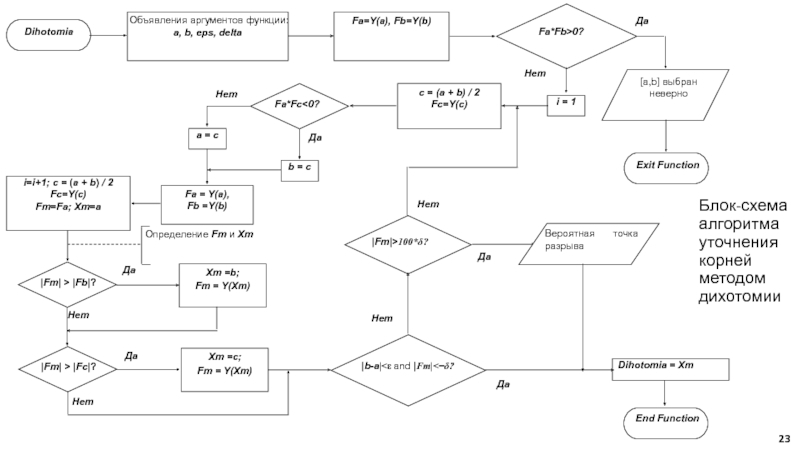
- 23. Блок-схема алгоритма уточнения корней методом дихотомии Любимов Е.Б.
- 24. ' Текст функции Dihotomia с отладочными выводамиPublic
- 25. i = 1 ' вход в
- 26. Fm = Fa: Xm = a
- 27. Результаты выполнения табличного решения и решения, полученного при обращении к функции Dihotomia()Любимов Е.Б.
- 28. Метод хордУравнение прямой, проходящей через точки Y(a)
- 29. Завершение процесса уточнения корняЛюбимов Е.Б.
- 30. Любимов Е.Б.
- 31. Реализация метода хорд в среде MS ExcelУточнение
- 32. Любимов Е.Б.Формулы реализации метода хорд в среде MS Excel столбцы от E до J
- 33. Уточнение значения наименьшего из корней уравнения F(x)=X3-5X+3
- 34. Уточнение значения второго корня уравнения F(x)=X3-5X+3 методом
- 35. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Определение нелинейного уравнения
В общем виде нелинейное уравнение с одним неизвестным
можно записать в виде
Y(x) = 0,
(1)где х - действительное число,
а Y(x) - нелинейная функция.
Любимов Е.Б.
Слайд 3а) Алгебраическими называются уравнения Y(x)=0, которые могут быть представлены в
форме канонического полинома:
Типы нелинейных уравнений:
где x – аргумент функции Y(x),
a0, a1, a2, …, an – коэффициенты уравнения .
б) Трансцендентными ("конечными") называются уравнения неприводимые к виду алгебраических, в которых функция Y(x) содержит тригонометрические, показательные, логарифмические и другие функции, не являющиеся алгебраическими.
Любимов Е.Б.
Слайд 5Решением или корнем уравнения
Y(x)=0 (1)
называется значения аргумента х, обращающее
равенство (1) в тождество.
Любимов Е.Б.
Слайд 6Методы решения нелинейных уравнений
Аналитические (прямые, точные) методы решения:
Методы, позволяющие записать
решение уравнения в виде некоторого соотношения (формулы).
Значения аналитических решений
вычисляются за конечное число арифметических операций.2. Итерационные методы позволяют получить приближенные значения корней с любой заданной точностью.
Число операций, необходимых для этого, не может быть определено заранее.
Любимов Е.Б.
Слайд 7Аналитические решения могут быть получены для алгебраических уравнений не выше
четвертой степени и для некоторых видов трансцендентных уравнений
Алгебраические уравнения
(2)
Любимов Е.Б.
Слайд 8
Алгебраические уравнения, имеющие аналитические решения:
линейные уравнения: a*x+b=0
(или a0 + a1*x =
0);квадратные уравнения: a*x2+b*x + c=0 (или a0 + a1*x + a2*x2= 0);
кубичные уравнения: a0 + a1*x + a2*x2 + a3*x3 = 0 ;
уравнения четвертой степени: a0 +a1x + a2*x2 + a3*x3 + a4*x4 = 0.
Любимов Е.Б.
Слайд 9Итерационные методы – методы последовательных приближений, реализуют алгоритмы, обеспечивающие нахождение
решения за несколько последовательно выполняемых шагов - итераций.
Число шагов
итерации заранее не известно. На каждом шаге итеративного процесса точность решения увеличивается.
Любимов Е.Б.
Слайд 10
Общий подход к решению нелинейных уравнений
Решение нелинейных уравнений численными методами
обычно осуществляется в два этапа:
1 этап –
отделение (локализация) корней :анализ функции - определение интервала(ов) допустимых изменений значений аргумента X функции (X0, Xk);
выделение на определённом(ых) в анализе интервале(ах) изменения аргумента [X0, Xk] подынтервалов [xi,xj], содержащих по одному корню.
2 этап - уточнение корня на выбранном промежутке [xi,xj], содержащем один корень.
Любимов Е.Б.
Слайд 11
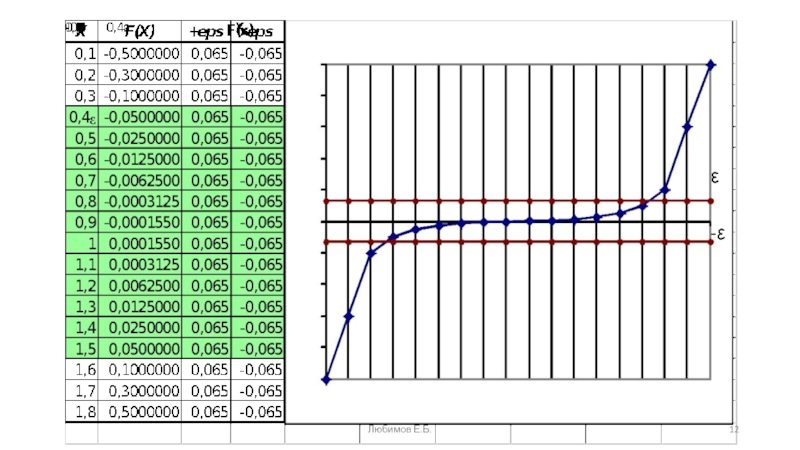
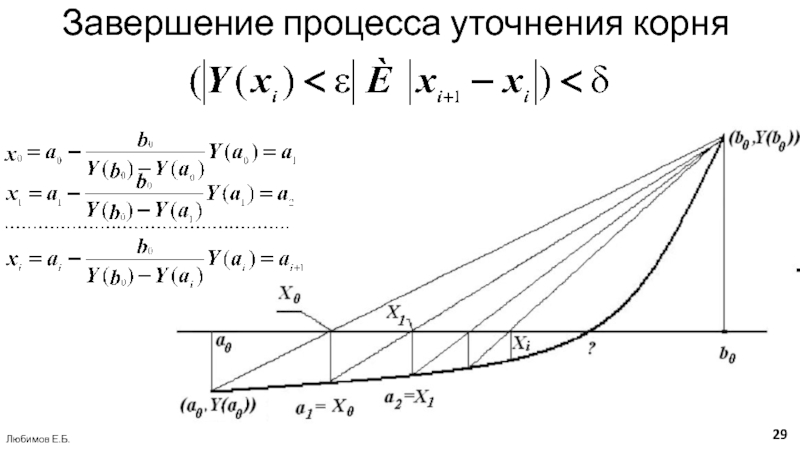
Признак нахождения корня в интервале [a; b]
Y(a)*Y(b)
считается найденным, если
| Y(xi) | ≤ ε ,
(4)либо, если
|(xi+1-xi)| ≤ δ, (5)
где ε и δ - некоторые положительные вещественные константы.
Любимов Е.Б.
Слайд 15
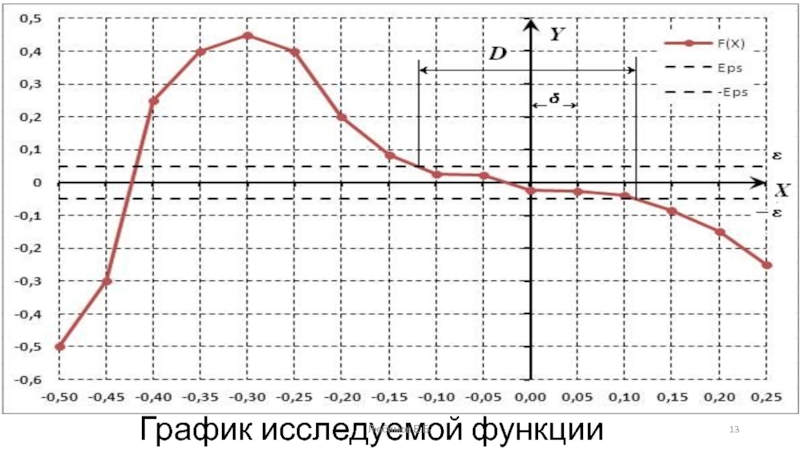
1a) интервал допустимых изменений аргумента x Є [-∞; +∞];
1б) В интервале изменения функции Y(x) могут находиться один или
три вещественных корня.Пример. Выполнить предварительный анализ функции
Любимов Е.Б.
Слайд 171-й корень Є(-2,5; -2,25);
Y(-2,5) = -0,1250; Y(-2,25) = 2,8594
2-й корень
Є(0,5;0,75);
Y(0,5) = 0,6250; Y(0,75) = -0,3281
3-й корень Є(1,75; 2,00);
Y(1,75) =
-0,3906; Y(2,00) =1,0000Любимов Е.Б.
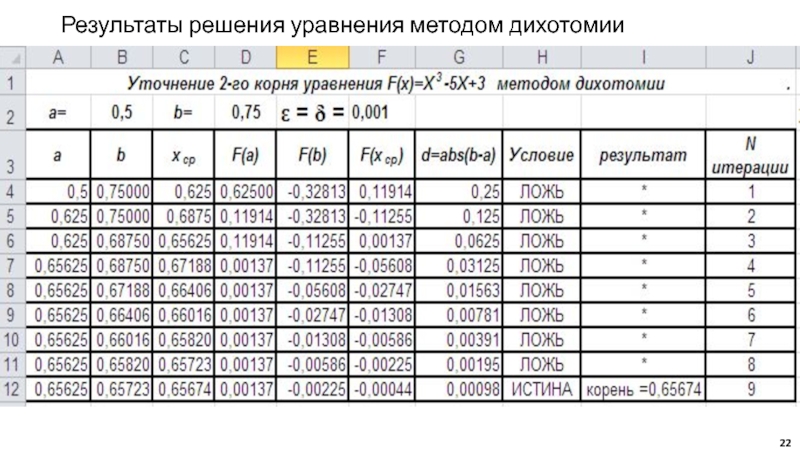
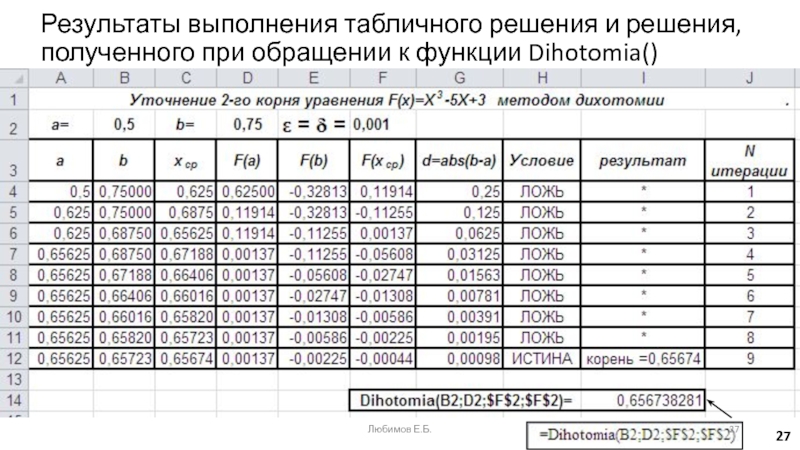
Слайд 19Реализация метода дихотомии в среде MS Excel
Уточнение 2-го корня уравнения
F(x)=X3-5X+3 методом дихотомии заголовок таблицы: a0=0,5; b0= 0,75; ε = δ
= 0,001Формирование заголовка и первой строки таблицы (столбцы от А до F)
Ссылки на ячейки со значениями параметров а0 и b0
Формулы для вычисления значений Хср, F(a), F(b) и F(Xcp)
Любимов Е.Б.
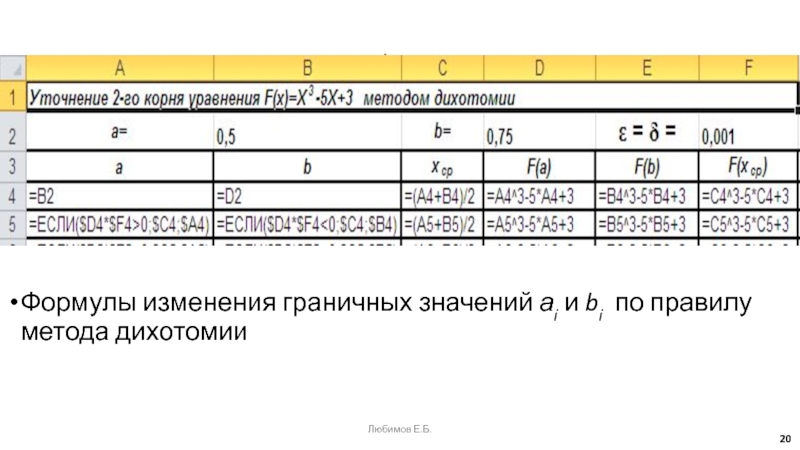
Слайд 20Формулы изменения граничных значений аi и bi по правилу метода
дихотомии
Заголовок, первая и вторая строки таблицы (столбцы от А до
F) Любимов Е.Б.
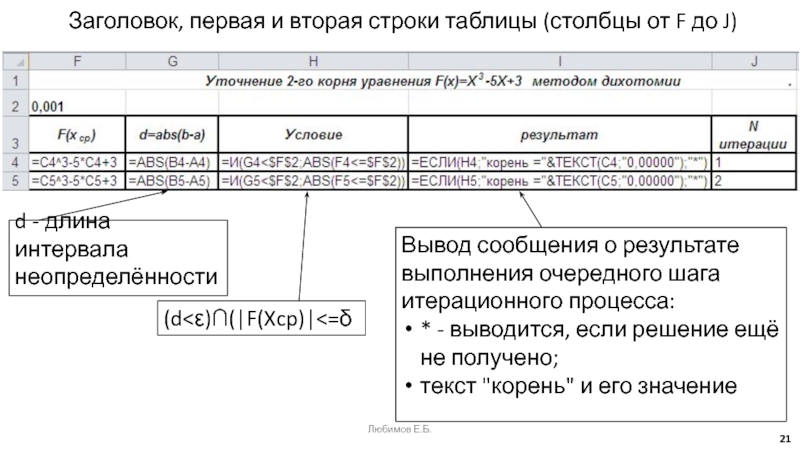
Слайд 21 Заголовок, первая и вторая строки таблицы (столбцы от F
до J)
d - длина интервала
неопределённости
(d
очередного шага итерационного процесса:* - выводится, если решение ещё не получено;
текст "корень" и его значение
Любимов Е.Б.
Слайд 24' Текст функции Dihotomia с отладочными выводами
Public Function Dihotomia(a As
Double, b As Double, _
eps As Double, delta As Double) As DoubleDim i As Integer ' счётчик числа итераций
Dim c As Double, Fa As Double, Fb As Double, Fc As Double
Dim Fm As Double, Xm As Double
Fa = Y(a): Fb = Y(b)
If Fa * Fb > 0 Then
MsgBox ("Начальный выбор интервала [a,b] сделан _ неверно")
Exit Function
End If
Любимов Е.Б.
Слайд 25 i = 1 ' вход в цикл определения корня
Do ' While ((Abs(b - a) > eps) And
(Abs(Fm) > delta))c = (a + b) / 2: Fc = Y(c):
' MsgBox "i= " & i & " c= " & c & "; Fc= " & Fc
' выполнение шага метода дихотомии
If Fa * Fc < 0 Then b = c Else a = c
' вычисление новых значений функции на границах интервала
Fa = Y(a): Fb = Y(b):
' MsgBox "i= " & i & " | a=" & a & " ; Fa=" & Fa & _
' " | b=" & b & " ; Fb=" & Fb
i = i + 1
' выбор точки с наименьшим значением F(X)
c = (a + b) / 2: Fc = Y(c):
' MsgBox "i= " & i & " | a=" & a & " ; Fa=" & Fa & " | b=" & b _
& " ; Fb=" & Fb & " | c=" & c & " ; Fc=" & Fc
Любимов Е.Б.
Слайд 26 Fm = Fa: Xm = a ' определение точки
Xm с наименьшим Y(Xm)
If (Abs(Fm) > Abs(Fb)) Then
Xm = b: Fm = Y(Xm)End If
If (Abs(Fm) > Abs(Fc)) Then
Xm = c: Fm = Y(Xm)
End If
If ((Abs(b - a) < eps) And (Abs(Fm) > delta * 100)) Then GoTo E
' MsgBox "i= " & i & " | корень Xm=" & Xm & " ; F(Хm) =" & Fm
Loop Until ((Abs(b - a) < eps) And (Abs(Fm) <= delta)): GoTo E1
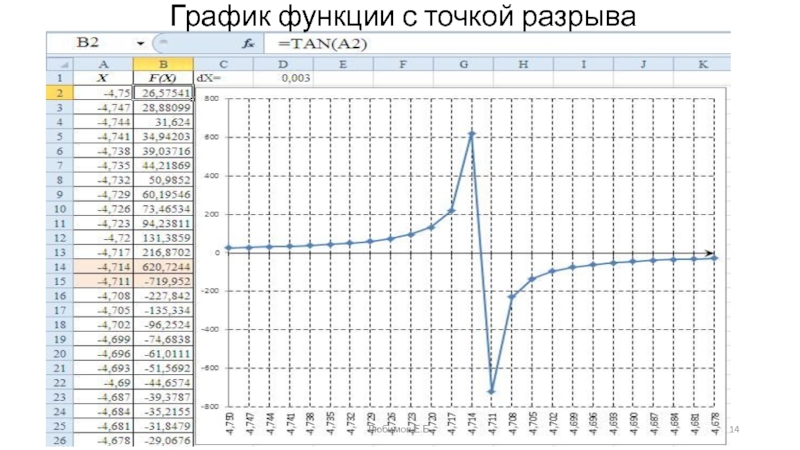
E: MsgBox " Вероятная точка разрыва "
E1: 'MsgBox "число итераций i= " & i & " | Xm=" & Xm & _
" | Fm= " & Fm
Dihotomia = Xm
End Function
Любимов Е.Б.
Слайд 27Результаты выполнения табличного решения и решения, полученного при обращении к
функции Dihotomia()
Любимов Е.Б.
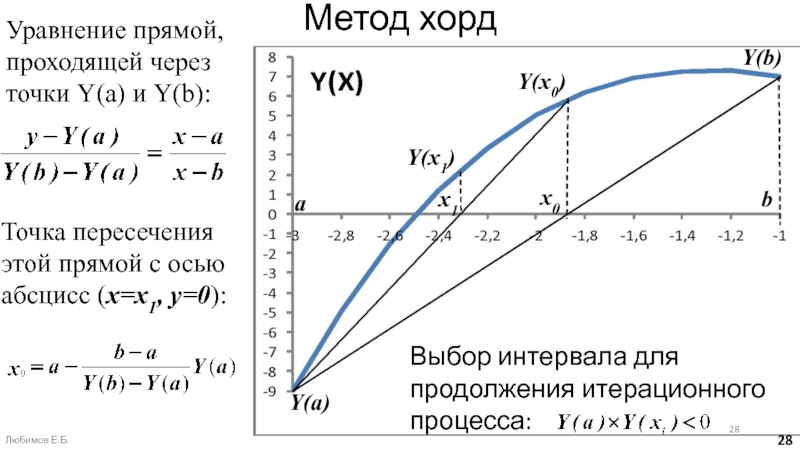
Слайд 28Метод хорд
Уравнение прямой, проходящей через точки Y(a) и Y(b):
Точка пересечения
этой прямой с осью абсцисс (х=х1, y=0):
Выбор интервала для продолжения
итерационного процесса:Y(a)
Любимов Е.Б.
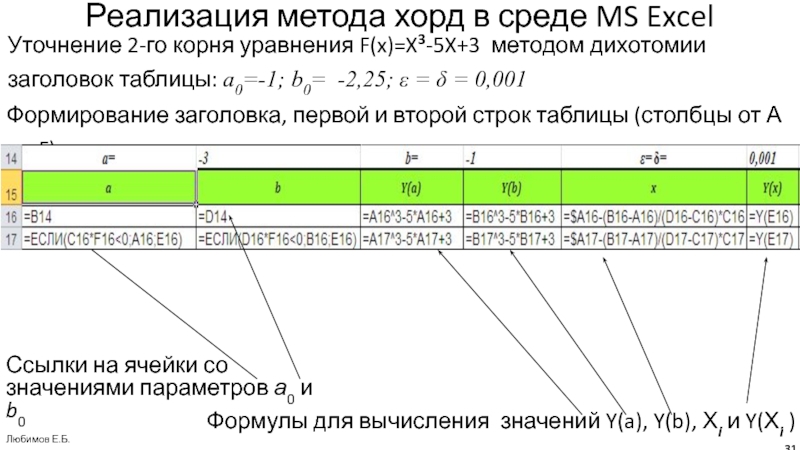
Слайд 31Реализация метода хорд в среде MS Excel
Уточнение 2-го корня уравнения
F(x)=X3-5X+3 методом дихотомии заголовок таблицы: a0=-1; b0= -2,25; ε = δ
= 0,001Формирование заголовка, первой и второй строк таблицы (столбцы от А до F)
Ссылки на ячейки со значениями параметров а0 и b0
Формулы для вычисления значений Y(a), Y(b), Хi и Y(Хi )
Любимов Е.Б.
Любимов Е.Б.
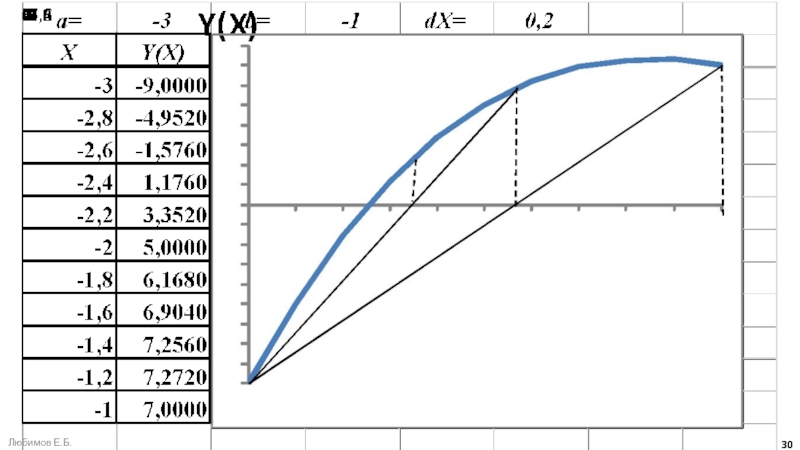
Слайд 33Уточнение значения наименьшего из корней уравнения F(x)=X3-5X+3 методом хорд при
выборе начального интервала неопределённости [-3; -1]
Любимов Е.Б.
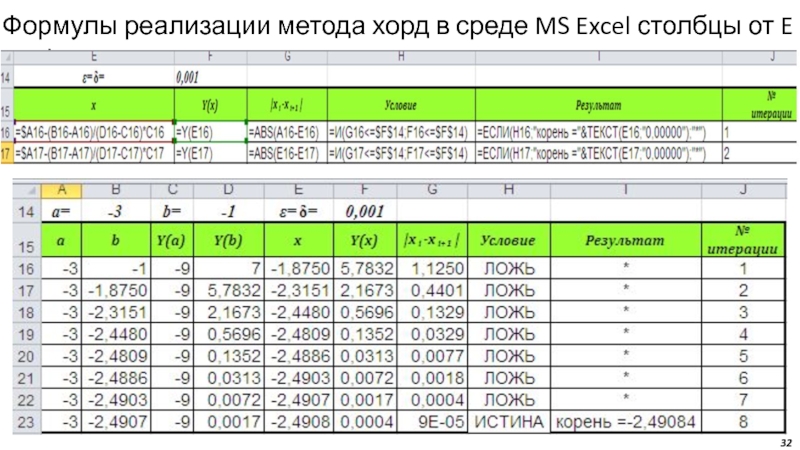
Слайд 34Уточнение значения второго корня уравнения F(x)=X3-5X+3 методом хорд при выборе
начального интервала неопределённости [0,5; 0,75] (для сравнения с результатами на слайде
27)Любимов Е.Б.



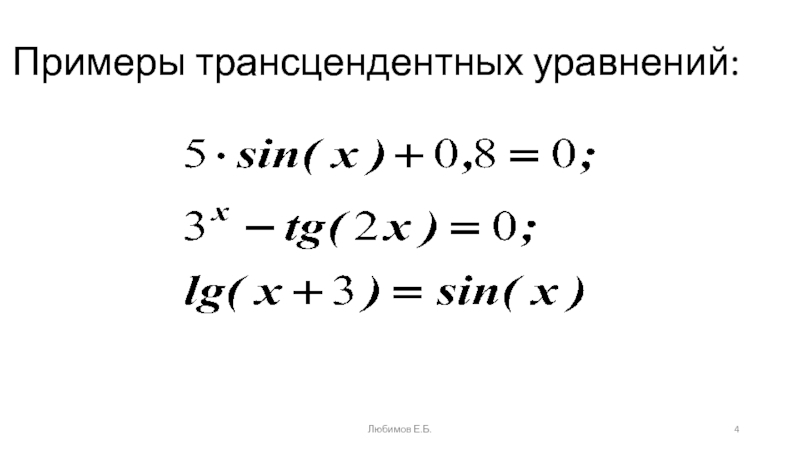






![Численные методы решения нелинейных уравнений с одним неизвестным Признак нахождения корня в интервале [a; b]Y(a)*Y(b) Признак нахождения корня в интервале [a; b]Y(a)*Y(b)](/img/thumbs/fa84746cf0ea7c1f152cf66ac2c322af-800x.jpg)
![Численные методы решения нелинейных уравнений с одним неизвестным 1a) интервал допустимых изменений аргумента x Є [-∞; +∞]; 1б) 1a) интервал допустимых изменений аргумента x Є [-∞; +∞]; 1б) В интервале изменения функции Y(x) могут](/img/thumbs/9a37d5151641a8e888bc26d3d97877a0-800x.jpg)

![Численные методы решения нелинейных уравнений с одним неизвестным Начальный интервал нахождения корня [a0;b0]: Y(a0)*Y(b0) Начальный интервал нахождения корня [a0;b0]: Y(a0)*Y(b0)](/img/thumbs/92878417a447fd2dcbbace18d53c52cd-800x.jpg)




![Численные методы решения нелинейных уравнений с одним неизвестным Уточнение значения наименьшего из корней уравнения F(x)=X3-5X+3 методом хорд при выборе Уточнение значения наименьшего из корней уравнения F(x)=X3-5X+3 методом хорд при выборе начального интервала неопределённости [-3; -1]Любимов Е.Б.](/img/thumbs/151a016313c6076d6d6073b3c87454f0-800x.jpg)
![Численные методы решения нелинейных уравнений с одним неизвестным Уточнение значения второго корня уравнения F(x)=X3-5X+3 методом хорд при выборе начального Уточнение значения второго корня уравнения F(x)=X3-5X+3 методом хорд при выборе начального интервала неопределённости [0,5; 0,75] (для сравнения](/img/thumbs/176235e4bb96fcae45379019afb01d28-800x.jpg)



















