Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовая окружность на координатной плоскости
Содержание
- 1. Числовая окружность на координатной плоскости
- 2. Числовая окружность на координатной плоскости.Что будем изучать:
- 3. Определение.Числовая окружность на координатной плоскости.Расположим числовую окружность
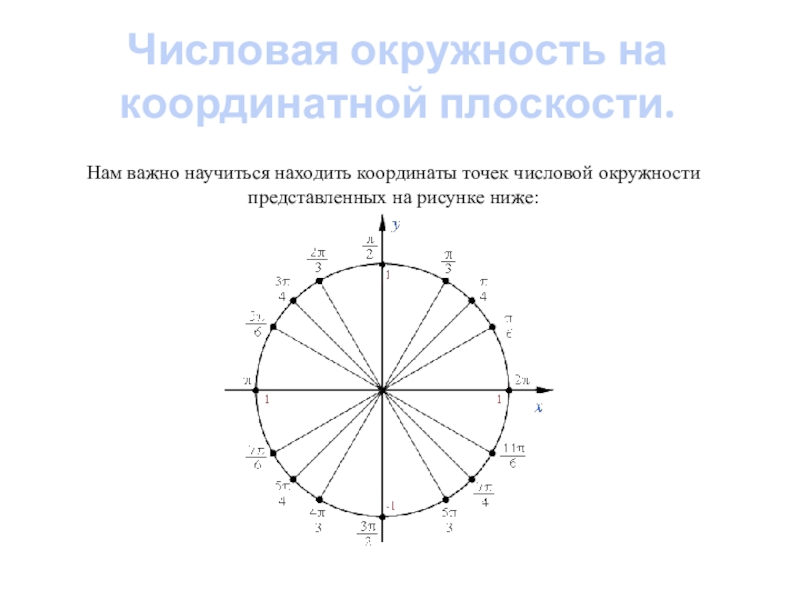
- 4. Числовая окружность на координатной плоскости.Нам важно научиться находить координаты точек числовой окружности представленных на рисунке ниже:
- 5. Числовая окружность на координатной плоскости.Найдем координату точки
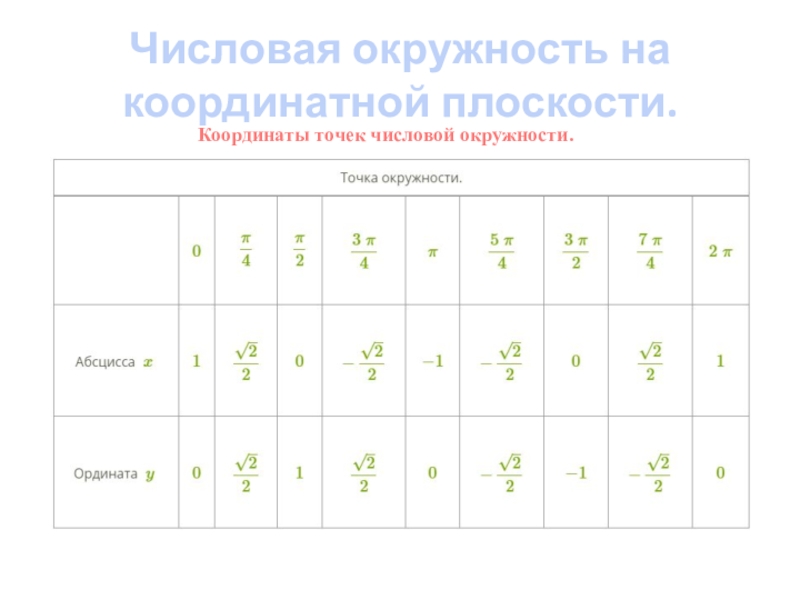
- 6. Координаты точек числовой окружности.Числовая окружность на координатной плоскости.
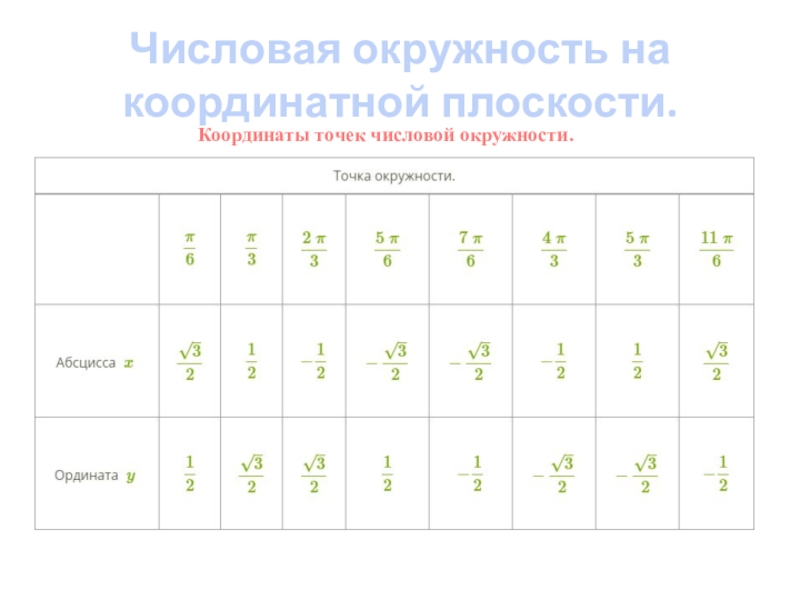
- 7. Координаты точек числовой окружности.Числовая окружность на координатной плоскости.
- 8. ПримерНайти координату точки числовой окружности: Р(45π/4)Решение:Т.к. числам
- 9. ПримерНайти координату точки числовой окружности: Р(-37π/3)Решение:Т.к. числам
- 10. Найти на числовой окружности точки с ординатой
- 11. ПримерНайти на числовой окружности точки с абсциссой
- 12. Задачи для самостоятельного решения.1) Найти координату точки
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Числовая окружность на координатной плоскости.
Что будем изучать:
Определение.
Важные координаты числовой
окружности.
Слайд 3Определение.
Числовая окружность на координатной плоскости.
Расположим числовую окружность в координатной плоскости
так, чтобы центр окружности совместился с началом координат, а её
радиус принимаем за единичный отрезок. Начальная точка числовой окружности A совмещена с точкой (1;0).Каждая точка числовой окружности имеет в координатной плоскости свои координаты х и у, причем:
x > 0, у > 0 в первой четверти;
х < 0, у > 0 во второй четверти;
х < 0, у < 0 в третьей четверти;
х > 0, у < 0 в четвертой четверти.
Для любой точки М(х; у) числовой окружности выполняются неравенства -1 < x < 1; -1 < у < 1.
Запомните!
уравнение числовой окружности:
Слайд 4Числовая окружность на координатной плоскости.
Нам важно научиться находить координаты точек
числовой окружности представленных на рисунке ниже:
Слайд 5Числовая окружность на координатной плоскости.
Найдем координату точки π/4:
Точка М(π/4)
— середина первой четверти. Опустим из точки М перпендикуляр МР
на прямую ОА и рассмотрим треугольник OMP.Так как дуга АМ составляет половину дуги АВ, то ∡MOP=45°Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M абсцисса и ордината равны: x = y
Так как координаты точки M(х;y) удовлетворяют уравнению числовой окружности, то для их нахождения нужно решить систему уравнений:
Решив данную систему получаем:
Получили, что координаты точки M, соответствующей числу π/4 будут
Аналогичным образом рассчитываются координаты точек представленных на предыдущем слайде.
Слайд 8Пример
Найти координату точки числовой окружности: Р(45π/4)
Решение:
Т.к. числам t и t+2π•k
(k-целое число) соответствует одна и тоже точка числовой окружности то:
45π/4
= (10 + 5/4) • π = 10π +5π/4 = 5π/4 + 2π•5Значит, числу 45π/4 соответствует та же точка числовой окружности, что и числу 5π/4. Посмотрев значение точки 5π/4 в таблице получаем:
Числовая окружность на координатной плоскости.
Слайд 9Пример
Найти координату точки числовой окружности: Р(-37π/3)
Решение:
Т.к. числам t и t+2π•k
(k-целое число) соответствует одна и тоже точка числовой окружности то:
-37π/3
= -(12 + 1/3) • π = -12π –π/3 = -π/3 + 2π•(-6)Значит, числу -37π/3 соответствует та же точка числовой окружности, что и числу –π/3, а числу –π/3 соответствует та же точка что и 5π/3. Посмотрев значение точки 5π/3 в таблице получаем:
Числовая окружность на координатной плоскости.
Слайд 10Найти на числовой окружности точки с ординатой у = 1/2
и записать, каким числам t они соответствуют.
Пример
Прямая у = 1/2
пересекает числовую окружность в точках М и Р. Точка М соответствует числу π/6 (из данных таблицы) значит, и любому числу вида π/6 +2π •k . Точка Р соответствует числу 5π/6, а значит, и любому числу вида 5π/6 +2 π •k Получили, как часто говорят в таких случаях, две серии значений: π/6 +2 π •k и 5π/6 +2 π •k
Ответ : t= π/6 +2 π •k и t= 5π/6 +2 π •k
Числовая окружность на координатной плоскости.
Слайд 11Пример
Найти на числовой окружности точки с абсциссой x≥
и записать, каким числам t они соответствуют.
Прямая x = 1/2
пересекает числовую окружность в точках М и Р. Неравенству x ≥ соответствуют точки дуги РМ.Точка М соответствует числу 3π/4 (из данных таблицы) значит, и любому числу вида -3π/4 +2π•k . Точка Р соответствует числу -3π/4, а значит, и любому числу вида –
-3π/4 +2 π •k
Тогда получим -3π/4 +2 π •k ≤t≤3π/4 +2 π •k
Ответ : -3π/4 +2 π •k ≤t≤3π/4 +2 π •k
Числовая окружность на координатной плоскости.
Слайд 12Задачи для самостоятельного решения.
1) Найти координату точки числовой окружности: Р(61π/6)?
2)
Найти координату точки числовой окружности: Р(-52π/3)
3) Найти на числовой
окружности точки с ординатой у = -1/2 и записать, каким числам t они соответствуют.4) Найти на числовой окружности точки с ординатой у ≥ -1/2 и записать, каким числам t они соответствуют.
5)Найти на числовой окружности точки с абсциссой x≥
и записать, каким числам t они соответствуют.
Числовая окружность на координатной плоскости.