Числовые характеристики непрерывной сл. в.Нормальное распределение без кривой Гаусса

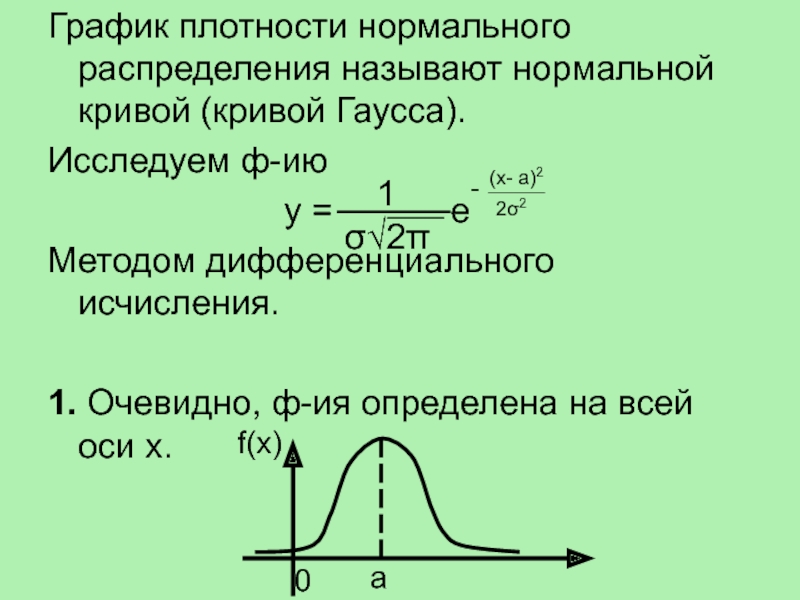
ожиданием непрерывной случайной величины Х, возможные значения которой xЄ[а; b],

называют определенный интеграл:
M (X) = ∫ x f(x) dx.
Если возможные значения принадлежат всей оси Ох, то M (X) = ∫ x f(x) dx,
х – М (Х) – есть отклонение величины Х.
Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл ∫ |x| f(x) dx

b

a

-∞

∞

∞

-∞

отклонения.
Если возможные значения Х Є [а; b], то
D(X) = ∫

[x – M(X)]2 f(x)dx.
Если х Є [-∞; ∞], то
D(X) = ∫ [x – M(X)]2 f(x)dx.
♦ Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для дискретных величин, равенством:
σ (Х) = √ D (X) .

b

а

∞

-∞

дискретных величин сохраняются и для непрерывных величин.
Замечание 2. Легко получить

для вычисления дисперсии более удобные формулы:
D(X) = ∫ х2 f(x)dx - [M(X)]2;

D(X) = ∫ х2 f(x)dx - [M(X)]2.

b

а

∞

-∞

ф-ей распределения:

0 при х ≤ 0
F(x) = х при 0 < х ≤ 1
1 при х > 1.

Решение. Найдем плотность распределения:

0 при х < 0
f(х) = F'(x) = 1 при 0 < х < 1
0 при х > 1.

= 1/2.

Дисперсия:

D(X) = ∫ х2 ·1· dx - [1/2]2

= х3/3 - 1/4 = 1/12.

0

1

1

0

1

0

0

1

определяется плотностью
f(x) = е -(х- а)2/2σ2.

Норм. распределение опред-ся 2-мя параметрами а и σ.
Вероятностный смысл этих параметров таков:
а – есть математическое ожидание, а
σ – среднее квадратичное отклонение формального распределения.

1

σ √2π

(σ>0).
Нормированным называют норм. распр-ие с параметрами а=0 и σ=1. Напр.,

если
Х – нормальная величина с параметрами а и σ, то
U = (Х - а)/σ – нормированная нормальная величина, причем М(U)=0, σ(U)=1.
Плотность нормированного распределения
φ(x) = е-х2/2.
Эта ф-ция фигурирует в локальной теореме Лапласа и затабулирована.

1

√2π

для приближенных вычислений используют локальную теорему Лапласа:
«Вероятность того, что в

n независимых испытаниях, в каждом из которых вероятность появления события А равна р, событие А наступит ровно k раз, приближенно равна
Рn(k) φ(x), где φ(x)= е-х2/2,

1

√npq

k-np

√2π

Х=

k-np

√npq

таблица для положительных х приводится в приложениях учебных пособий. Т.к.

ф-ия φ(x) четная, то для отрицательных значений х можно воспользоваться формулой φ(-x) = φ(x).

каждом из которых вероятность появления события А равна р, событие

А наступит не менее k1 раз и не более k2 раз, приближенно равна
Рn(k1; k2) ≈ Ф(х'') - Ф(х'), где
Ф(х) = ∫е-Z2/2·dz – ф-ия Лапласа,

х'= , х''= , k2>k1.

1

√2π

k1-np

√npq

k2-np

√npq

Ф(-х) = Ф(х),
для х>5 Ф(х)=0,5.

у = е
Методом дифференциального исчисления.

1. Очевидно, ф-ия определена на всей оси х.

1

σ√2π

(х- а)2

2σ2

-

а

0

f(x)

Lim y = 0, т.е. у=0 – ось Ох служит

горизонтальной асимптотой графика.
4. Исследуем ф-ию на экстремум.
у' = - е .

Легко видеть, что у'=0 при х=а, у'>0 при ха. Согласно достаточному условию экстремума при х=а ф-ия имеет максимум:
уmax= .

-

(х- а)2

2σ2

σ3√2π

х - а

1

√2π

х→±∞

т.е. график симметричен относительно прямой х=а.

6. Исследуем ф-ию на точки

перегиба (где график меняет характер выпуклости)
у'' = - е-(х-а)2/2σ2·[1 - ].

1

σ3√2π

(х-а)2

σ2

производная меняет знак (в обеих этих точках значение ф-ии равно

Таким

образом, точки графика
(а – σ; ) и (а + σ; )

являются точками перегиба.

1

σ√2πe

σ√2πe

1

1

σ√2πe

f(x-a) получается параллельным переносом графика f(x) на а единиц масштаба

вправо, если а>0.
Отсюда следует, что изменение величины параметра а (матем. ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если «а» возрастает, и влево, если «а» убывает. Иное дело с σ. Максимум нормальной кривой распределения равен .

1

σ√2π

кривая становиться более пологой, т.е. сжимается к оси Ох; при

убывании σ нормальная кривая становиться более «островершинной» и растягивается в положительном направлении оси Оу.
Важно заметить, что при любых значениях а и σ площадь, ограниченная нормальной кривой и осью х остается равной 1.
(В частности при σ→0 получаем одно из определений дельта-функции Дирака).

называют нормированной).
f(x)



х
0
σ1
σ2
σ3

= ∫f(x)dx – вероятность
того, что случайная величина Х примет значения

из (α; β).
Пусть Х – нормальная величина. Тогда
P (αЧтобы пользоваться готовыми таблицами, преобразуем эту формулу:
P (α

β

α

1

σ√2π

(х-а)2

β

α

2σ2

β-α

α-а

σ

σ

нормально распределенной случайной величины Х по абсолютной величине меньше заданного

положительного числа δ, т.е. требуется найти вероятность осуществления неравенства |Х-а|<δ.

P (|Х-а|<δ) = 2Ф( ).

δ

σ

чем меньше σ (рассеяние нормальной случайной величины вокруг ее мат.

ожидания), тем больше вероятность принять значение, принадлежащее интервалу (-δ; δ).

δ

σ

) положим δ=σ·t, тогда
P (|Х-а|

= 3 и,
следовательно, σ t = 3σ , то
P (|Х-а|<3σ) = 2Ф(3) = 2·0,49865 = 0,9973 ,
т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

δ

σ

среднее квадратичное отклонение, очень мала, а именно равна 0,0027. Т.е.

в 0,27% случаев так может произойти. Такие события можно считать практически невозможными.
Правило 3-х сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

3-х сигм, то есть основание предполагать, что изучаемая величина распределена

нормально.
В противном случае она не распределена нормально.