Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Числовые характеристики одномерных и двумерных случайных величин
Содержание
- 1. Числовые характеристики одномерных и двумерных случайных величин
- 2. Характеристики двумерной случайной величины (ξ, η) –
- 3. КовариацияОпределение. Ковариацией случайной величины (ξ, η) называется
- 4. Ковариация Величины ξ,η называются некоррелированными при cov(ξ,
- 5. Коэффициент корреляцииОпределение. Коэффициентом корреляции между случайными величинами ξ, η называется число
- 6. Свойства коэффициента корреляции1. │ρξη│≤ 1.2. Если ξ,η
- 7. Смысл коэффициента корреляции Коэффициент корреляции есть мера
- 8. Пример: ρ = +0,9
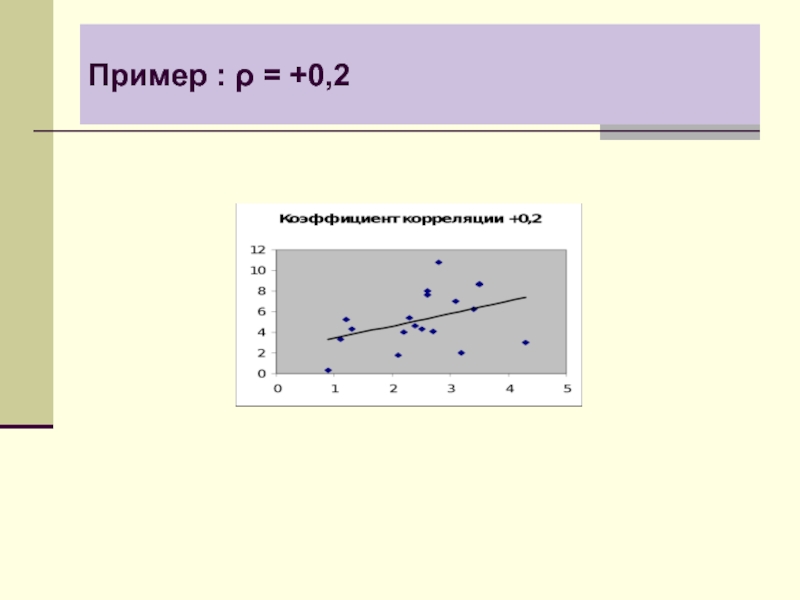
- 9. Пример : ρ = +0,2
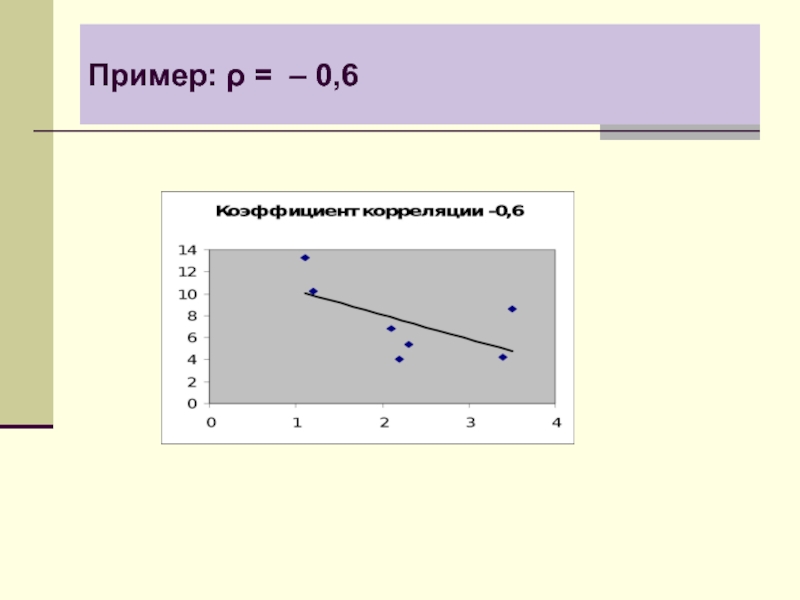
- 10. Пример: ρ = – 0,6
- 11. Линейная зависимость Проблема: найти функцию, описывающую линейную зависимость (уравнение прямой).
- 12. Уравнение линейной регрессииОпределение. Уравнением линейной регрессии η
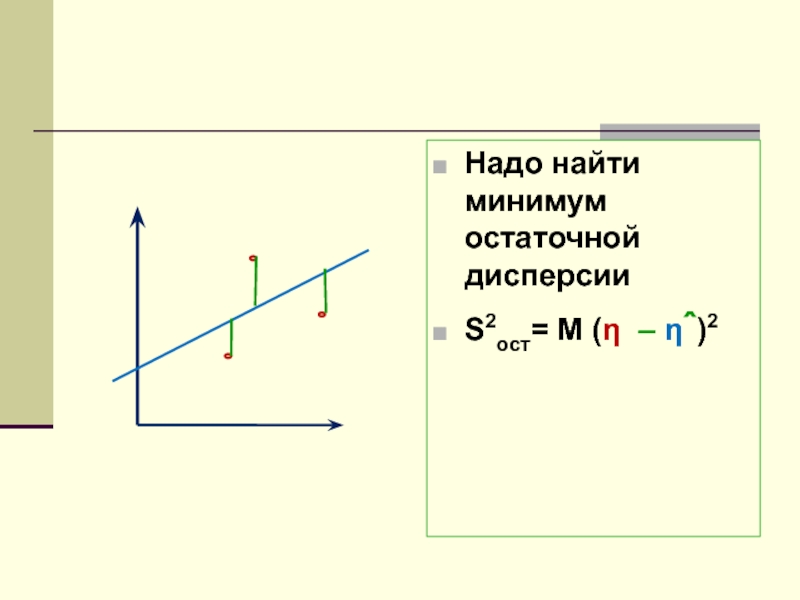
- 13. Надо найти минимум остаточной дисперсии S2ост= M (η – ηˆ)2
- 14. Нахождение коэффициентов уравнения линейной регрессииS2ост = M[η
- 15. (Mη – aMξ – b) – постоянная
- 16. Поскольку M(η – Mη)2 = Dη =
- 17. S2ост – функция переменных a и
- 18. S2ост = σ2η+ a2σ2ξ + (Mη
- 19. Подставим a = ρ∙ση/σξ, b = Mη
- 20. Замечание Коэффициент уравнения линейной регрессии ρ∙ση/σξ можно
- 21. Остаточная дисперсияНайдем значение S2ост = M(η –
- 22. σ2η + (ρ∙ση)2 – 2 ρ2∙ση2 =
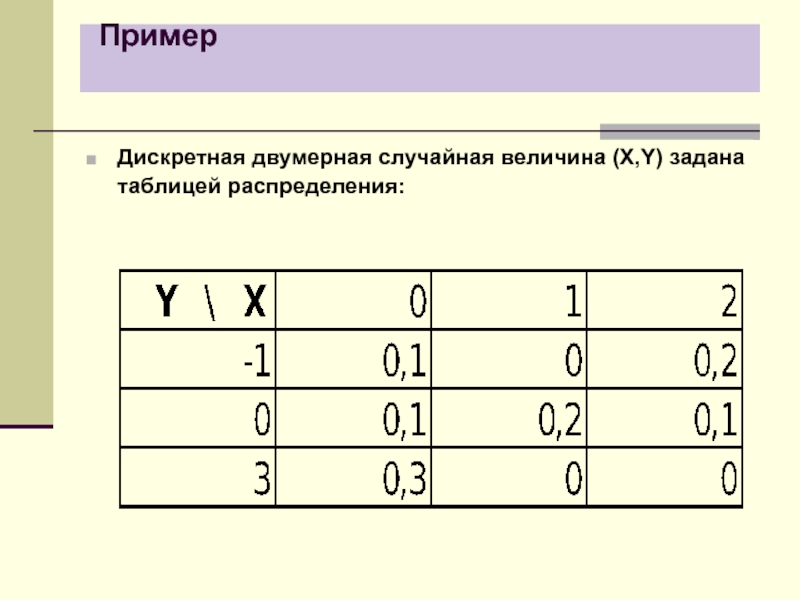
- 23. Пример Дискретная двумерная случайная величина (X,Y) задана таблицей распределения:
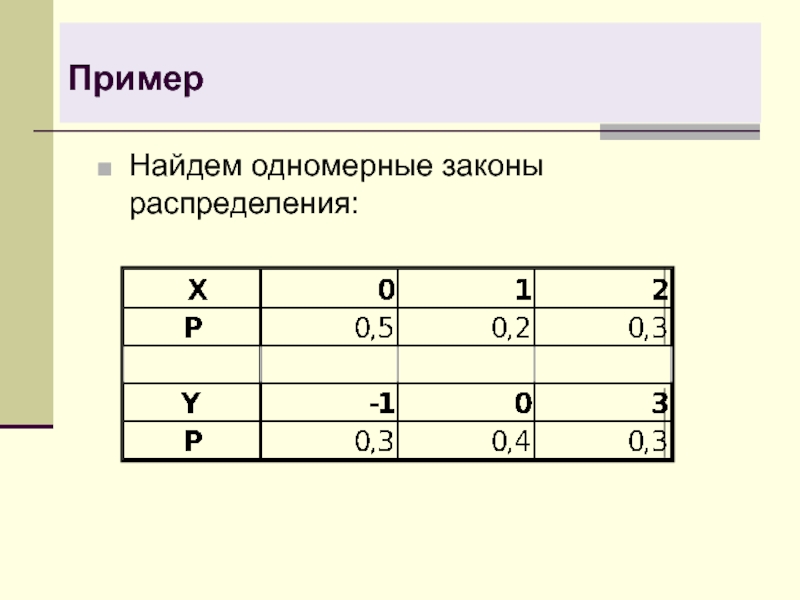
- 24. Пример Найдем одномерные законы распределения:
- 25. Пример Вычислим числовые характеристики.MX = 0∙0,5 +
- 26. ПримерНайдем ковариацию: cov(ξ, η) = M(ξ∙η) –
- 27. Коэффициент корреляции
- 28. Уравнение линейной регрессииЗапишем уравнение линейной регрессии Y
- 29. Остаточная дисперсияYˆ – 0,6 = – 1,16(X
- 30. График линейной регрессииYˆ= – 1,16X + 1,53.
- 31. Нелинейная зависимость Проблема: найти функцию, описывающую нелинейную зависимость.
- 32. Условные распределенияПусть (ξ, η) – двумерная случайная
- 33. Условные распределения η при разных значениях ξ.
- 34. Способы нахождения условных распределений в дискретном случаеРассмотрим
- 35. Пример Найдем условный закон распределения Y/X = 0:
- 36. Действительно, P(Y = –1/X = 0) =
- 37. Найдем другие условные законы.Условный закон распределения Y/X = 1:
- 38. Такой закон распределения записывается в виде ряда распределения
- 39. Условный закон распределения Y/X=2:
- 40. Условное математическое ожиданиеОпределение. Условным математическим ожиданием случайной
- 41. ЗамечаниеУсловное математическое ожидание обладает свойствами математического ожидания .
- 42. Условное математическое ожидание
- 43. Вспомним предыдущий пример. Найдем условное матожидание Y/X=0:M(Y/X=0)= (–1)∙1/5 + 0∙1/5 + 3∙3/5 = 8/5
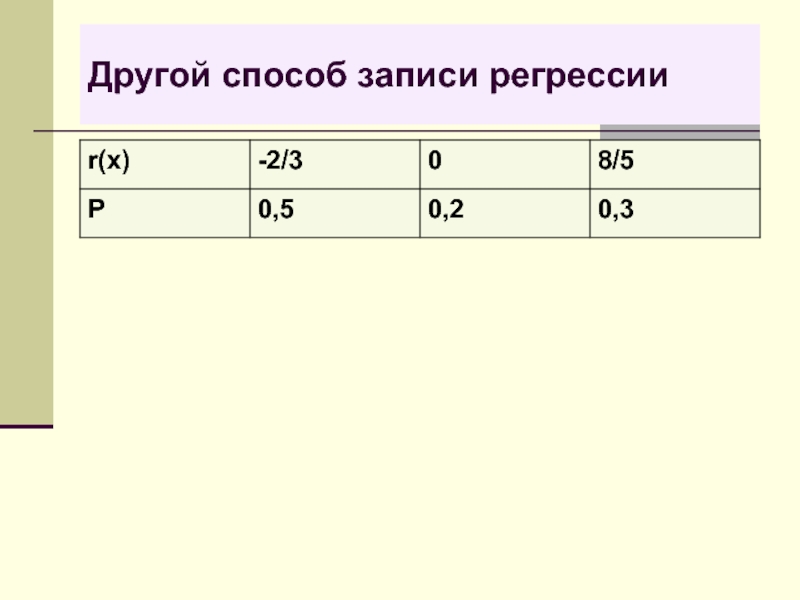
- 44. Аналогично, условные матожидания M(Y/X=1) = 0∙1 =0,M(Y/X=2) = (–1)∙2/3 + 0∙1/3 = –2/3.
- 45. РегрессияОпределение. Регрессией η на ξ называется случайная
- 46. Пример В условиях предыдущего примера регрессия Y на X равна:
- 47. Другой способ записи регрессии
- 48. Слайд 48
- 49. Корреляционное отношениеОпределение. Корреляционным отношением η на ξ называется числовая характеристика, равная
- 50. Свойства корреляционного отношения1. 0 ≤ θ2η,ξ ≤
- 51. Смысл: корреляционное отношение измеряет силу зависимости η от ξ
- 52. Пример.Чтобы найти θ2YX, надо сначала найти MY
- 53. MY = ( –1)∙0,3 + 0∙0,4 +
- 54. Смысл полученного числа: корреляционное отношение измеряет силу
- 55. Условные распределенияОпределение. Условной функцией распределения случайной величины
- 56. Условная плотностьОпределение. Если условная функция распределения случайной
- 57. Обозначается условная плотностьfη/ξ = x(y)(плотность распределения η
- 58. Нахождение условной функции распределенияУсловная функция распределения случайной величины η при условии, что ξ = x
- 59. Нахождение условной плотности распределенияУсловная плотность распределения сл. в. η при условии, что ξ = x
- 60. Поскольку
- 61. Числовые характеристики многомерных случайных величинОпределение. Ковариационной матрицей
- 62. Ковариационная матрица К
- 63. Корреляционная матрица RНаряду с ковариационной матрицей рассматривают
- 64. Уравнение множественной линейной регрессии Рассмотрим случайные величины
- 65. Определение. Уравнением линейной регрессии ξ0 на ξ1, ξ2 , …, ξn называется уравнение
- 66. Здесь bi (i =1,…, n) – параметры, минимизирующие остаточную дисперсию
- 67. Минимизируя остаточную дисперсию, получаем, что
- 68. Остаточная дисперсия Здесь и далее через
- 69. Частный коэффициент корреляцииЧастный коэффициент корреляции используется как
- 70. Множественный (сводный) коэффициент корреляцииВыражает зависимость между ξ0
- 71. Скачать презентанцию
Характеристики двумерной случайной величины (ξ, η) – это характеристики одномерных величин ξ и η, и характеристики связи между ними. Дальше мы будем рассматривать именно статистическую связь, которая называется корреляцией. Вначале рассмотрим
Слайды и текст этой презентации
Слайд 1Теория вероятностей и математическая статистика
Числовые характеристики
двумерных и многомерных случайных
величин
Слайд 2Характеристики двумерной случайной величины (ξ, η) – это характеристики одномерных
величин ξ и η, и характеристики связи между ними. Дальше
мы будем рассматривать именно статистическую связь, которая называется корреляцией. Вначале рассмотрим линейную связь и ее характеристики – ковариацию, коэффициент корреляции, уравнение линейной регрессии, остаточную дисперсию.Характеристики двумерной случайной величины
Слайд 3Ковариация
Определение. Ковариацией случайной величины (ξ, η) называется центральный смешанный момент
второго порядка
Kξ,η = cov(ξ, η) = M[(ξ – Mξ)∙(η
– Mη)]. Ковариация есть мера линейной зависимости между ξ, η.
Слайд 4Ковариация
Величины ξ,η называются
некоррелированными при cov(ξ, η) = 0,
положительно коррелированными при cov(ξ, η) > 0,
отрицательно коррелированными при
cov(ξ, η) < 0.Для вычисления ковариации часто используют формулу
cov(ξ, η) = M(ξ∙η) – M ξ∙M η.
Слайд 5Коэффициент корреляции
Определение. Коэффициентом корреляции между случайными
величинами ξ, η называется
число
Слайд 6Свойства коэффициента корреляции
1. │ρξη│≤ 1.
2. Если ξ,η независимы, то ρξη=
0.
Если │ρξη│=1, то ξ, η линейно зависимы,
то
есть существуют такие a и b, что ξ = aη + b.
Слайд 7Смысл коэффициента корреляции
Коэффициент корреляции есть мера линейной зависимости между
ξ, η.
Его модуль указывает на силу линейной связи
(чем ближе к 1, тем сильнее), а знак указывает на направление связи.
Слайд 11Линейная зависимость
Проблема: найти функцию, описывающую линейную зависимость (уравнение прямой).
Слайд 12Уравнение линейной регрессии
Определение. Уравнением линейной регрессии η на ξ называется
уравнение
ηˆ = aξ + b, параметры которого минимизируют остаточную
дисперсию S2ост= M (η – ηˆ)2 = M(η – (aξ + b))2.
Смысл. Уравнение линейной регрессии η на ξ
выражает линейную зависимость η от ξ.
Слайд 14Нахождение коэффициентов уравнения линейной регрессии
S2ост = M[η – (aξ+b)]2 =
M[(η – Mη) – a(ξ – Mξ) + (Mη –
aMξ – b)]2 =M(η – Mη)2 + a2M(ξ – M ξ)2 + M[(Mη – aMξ – b)]2 –
2aM[(η – Mη)(ξ – Mξ)] + 2M[(η – Mη)(Mη – aMξ – b)] – 2aM[(ξ – Mξ)(Mη – aMξ – b)].
![Нахождение коэффициентов уравнения линейной регрессииS2ост = M[η – (aξ+b)]2 = M[(η – Mη) – a(ξ – Mξ)](/img/thumbs/1efa18ab590ae4e56d3c928ed71d8a5b-800x.jpg "Числовые характеристики одномерных и двумерных случайных величин Нахождение коэффициентов уравнения линейной регрессииS2ост = M[η – (aξ+b)]2 = M[(η")
Слайд 15
(Mη – aMξ – b) – постоянная величина, ее можно
вынести за знак матожидания.
M(η – Mη) = Mη – M[Mη]
= Mη – Mη = 0, M(ξ – M ξ) = 0
Подставляя, получаем:
S2ост = M(η – Mη)2 + a2M(ξ – M ξ)2 +
+ (Mη – aMξ – b)2 – 2aM[(η – Mη)(ξ – Mξ)].
Слайд 16
Поскольку M(η – Mη)2 = Dη = σ2η,
M(ξ –
M ξ)2 = Dξ = σ2ξ,M[(ξ – Mξ)∙(η – Mη)] = cov(ξ,η) = ρσξση, то
S2ост = σ2η+ a2σ2ξ + (Mη – aMξ – b)2 – 2a ρσξση.
Слайд 17
S2ост – функция переменных a и b, надо найти
min S2ост , то есть найти значения
a и b,
при которых достигается минимум.Найдем производные от S2ост по a и b.
Слайд 18 S2ост = σ2η+ a2σ2ξ + (Mη – aMξ – b)2
– 2a ρσξση.
(S2ост)'b= –2(Mη – aMξ – b) = 0
(S2ост)'a = 2aσ2ξ – 2Mξ (Mη – aMξ – b) –
–2ρσξση = 0
Из первого уравнения находим:
b = Mη – aMξ.
Подставляя во второе, получаем:
a = ρ∙ση/σξ.
Слайд 19
Подставим
a = ρ∙ση/σξ, b = Mη – aMξ
В уравнение
ηˆ= aξ+b.
Получим:
ηˆ= ρ∙ση/σξ∙ ξ + Mη – ρ∙ση/σξ ∙
Mξ, или
Слайд 20Замечание
Коэффициент уравнения линейной регрессии ρ∙ση/σξ можно записать в виде:
ρ∙ση/σξ =
cov(ξ,η)/σ2ξ.
Тогда уравнение линейной регрессии примет вид:
Слайд 21Остаточная дисперсия
Найдем значение S2ост = M(η – ηˆ)2 = M(η
– (aξ+b))2. Для этого подставим полученные значения a и b.
S2ост
= M(η – (aξ + b))2 = M(η – (aξ + b))2=M[η – Mη – ρ∙ση/σξ(ξ – M ξ)]2 = M(η –Mη)2 +
(ρ∙ση/σξ)2 M(ξ – M ξ)]2 –2 ρ∙ση/σξ M[(ξ – Mξ)∙
(η – Mη)] = σ2η+ (ρ∙ση/σξ)2σ2ξ –
2 ρ∙ση/σξ ∙ ρσξση =
Слайд 22σ2η + (ρ∙ση)2 – 2 ρ2∙ση2 = σ2η – ρ2∙ση2
=
= σ2η (1 – ρ2).
Смысл: остаточная дисперсия выражает ошибку приближения
при замене η на ηˆ= aξ+b.Остаточная дисперсия
Слайд 25Пример
Вычислим числовые характеристики.
MX = 0∙0,5 + 1∙0,2 + 2∙0,3
= 0,8.
DX = 02∙0,5 + 12∙0,2 + 22∙0,3 – 0,82
= 0,76.MY = ( –1)∙0,3 + 0∙0,4 + 3∙0,3 = 0,6.
DY = ( –1)2∙0,3 + 02∙0,4 + 32∙0,3 – 0,62 = 2,64.
M(XY) = ( –1)∙2∙0,2 = – 0,4.
Слайд 26Пример
Найдем ковариацию:
cov(ξ, η) = M(ξ∙η) – M ξ∙ M
η.
В наших обозначениях
cov(X, Y) = M(X∙Y) – MX∙ MY.
cov(X,Y) =
– 0,4 – 0,8∙0,6 = – 0,88.Величины X,Y отрицательно коррелированы.
Слайд 28Уравнение линейной регрессии
Запишем уравнение линейной регрессии Y на X.
Подставим MX
= 0,8, DX = 0,76, MY = 0,6. cov(X,Y) =
– 0,88.Yˆ – 0,6 = – 0,88/0,76∙(X – 0,8).
Слайд 29Остаточная дисперсия
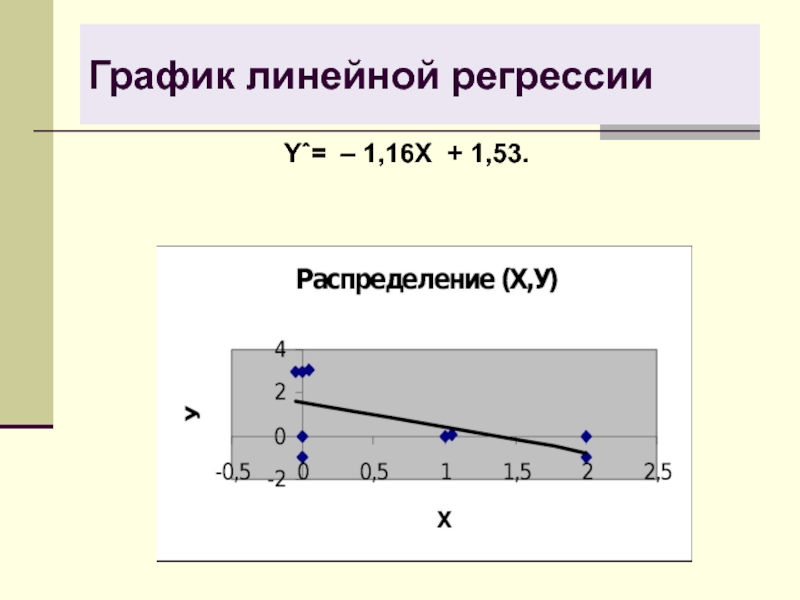
Yˆ – 0,6 = – 1,16(X – 0,8).
Yˆ= –
1,16X +1,53.
Найдем остаточную дисперсию:
S2ост.= σ2Y (1 – ρ2).
S2ост.= 2,64∙(1 –0,642)
≈ 1,56.
Слайд 32Условные распределения
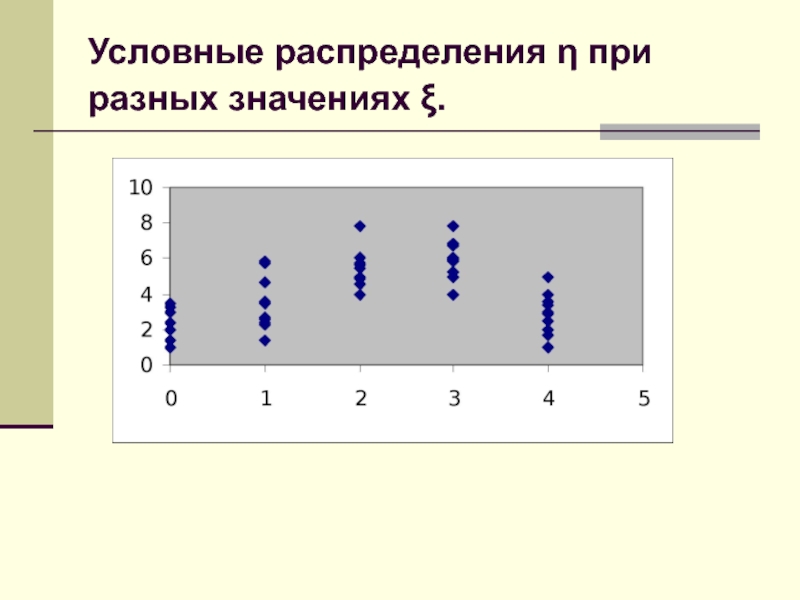
Пусть (ξ, η) – двумерная случайная величина. Рассмотрим распределение
η при условии, что ξ = x. Оно называется условным.
Слайд 34Способы нахождения условных распределений в дискретном случае
Рассмотрим пример. Пусть дискретная
двумерная случайная величина (X, Y) задана таблицей:
Слайд 36Действительно,
P(Y = –1/X = 0) = P(Y = –1,
X = 0)/P(X = 0) т.к. по формуле условной вероятности,
P(A/B) = P(AB)/P(B).
P(Y = –1,X = 0) =0,1
P(X =0) = 0,5.
Отсюда P(Y= –1/X = 0) = 0,1: 0,5 = 1/5.
Аналогично P(Y = 0/X=0) = 0,1: 0,5 = 1/5,
P(Y = 3/X = 0) = 0,3: 0,5 =3/5.
Слайд 40Условное математическое ожидание
Определение. Условным математическим ожиданием случайной
величины η при
условии, что ξ = x,
называется математическое ожидание, найденное
с помощью условного закона распределения.Обозначение: M(η/ξ = x).
Слайд 43Вспомним предыдущий пример.
Найдем условное матожидание Y/X=0:
M(Y/X=0)= (–1)∙1/5 + 0∙1/5
+ 3∙3/5 = 8/5
Слайд 45Регрессия
Определение. Регрессией η на ξ называется случайная величина r(ξ), равная
при каждом x условному математическому ожиданию случайной величины η при
условии, что ξ = x. Определение. Линией регрессии называется линия y = r(x), гдеr(x) = M(η/ξ = x).
Слайд 49Корреляционное отношение
Определение. Корреляционным отношением η на ξ называется числовая характеристика,
равная
Слайд 50Свойства корреляционного отношения
1. 0 ≤ θ2η,ξ ≤ 1.
2. θ2η,ξ ≥
ρ2.
3. θ2η,ξ = ρ2 ↔ r(ξ) = aξ+b (т.е., линейная
зав–ть).4. θ2η,ξ = 0 ↔ r(ξ) = Mη (r(ξ)=const, нет связи).
5. θ2η,ξ = 1 ↔ η = r(ξ) (т.е., функц–я зав–ть).
Слайд 52Пример.
Чтобы найти θ2YX, надо сначала найти MY и DY.
Мы их
недавно находили с помощью одномерного закона.
Слайд 54Смысл полученного числа: корреляционное отношение измеряет силу зависимости Y от
X.
Чем ближе к 1, тем связь сильнее, чем ближе к
0, тем слабее.Напоминание: корреляционное отношение принимает значения от 0 до 1.
Если надо найти θ2XY, а не θ2YX , то в формуле надо поменять местами X и Y.
Слайд 55Условные распределения
Определение. Условной функцией распределения случайной величины
η при
условии, что ξ = x, называется
Fη/ξ = x = P(η
< y/ξ = x).
Слайд 56Условная плотность
Определение. Если условная функция распределения случайной величины η при
условии, что ξ = x, непрерывна, то производная от нее
называется условной плотностью распределения случайной величины η при условии, что ξ = x.
Слайд 57
Обозначается условная плотность
fη/ξ = x(y)
(плотность распределения η в точке y
при условии, что ξ = x).
Слайд 58 Нахождение условной функции распределения
Условная функция распределения случайной величины η
при условии, что ξ = x
Слайд 59Нахождение условной плотности распределения
Условная плотность распределения сл. в. η при
условии, что ξ = x
Слайд 61Числовые характеристики многомерных случайных величин
Определение. Ковариационной матрицей случайных величин ξ1,
ξ2 , …, ξn называется матрица K размерности n x
n с элементами aij, равными ковариациям cov(ξi, ξj) = kij.K= (kij)n x n = (cov(ξi, ξj)) n x n
Слайд 63Корреляционная матрица R
Наряду с ковариационной матрицей рассматривают и матрицу R,
составленную из коэффициентов корреляции ρij = ρ(ξi, ξj).
Слайд 64Уравнение множественной линейной регрессии
Рассмотрим случайные величины
ξ0 ξ1, ξ2
, …, ξn
с математическими ожиданиями Mξi = ai,
с
дисперсиями Dξi = σ2i, i = 0,1,…, n,
и c корреляционной матрицей R размерности (n+1) х (n+1).
Слайд 68Остаточная дисперсия
Здесь и далее через Rij обозначено алгебраическое
дополнение элемента aij матрицы R, а через |R| – определитель
матрицы R.Остаточная дисперсия равна
Слайд 69Частный коэффициент корреляции
Частный коэффициент корреляции используется как мера линейной
зависимости между двумя какими –либо случайными величинами за вычетом влияния
остальных случайных величин.
Слайд 70Множественный (сводный) коэффициент корреляции
Выражает зависимость между ξ0 и всей совокупностью
ξ1, ξ2 , … , ξn .
