Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что изучает топология?
Содержание
- 1. Что изучает топология?
- 2. История топологииЛ. ЭйлерГ. В. ЛейбницИ. Б. Листинг«Под
- 3. История топологии Ф. ХаусдорфП. С. АлександровА. ПуанкареП. С. УрысонЛ. Э. Ян Брауэр
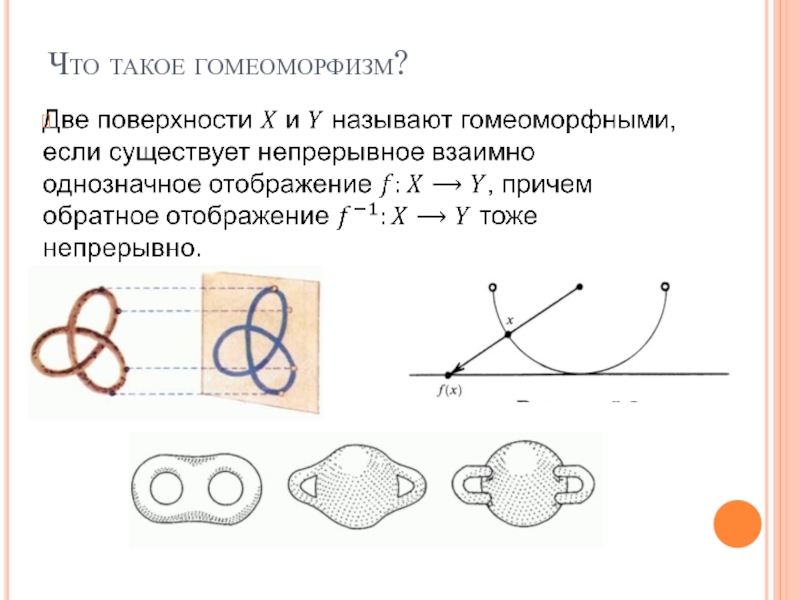
- 4. Что такое гомеоморфизм?
- 5. Лист (лента) МебиусаА. Ф. Мебиус
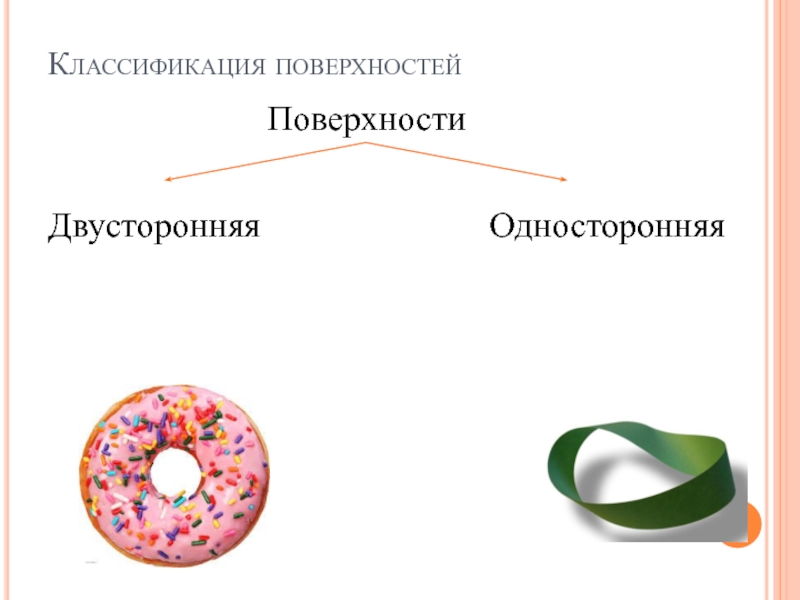
- 6. Классификация поверхностейПоверхностиОдносторонняяДвусторонняя
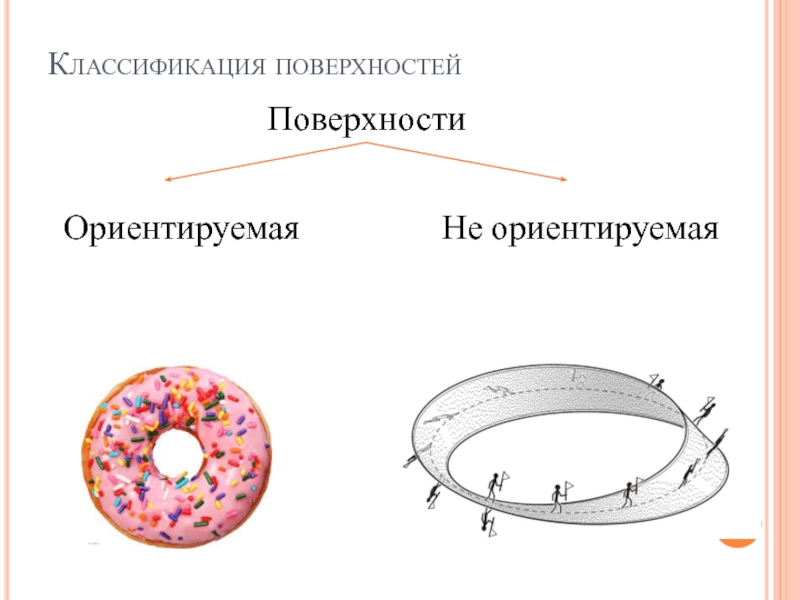
- 7. Классификация поверхностейПоверхностиОриентируемаяНе ориентируемая
- 8. Классификация поверхностейПоверхностиС краемБез края
- 9. Классификация поверхностейКомпактная поверхность – такая поверхность, которая
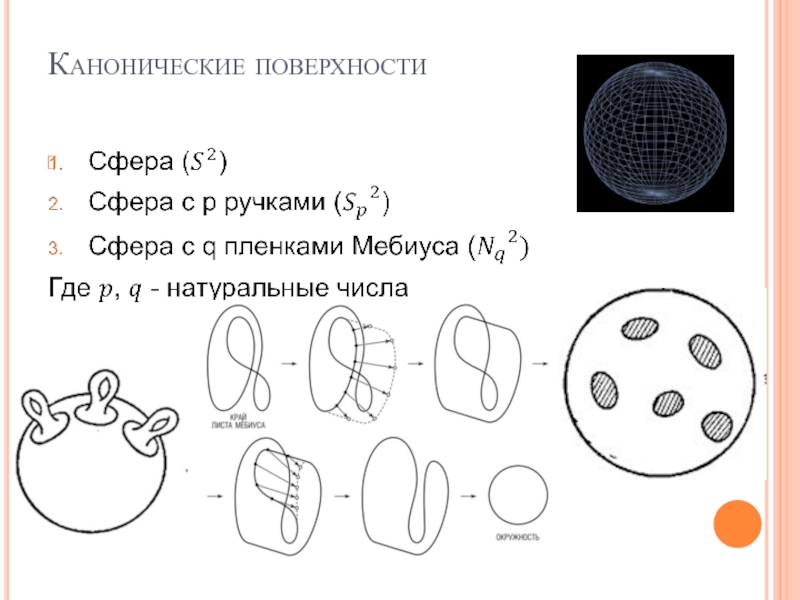
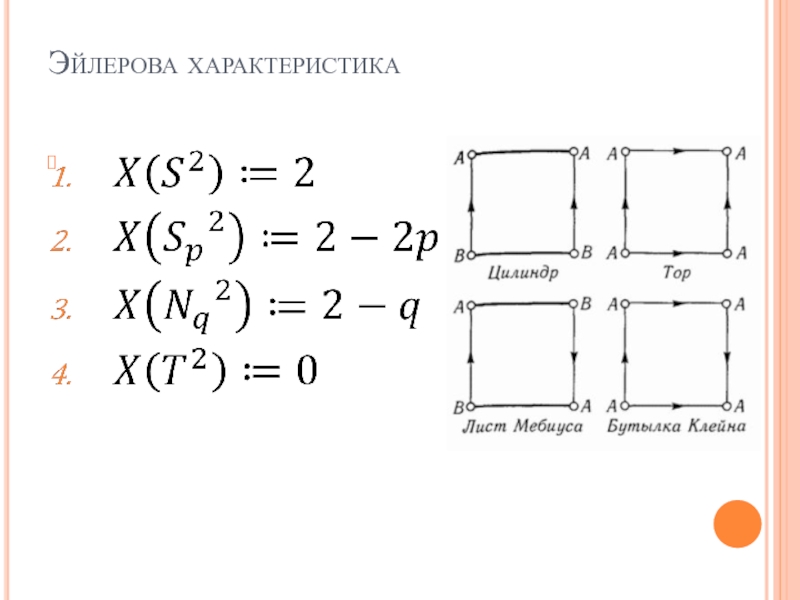
- 10. Канонические поверхности
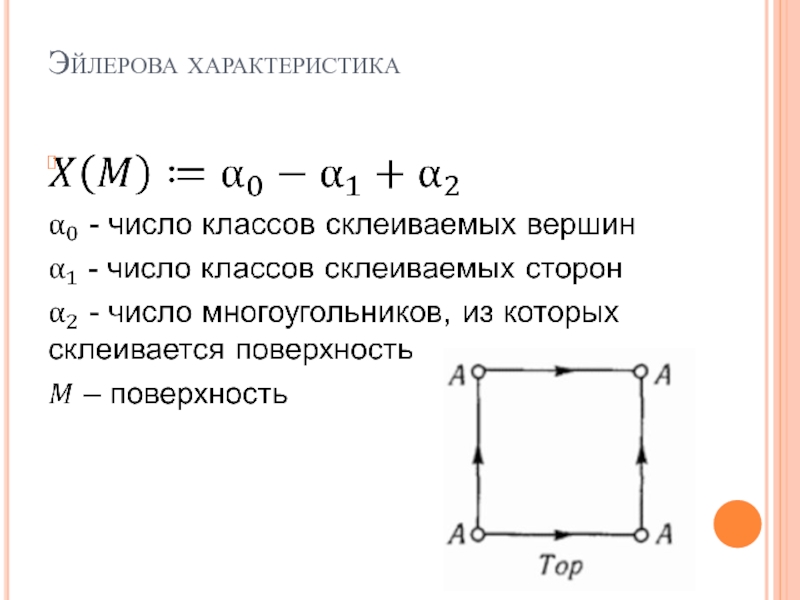
- 11. Эйлерова характеристика
- 12. Эйлерова характеристика
- 13. Топологические инвариантыТопологический инвариант - это такая характеристика пространства, которая сохраняется при гомеоморфизме.Топологические инварианты:Эйлерова характеристикаКомпактностьОриентируемость
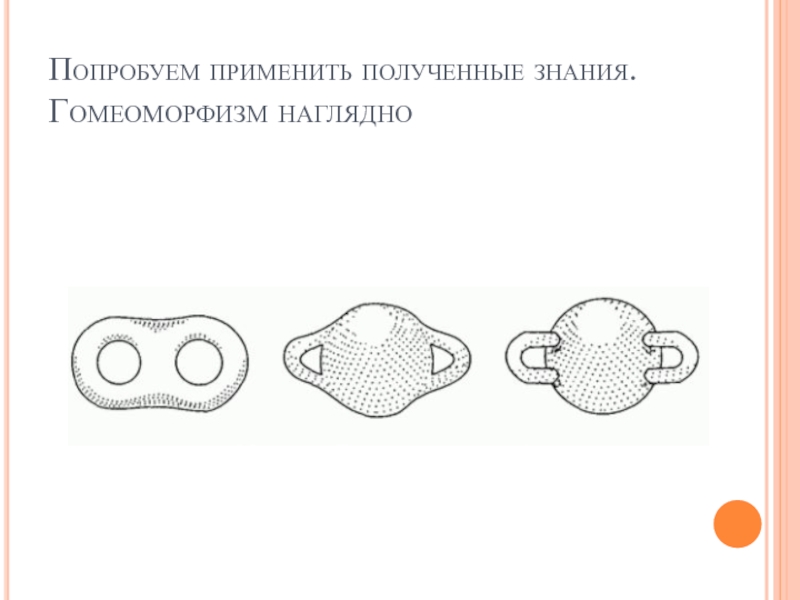
- 14. Попробуем применить полученные знания. Гомеоморфизм наглядно
- 15. Попробуем применить полученные знания拓扑
- 16. Попробуем применить полученные знания
- 17. Попробуем применить полученные знания
- 18. Русский алфавит
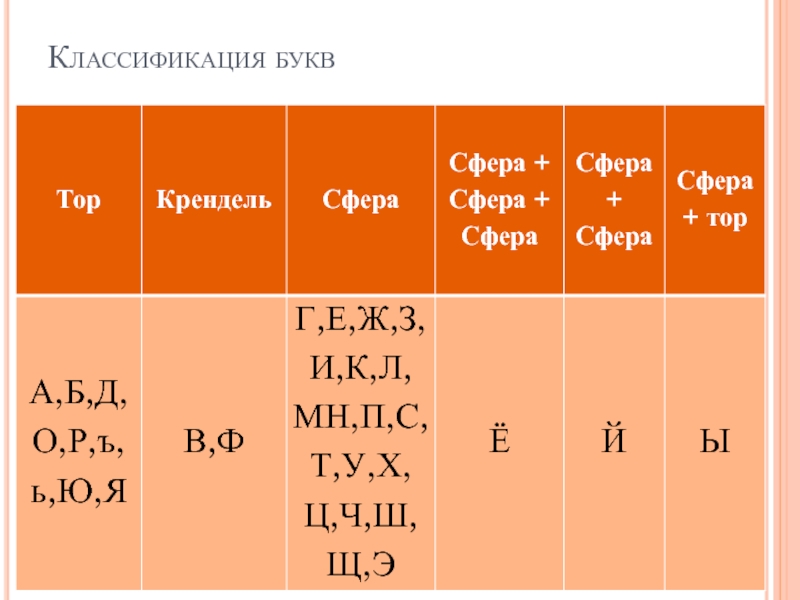
- 19. Классификация букв
- 20. Характеристика полученных поверхностей
- 21. Скачать презентанцию
История топологииЛ. ЭйлерГ. В. ЛейбницИ. Б. Листинг«Под топологией будем понимать учение о модальных отношениях пространственных образов — или о законах связности, взаимного положения и следования точек, линий, поверхностей, тел и их
Слайды и текст этой презентации
Слайд 9Классификация поверхностей
Компактная поверхность – такая поверхность, которая замкнута (содержит все
свои предельные точки) и ограничена по размеру.
Слайд 13Топологические инварианты
Топологический инвариант - это такая характеристика пространства, которая сохраняется при гомеоморфизме.
Топологические
инварианты:
Эйлерова характеристика
Компактность
Ориентируемость
