Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Декартова система координат в пространстве и на плоскости. Полярная система
Содержание
- 1. Декартова система координат в пространстве и на плоскости. Полярная система
- 2. Опр.: Упорядоченные координатные оси, не лежащие в
- 3. Слайд 3
- 4. Слайд 4
- 5. Примеры1) Задать точку плоскости А (-1; 1)
- 6. Прямые на плоскостиПрямая на координатной плоскости может
- 7. Таким образом Ах + Ву + С
- 8. Слайд 8
- 9. Угол между прямымиПусть прямые заданы уравнениемА1х +
- 10. y L2L10хУсловия параллельности и
- 11. Примеры1. Определить острый угол между прямыми
- 12. Линии второго порядка на плоскости
- 13. Линии второго порядка на плоскости.Общее уравнение линии
- 14. Каноническое
- 15. Слайд 15
- 16. Выразим
- 17. Свойства эллипсаЭллипс – ограниченная кривая второго порядка.Эллипс
- 18. 5. Прямые
- 19. ГиперболаОпределение: Гиперболой называется множество
- 20. Слайд 20
- 21. Выразим r1 =
- 22. Слайд 22
- 23. Свойства гиперболыГипербола – неограниченная кривая второго порядка.Гипербола
- 24. Примеры: Дана гипербола 16х2 – 9у2 =
- 25. ПараболаОпределение: параболой называется множество
- 26. Слайд 26
- 27. Выразим
- 28. Свойства параболыПарабола – неограниченная кривая второго порядка,
- 29. Пример: Установить, что
- 30. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Декартова система координат в пространстве и на плоскости. Полярная
система координат на плоскости.
Прямая на плоскости.
Кривые второго порядка
Слайд 2Опр.: Упорядоченные координатные оси, не лежащие в одной плоскости и
имеющую одну общую точку, называются косоугольной системой координат в пространстве.
Если координатные оси взаимно перпендикулярны, то косоугольную систему координат называют прямоугольной системой координат Декарта в пространстве и обозначают хуz.Опр.: Множество упорядоченных троек чисел в избранной системе координат называется трехмерным пространством.
Слайд 3
z
z1
P(х1; у1; z1)
у1 у
х1
х
Элементы системы координат:
координатные плоскости Оху, Оуz, Охz;
оси координат: Ох – ось абсцисс, Оу – ось ординат; Оz – ось аппликат.
Точка О – начало координат;
упорядоченная тройка чисел (х; у; z) – координаты произвольной точки Р.
у
у1 Р(х1; у1)
0 х1 х
Частным случаем является система координат на плоскости, например координатная плоскость Оху.
Слайд 4
у
Р (х1; у1)
r
φ
0 А х
Точка на плоскости может быть задана полярной системой координат, при этом положение точки Р описывается углом поворота положительной полуоси Ох против часовой стрелки до положения луча ОР и расстоянием точки Р от начала координат.
Из Δ АРО, где
, имеем:
Слайд 5Примеры
1) Задать точку плоскости А (-1; 1) в полярных координатах.
Решение.
r=
Таким образом А
2) Задать точку плоскости В (0,5; π/4) в декартовых координатах.
Решение.
х1=0,5cosπ/6 =0,5
у1=0,5sin π/6= 0,5·1/2 .
Таким образом В (0,25 ; 0,25)
Слайд 6Прямые на плоскости
Прямая на координатной плоскости может быть получена в
результате пересечения произвольной плоскости
Ах + Ву + Сz + D = 0 и координатной плоскости.Составим уравнение прямой, принадлежащей, например, плоскости хОу. Эта прямая определяется системой двух уравнений:
Слайд 7Таким образом Ах + Ву + С = 0 (*)
– общее уравнение прямой на координатной плоскости, причем
(А; В) является нормальным вектором этой прямой.n L
Опр.: геометрическое место точек, удовлетворяющее уравнению (*), называется прямой.
у
b - уравнение прямой в отрезках на осях
а
0 L у
L - уравнение прямой,
М1(х1;у1) М2(х2;у2) проходящей через две точки
Слайд 8
у
L
b
φ
0 х
L: у= kх+b, где k= tgφ – уравнение прямой с угловым коэффициентом;
L: у – у1= k (х – х1) – уравнение прямой с угловым коэффициентом, проходящей через т. М (х1; у1).
Слайд 9Угол между прямыми
Пусть прямые заданы уравнением
А1х + В1у + С1
=0 и А2х + В2у + С2 =0
Угол между этими
прямыми найдем из формулы:Если прямые заданы уравнением с угловыми коэффициентами, то угол между ними находим по формуле:
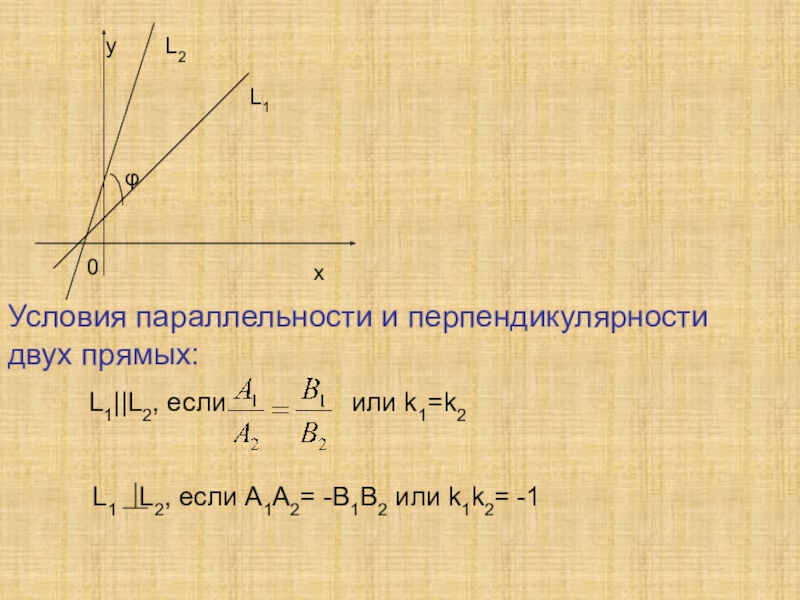
Слайд 10y L2
L1
0
х
Условия параллельности и перпендикулярности двух прямых:
L1||L2, если
или k1=k2L1 L2, если А1А2= -В1В2 или k1k2= -1
φ
Слайд 11Примеры
1. Определить острый угол между прямыми у = 3х
+ 1 и у = -2х – 5.
Решение. Полагая k1= 3 и k2= -2 и применяя формулу (1), получимtg = -2–3/1+(-2)3= -5/-5= 1, т.е. = /4= 0,785 рад.
2. Показать, что прямые 7х + 3у – 5 = 0 и 14х + 6у + 1 = 0 параллельны.
Решение. Приведя уравнение каждой прямой к виду с угловым коэффициентом, получаем:
у= -7/3х+5/3 и у= -7/3х+1/14.
Угловые коэффициенты этих прямых равны: k1= k2= -7/3, т. е. прямые параллеьны.
3. Даны вершины треугольника А (-5; 0), В (-3; -2) и С (-7; 6). Найти уравнения высот треугольника AD, BN и CM.
Решение. По формуле (4) найдем угловой коэффициент стороны ВС:
kВС= 6+2/-7–(-3)= 8/-4= -2.
В силу перпендикулярности прямых AD и BC kAD= -1/kВС, т. е. kAD= ½.
Уравнение высоты, проведенной из вершины А будет иметь вид:
у–0= ½(х+5) или х–2у+5= 0.
Слайд 13Линии второго порядка на плоскости.
Общее уравнение линии второго порядка на
плоскости:
а11х2 + а22у2 + 2а12ху + а10х + а20у +
а00 = 0, где а211 + а212 + а222 ≠ 0, т. е. хотя бы одно из чисел а11,а12,а22 не равно нулю.Окружностью называется геометрическое место точек плоскости, равноудаленных от данной точки (центра).
Слайд 14
Каноническое уравнение окружности с
центром в точке М(х0;у0) и радиусом R.
Уравнение
окружности с центром в начале координатЭллипсом называется геометрическое место точек, сумма расстояний каждой из которых до двух заданных точек этой же плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
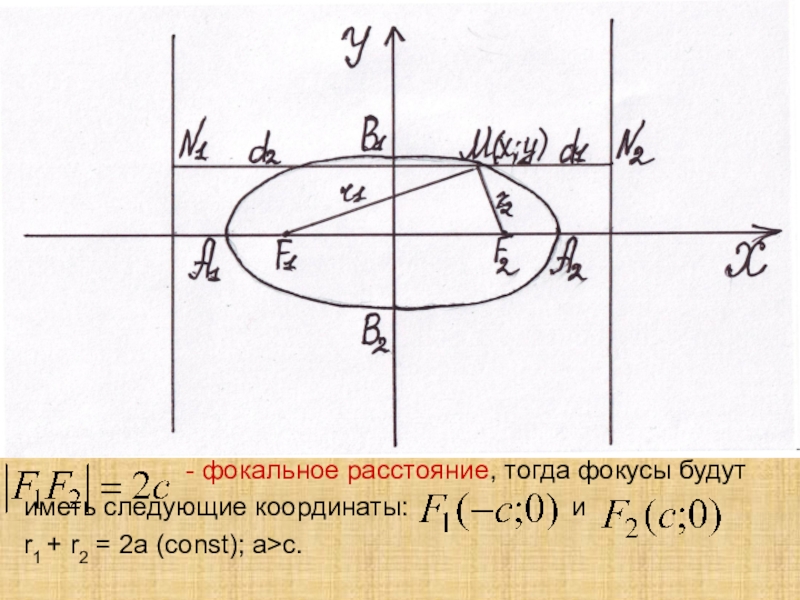
Слайд 15
иметь следующие координаты: и
r1 + r2 = 2а (const); a>c.
Слайд 16
Выразим r1 =
, r2 = , тогда
аналитическое уравнение эллипса примет вид:
Обозначив , получим каноническое уравнение эллипса:
Слайд 17Свойства эллипса
Эллипс – ограниченная кривая второго порядка.
Эллипс имеет вертикальную и
горизонтальную оси симметрии, а так же центр симметрии.
А1 А2 - большая ось (ОА1 - полуось), В1 В2 – малая ось (ОВ1 - полуось).А1, А2, В1, В2 - вершины эллипса, причем
- называется эксцентриситетом эллипса,
,т.е. 0< <1;
- характеризует: “вытянутость эллипса, т.е. отклонение от окружности”.
=1, значит x2+y2 = a2, где а – радиус окружности
Слайд 18
5. Прямые
называются директрисами
(направляющими)
т.о. имеем:
, где d1=Пример:
Дан эллипс найти полуоси, эксцентриситет,
уравнения директрис.
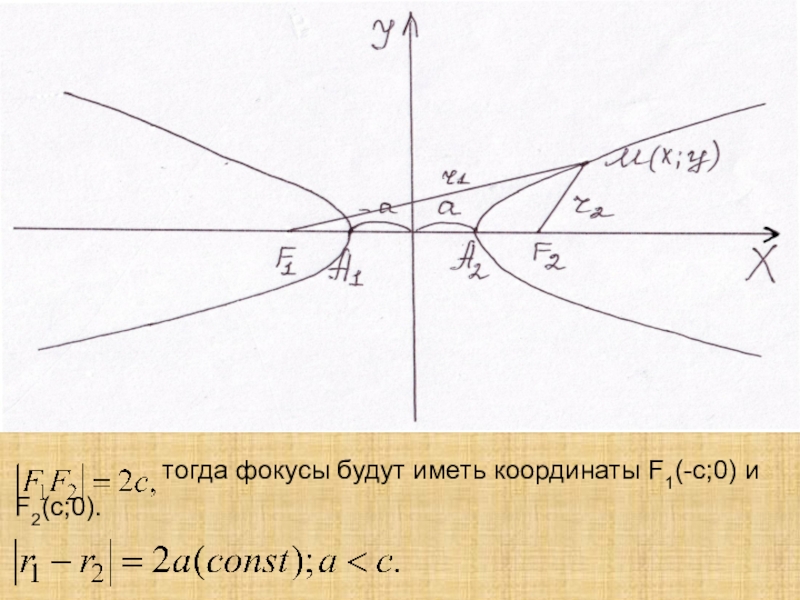
Слайд 19
Гипербола
Определение: Гиперболой называется множество точек плоскости, модуль разности расстояний каждой
из которых до двух данных точек, называемых фокусами, есть величина
постоянная.Слайд 21
Выразим r1 =
, r2 =
, тогдааналитическое уравнение гиперболы примет вид:
Обозначив , получим каноническое уравнение гиперболы:
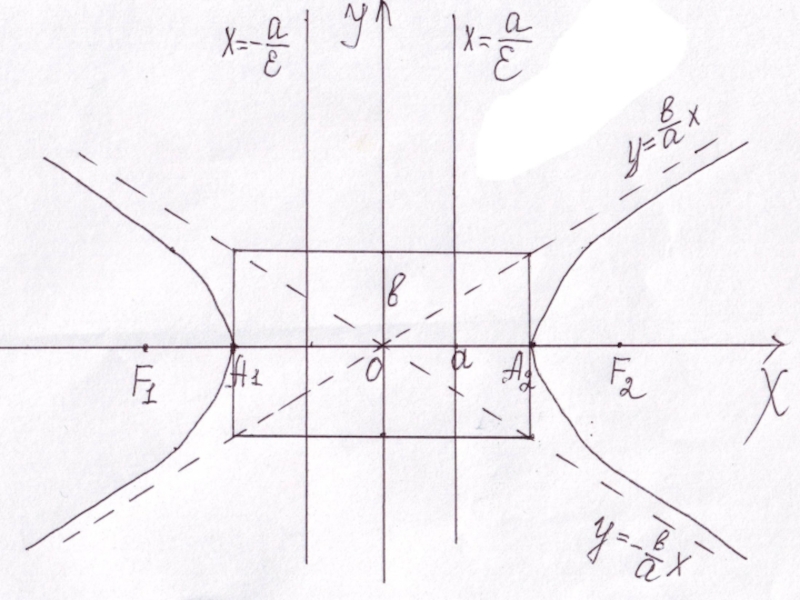
Слайд 23Свойства гиперболы
Гипербола – неограниченная кривая второго порядка.
Гипербола обладает центральной симметрией.
А1,
А2 – действительные вершины гиперболы; ось 2а – действительная, 2b
– мнимая.Прямоугольник со сторонами 2а и 2b называется основным прямоугольником гиперболы.
Гипербола имеет две асимптоты:
Эксцентриситет гиперболы:
причем
Прямые - называется директрисами гиперболы
причем
Слайд 24Примеры: Дана гипербола 16х2 – 9у2 = 144, найти: полуоси
а и b; фокусы; эксцентриситет; уравнения асимптот; уравнения директрис.
16х2 –
9у2 = 1441.
2.
3.
4.
5.
Слайд 25
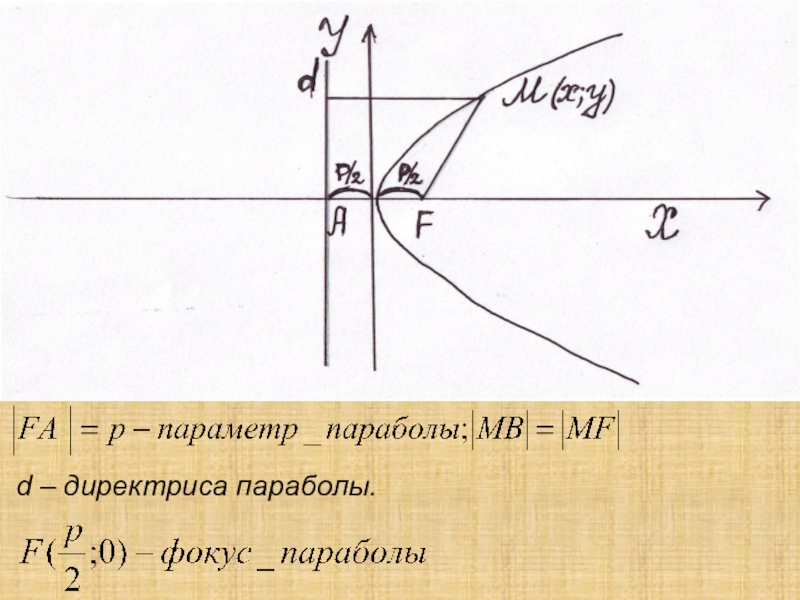
Парабола
Определение: параболой называется множество точек плоскости, равноудаленных от фиксированной точки
плоскости(фокус F) и фиксированной прямой (директриса d).
Слайд 27
Выразим
тогда
аналитическое уравнение параболы примет вид:
таким образом получим каноническое уравнение параболы:
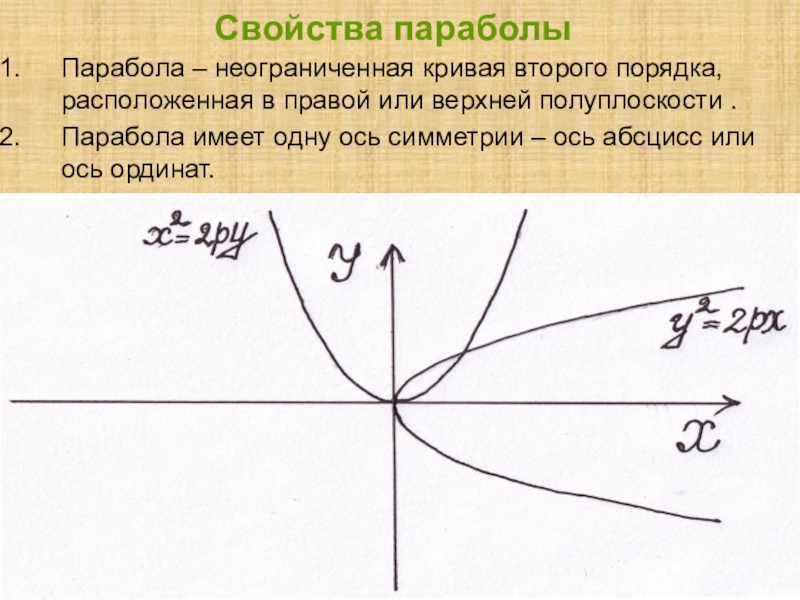
Слайд 28Свойства параболы
Парабола – неограниченная кривая второго порядка, расположенная в правой
или верхней полуплоскости .
Парабола имеет одну ось симметрии – ось
абсцисс или ось ординат.Слайд 29
Пример: Установить, что уравнение у2 =
4х – 8 определяет параболу, и найти координаты ее вершины
А, величину параметра р и уравнение директрисы.у2 = 4х – 8
Представим уравнение в каноническом виде: у2 = 4(х - 2)
вершина параболы смещена вдоль оси ОХ вправо на две единицы.
А(2;0) – координаты вершины параболы.
2р = 4 р = 2 – параметр параболы.
3. - уравнение директрисы параболы.