Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Декартово произведение множеств
Содержание
- 1. Декартово произведение множеств
- 2. Декартово произведение множествСвоё название декартово произведение получило
- 3. Декартовым произведением множеств A и B называется
- 4. Пример декартова произведения конечных множествЗадайте декартово произведение
- 5. Затем составим все пары, первое место в
- 6. Составим все пары, первое место в которых
- 7. Пример декартова произведения конечных множеств
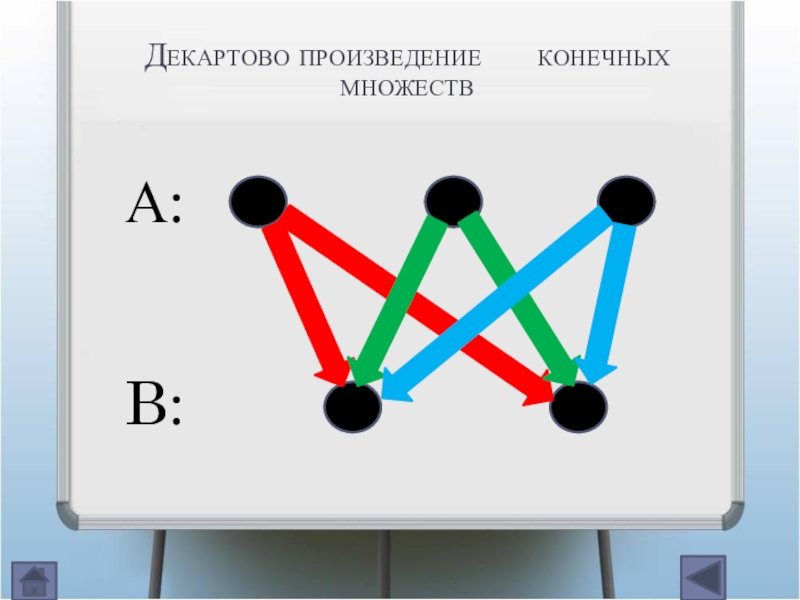
- 8. Декартово произведение конечных множествА:B:
- 9. Декартово произведение двух конечных множеств В
- 10. Задание декартова произведения конечных множеств таблицей(
- 11. Задание декартова произведения числовых
- 12. Пример задания декартова произведения числовых множеств
- 13. Пример задания декартова произведения конечных множеств геометрически xy421-13-301
- 14. Скачать презентанцию
Декартово произведение множествСвоё название декартово произведение получило в честь выдающегося французского математика, философа, физика и естествоиспытателя Рене Декарта. Рене Декарт (1596-1650)
Слайды и текст этой презентации
Слайд 2Декартово произведение множеств
Своё название декартово произведение получило в честь выдающегося
французского математика, философа, физика и естествоиспытателя
(1596-1650)
Слайд 3Декартовым произведением множеств A и B называется множество АхВ, состоящее
из всех упорядоченных пар вида (а,b), при этом первым элементом
пары является элемент множества А, а вторым – элемент множества В.Декартово произведение множеств
Слайд 4Пример декартова произведения конечных множеств
Задайте декартово произведение множеств A и
B перечислением элементов, если
.
Решение:
Сначала составим все пары, первое
место в которых займет первый элемент множества A – 1, а на втором последовательно окажется каждый из элементов множества В. Таких пар получим две: 
Слайд 5Затем составим все пары, первое место в которых займет второй
элемент множества A – 3, а на втором последовательно окажется
каждый из элементов множества В. Таких пар получим две:.
Пример декартова произведения конечных множеств
Слайд 6Составим все пары, первое место в которых займет третий –
последний элемент множества A – 5, а на втором последовательно
окажется каждый из элементов множества В. Таких пар получим две:Пример декартова произведения конечных множеств
Слайд 9 Декартово произведение двух конечных множеств В и А в
ряде случаев удобно задавать таблицей.
Для этого элементы множества В
размещают в первом столбце таблицы, элементы множества А – в первой строке и формируют пары: элемент строки – элемент столбца.Пример:
Задайте декартово произведение множеств B и A таблицей, если
Задание декартова произведения конечных множеств таблицей
Слайд 10
Задание декартова произведения конечных множеств таблицей
( , )
(
, )
( , )
( , )
( , )
( , )
1
1
3
5
5
3
1
3
5
Слайд 11
Задание декартова
произведения числовых множеств геометрически
Декартово произведение двух числовых множеств A и B можно задать
геометрически в прямоугольной декартовой системе координат на плоскости.Для этого элементы множества A откладываются по оси абсцисс, а элементы множества B – по оси ординат.
Элементами собственно декартова произведения являются точки плоскости.
Слайд 12Пример задания декартова
произведения числовых множеств геометрически
Изобразите геометрически декартово произведение
множеств A и B, если:
