Слайд 1
Diagnostika lineárního regresního modelu
Слайд 2Postup tvorby lineárního modelu
1. Návrh modelu (začíná se od nejjednoduššího)
2.
Předběžná analýza dat (sleduje se proměnlivost jednotlivých proměnných a možné
párové vztahy)
3. Odhadování parametrů modelu (metodou MNČ)
4. Regresní diagnostika (identifikace odlehlých pozorování a ověření předpokladů MNČ)
5. Konstrukce zpřesněného modelu
6. Zhodnocení kvality modelu (testy, regresní diagnostika nového modelu)
Слайд 3Regresní diagnostika
Regresní diagnostika obsahuje postupy k posouzení:
kvality dat
kvality
modelu
splnění předpokladů
Слайд 4Diagnostika kvality dat
Vlivné body lze rozdělit do tří skupin
Hrubé chyby
Body
s vysokým vlivem
Zdánlivě vlivné body
Слайд 5Diagnostika kvality dat
Podle polohy rozlišujeme vlivné body na:
vybočující pozorování
(outliers)
extrémy (leverage points)
Ve statistických programech se na rozdíl od
odborné statistické literatury nerozlišují vybočující
pozorování a extrémy a obecně se hovoří od
odlehlých pozorováních
Слайд 6Diagnostika kvality dat
Nejednoduší grafické vyjádření odlehlých pozorování
Graf predikovaných reziduí
Osa y – klasická rezidua
Osa x – predikovaná rezidua
O - vybočující bod (leží na
přímce nebo v její blízkosti,
ale daleko od ostáních bodů)
E – extrémní bod (leží mimo přímku)
Слайд 7Diagnostika kvality dat
Projekční matice H (hat matrix)
Studentizovaná rezidua
Odlehlost neznamená
vlivnost!!!
Слайд 8Diagnostika kvality dat
Míra vlivu kombinace proměnných x a y
Cookova D
veličina
Míra vlivu jednotlivých pozorování
Welshova-Kuhova vzdálenost DFFIT(-i).
Слайд 9Diagnostika kvality dat
Požadavky kladené na rezidua
reziduum ei = yi
– yi´
mají nulovou střední hodnotu E(ei) = 0 a konstantní rozptyl E(ei2) = 2
jsou nekorelované (jsou nezávislé)
jsou náhodná mají normální rozdělení
Слайд 10Diagnostika kvality dat
Rezidua jsou nekorelované - posouzení podmínky
o nezávislosti
reziduí se provádí pomoci
Durbin-Watsonova statistiky. Vzájemná závislost
reziduí může naznačovat autokorelaci
Слайд 11Diagnostika kvality dat
Posouzení podmínky o náhodnosti reziduí se
provádí pomocí
testů normality reziduí nebo
graficky.
Слайд 12Diagnostika kvality dat
Grafická analýza reziduí
Pokud se v diagnostických grafech reziduí
objeví
tvar „mraku“ bodů, je detekována správnost metody
nejmenších čtverců.
Слайд 13Diagnostika kvality dat
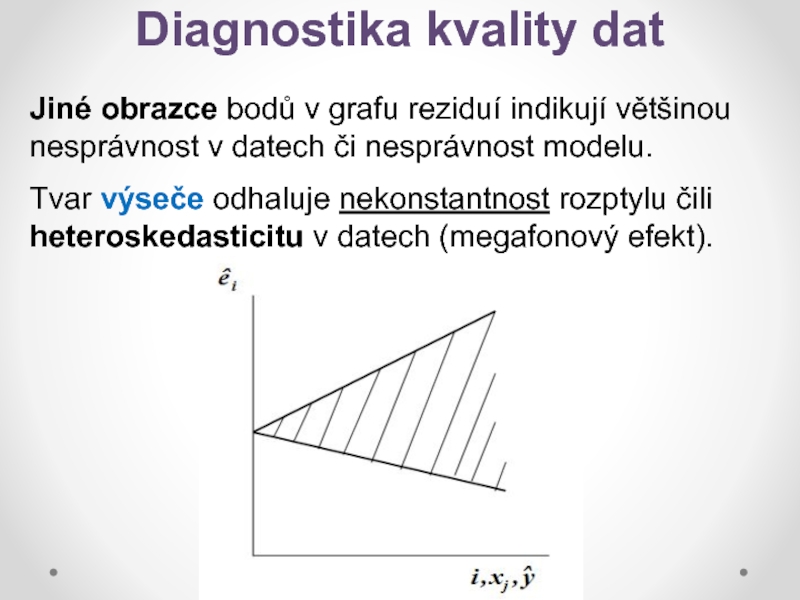
Jiné obrazce bodů v grafu reziduí indikují většinou
nesprávnost v datech či nesprávnost modelu.
Tvar výseče odhaluje nekonstantnost rozptylu
čili
heteroskedasticitu v datech (megafonový efekt).
Слайд 14Diagnostika kvality dat
Tvar pásu indikuje chybu ve výpočtu nebo se
jedná o
důsledek vybočujících hodnot. Může také indikovat
chybný výpočet
a nebo to, že kdy v regresní modelu
chybí absolutní člen.
Слайд 15Diagnostika kvality dat
Nelineární tvar ukazuje na nesprávně navržený
model.
Analýza
reziduí a její grafické znázornění, nám také
může sloužit k první
identifikaci odlehlých pozorování.
Слайд 16 Diagnostika kvality modelu
Kritika a analýza modelu jako celku
Kvalitu regresního
modelu lze posoudit graficky či numericky.
V případě jedné
vysvětlující proměnné x přímo z rozptylového grafu závislosti y na x.
Numericky s využitím klasických testů (např.:F- test, t-test) a postupů regresní diagnostiky.
Слайд 17Diagnostika metody odhadů
Splnění předpokladů MNČ
Regresní parametry mohou teoreticky nabývat
jakýchkoli hodnot.
Regresní model je lineární v parametrech.
Nezávislé proměnné x jsou skutečně
vzájemně
nezávislé.
Podmíněný rozptyl D(y/x) = 2 je konstantní.
Náhodné chyby i mají nulovou střední hodnotu, konečný a konstantní rozptyl a jsou nekorelované.
Слайд 18Literatura
[1] M. Meloun, J. Militký: Statistické zpracování experimentálních dat, Plus
Praha 1994, (1. vydání), East Publishing Praha 1998 (2. vydání),
Academia Praha 2004 (3. vydání).
[2] M. Meloun, J. Militký: Statistické zpracování experimentálních dat - Sbírka úloh, Univerzita Pardubice 1996.
[3] ADSTAT 1.25, 2.0 a verze 3.0, TriloByte Statistical Software Pardubice, 1992, 1993, 1999.
[4] M. Meloun, J. Militký: Kompendium statistického zpracování experimentálních dat, Academia Praha 2002 (1. vydání), Academia Praha 2006 (2. rozšířené vydání).
![Literatura[1] M. Meloun, J. Militký: Statistické zpracování experimentálních dat, Plus Praha 1994, (1. vydání), East Publishing Praha](/img/thumbs/1b0f778a659f03eaa092375051375c0c-800x.jpg "Diagnostika lineárního regresního modelu Literatura[1] M. Meloun, J. Militký: Statistické zpracování experimentálních dat, Plus Praha")
