TheSlide.ru

Диаметр, радиус и центр графа

Содержание

1. Диаметр, радиус и центр графа
2. Задан граф
3. Ввод данныхint main() { int G[100][100], //
4. Oпределение длины кратчайших путейint r[100]={0}, // 0
5. Определение. Диаметр связного графа – максимально возможное расстояние
6. Определение диаметра графаint D=0;For(i=1; i
7. Определение. Радиус связного графа – максимально возможное расстояние
8. Определение радиуса графаint Rad=0;for(i=1; i
9. Определение. Центр графа – вершина, максимальное расстояние от
10. Определение центра графа// Rad – радиус графаfor(i=1; i
11. Скачать презентанцию

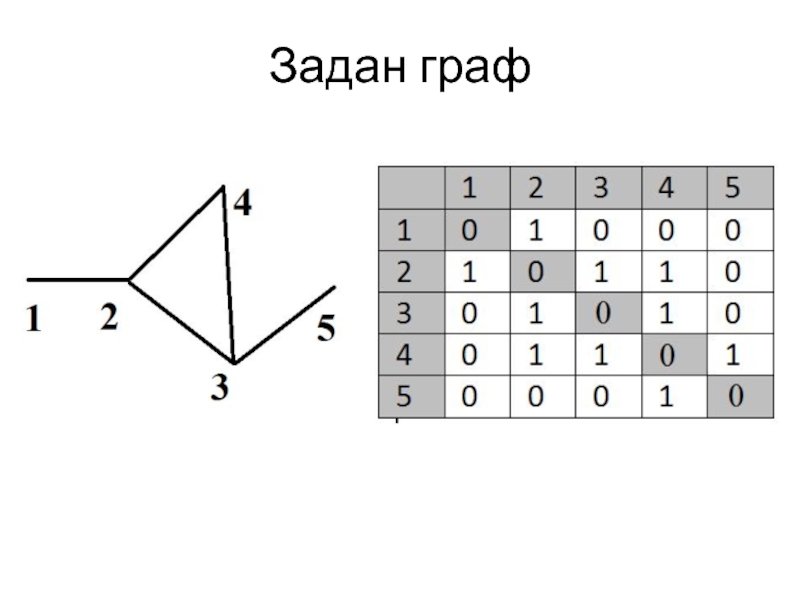
Задан граф

Главная
Разное
Диаметр, радиус и центр графа

Слайды и текст этой презентации

Слайд 1Диаметр, радиус и центр графа
Старший преподаватель
кафедры теоретической кибернетики
Хадиев Р.М.
КАЗАНСКИЙ ФЕДЕРАЛЬНЫЙ

УНИВЕРСИТЕТ

Диаметр, радиус и центр графаСтарший преподавателькафедры теоретической кибернетикиХадиев Р.М.КАЗАНСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

Слайд 2Задан граф

Задан граф

Слайд 3Ввод данных
int main() {
int G[100][100], // граф транспортной сети

R[100][100], // минимальные расстояния

// между вершинами
I,j,n, // n – число вершин
cin >> n;
for (i=1; i<=n; i++)
for (j=1; j<=n; j++)
cin >> G[i][j];

Ввод данныхint main() { int G[100][100], // граф транспортной сети R[100][100], // минимальные расстояния

Слайд 4Oпределение длины кратчайших путей
int r[100]={0}, // 0 – расстояние не

определено
ob[100], // обработанные вершины
For (n_p=1; n_p

{
Int a=1, // вершина из ob , которая обрабатывается
p=2; // пустое место для записи новых вершин
r[n_p]=1; // кратчайший путь в n_p – 1
ob[1]=n_p; //
while a

for (i=0; i if (G[i][ob[a]]==1 & r[i]==0) { //необработанные вершины
r[i]=r[ob[a]]+1;
ob[++p]=I;
}
a++;
}
for(i=1; i<=n; i++) R(n_p][i]=r[i];
}

Oпределение длины кратчайших путейint r[100]={0}, // 0 – расстояние не определено ob[100], // обработанные вершиныFor

Слайд 5Определение. Диаметр связного графа – максимально возможное расстояние между двумя его вершинами. Для

решения задачи строим матрицу кратчайших расстояний между вершинами
Диаметр - 3

Определение. Диаметр связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим матрицу

Слайд 6Определение диаметра графа
int D=0;
For(i=1; i

D:= max(D,R[i][j]);
Cout

Определение диаметра графаint D=0;For(i=1; i

Слайд 7Определение. Радиус связного графа – максимально возможное расстояние между двумя его вершинами. Для

решения задачи строим матрицу кратчайших расстояний между вершинами
Диаметр - 3

Определение. Радиус связного графа – максимально возможное расстояние между двумя его вершинами. Для решения задачи строим матрицу

Слайд 8Определение радиуса графа
int Rad=0;
for(i=1; i

i

Rad=min(Rad,M);
}
cout << “Радиус графа = “ << Rad;

Определение радиуса графаint Rad=0;for(i=1; i

Слайд 9Определение. Центр графа – вершина, максимальное расстояние от которого до любой другой

вершины является наименьшим из всех возможных. Для решения задачи строим

матрицу кратчайших расстояний между вершинами

Центр - 2,3 или 4

Определение. Центр графа – вершина, максимальное расстояние от которого до любой другой вершины является наименьшим из всех возможных.

Слайд 10Определение центра графа
// Rad – радиус графа
for(i=1; i

int M=0;
for(i=1; i

(Rad==M
cout << “Центр графа = “ << i;
}

Определение центра графа// Rad – радиус графаfor(i=1; i

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей